
Hypothesis-Driven and Game-Theoretic Sensor Tasking
SURI IRT 3 Year 1 Report
Assistant Professor Zachary Sunberg
University of Colorado Boulder
Fall, 2024
Autonomous Decision and Control Laboratory

-
Algorithmic Contributions
- Scalable algorithms for partially observable Markov decision processes (POMDPs)
- Motion planning with safety guarantees
- Game theoretic algorithms
-
Theoretical Contributions
- Particle POMDP approximation bounds
-
Applications
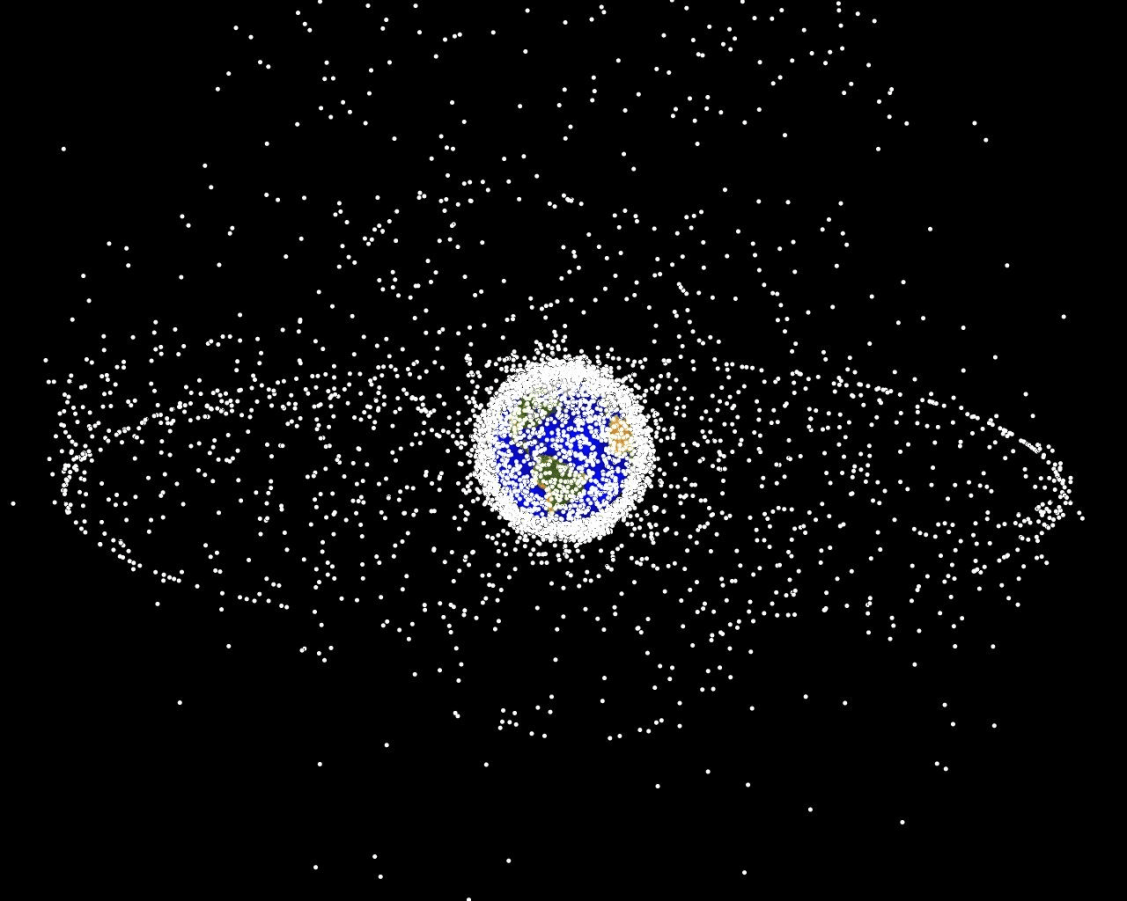
- Space Domain Awareness
- Autonomous Driving
- Autonomous Aerial Scientific Missions
- Search and Rescue
- Space Exploration
- Ecology
-
Open Source Software
- POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students









Postdoc





Outline
- Accomplishments for this year
- Hypothesis-driven sensor tasking
- General hypothesis-driven planning
- LLM-based hypothesis-to-model translation
- Partially observable stochastic games
- Future Plans
- Integrating filtering and planning into user-facing software
- Realistic space POSGs
Deliverable
2 Papers Submitted to AAMAS
SURI Team within ADCL


Dr. Ofer Dagan
Postdoctoral Associate
Tyler Becker
Doctoral Student
1. Hypothesis-driven sensor tasking
Problem formulation
Object Of Interest (OOI)
Example Hypotheses:
- OOI deployed a solar panel
- OOI performed a station-keeping maneuver
- OOI is attempting to rendezvous with a specific object
Given an existing catalog maintenance plan and a set of hypotheses, how do we task sensors to gather data to distinguish between hypotheses with a minimum disruption?








Baseline Integer Linear Program (ILP) for catalog maintenance
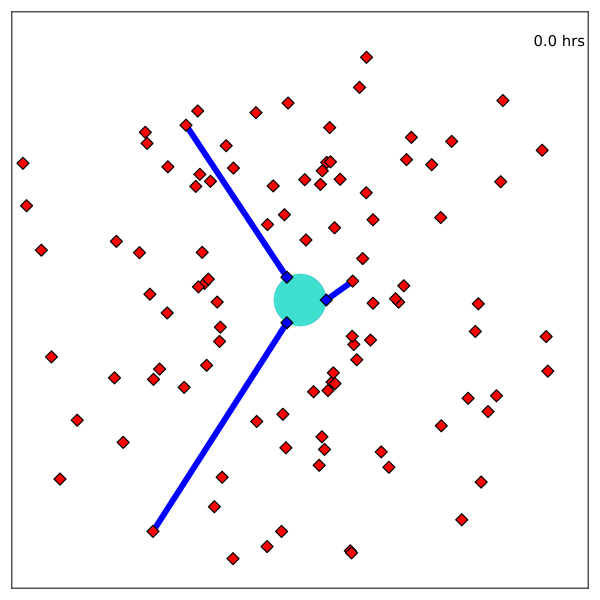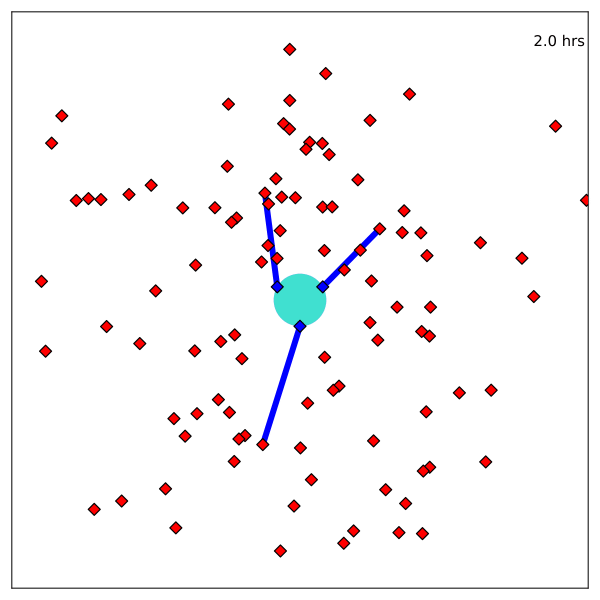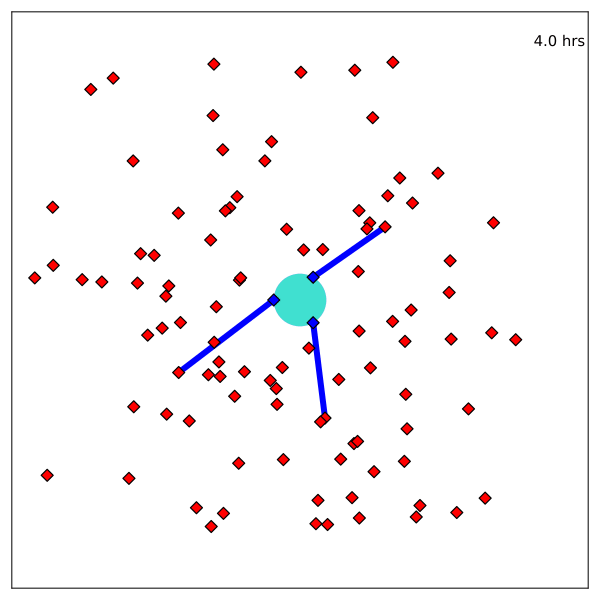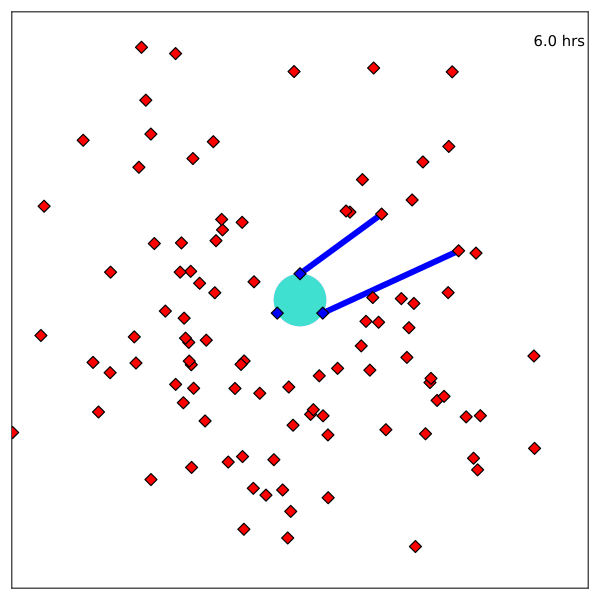
\(X_{ijt}\): Observer \(j\) measures object \(i\) at time \(t\)
\(O_{ijt}\): Observability
\(r\): Measurements of least-measured
Optimization Formulation
Optimal control in the information space
- State: "Belief" distribution of hypothesis probabilities: \(b_H\)
- Controls: Sensor tasking modifications: \(a\)
- Dynamics: Bayesian belief update \(b'_H = \tau(b_H, a, o)\)
- Cost: \(-\rho(b_H)\) e.g. entropy
Solve with Monte Carlo Tree Search

Resulting Plans
Implementation
Website: https://www.cu-adcl.org/SURI/
Fulfills "Basic Tasking Algorithm Implementation" deliverable requirement
2. General Hypothesis-driven Planning
Markov Decision Process (MDP)
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward

Aleatory
\[\underset{\pi:\, \mathcal{S} \to \mathcal{A}}{\text{maximize}} \quad \text{E}\left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right]\]

\(s = (x, y, z, \dot{x}, \dot{y}, \dot{z})\)
\(\mathcal{S} = \mathbb{R}^6\)
Additional state variables:
- Orientation
- fuel
- configuration
- intention
Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward
- \(\mathcal{O}\) - Observation space
- \(\mathcal{Z}(o \mid s, a, s')\) - Observation probability distribution

\(s = (x, y, z, \dot{x}, \dot{y}, \dot{z})\)
\(\mathcal{S} = \mathbb{R}^6\)
Additional state variables:
- Orientation
- fuel
- configuration
- intention
Belief MDP
- BMDP state space = belief space (\(\Delta(\mathcal{S})\))
- BMDP transition dynamics = belief dynamics, \(b' = \tau(b, a, o)\), defined with \(\mathcal{T}\) and \(\mathcal{Z}\)
- \(\mathcal{A}\) - Action space
- Belief-dependent reward \(\rho(b, a)\)

\(s = (x, y, z, \dot{x}, \dot{y}, \dot{z})\)
\(\mathcal{S} = \mathbb{R}^6\)
Additional state variables:
- Orientation
- fuel
- configuration
- intention

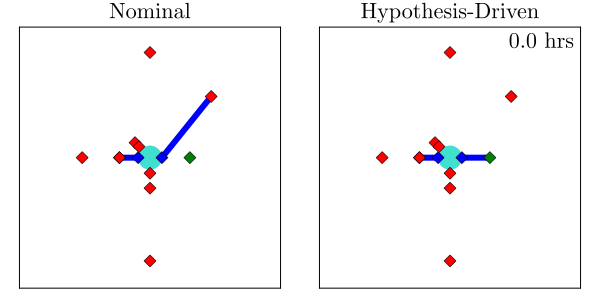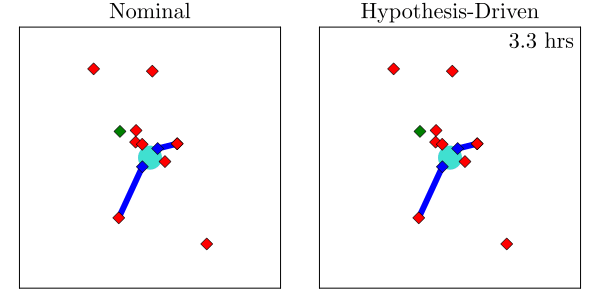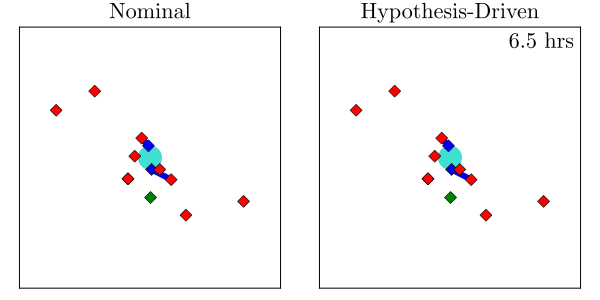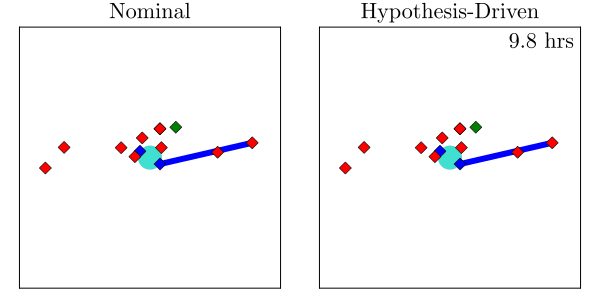
Hypothesis-Driven Belief MDP Formulation

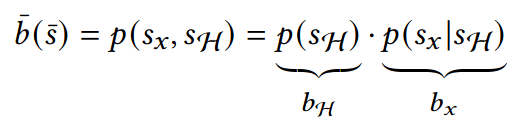
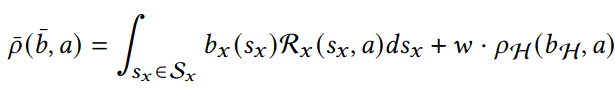
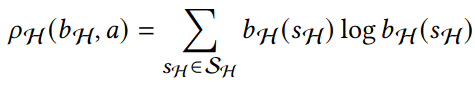
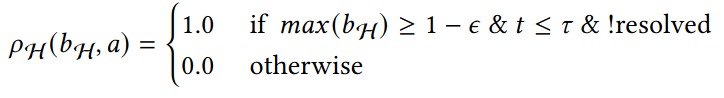
1. Minimize Entropy
2. Minimize Time to Decision
Two choices for info-gathering reward
Tree Search
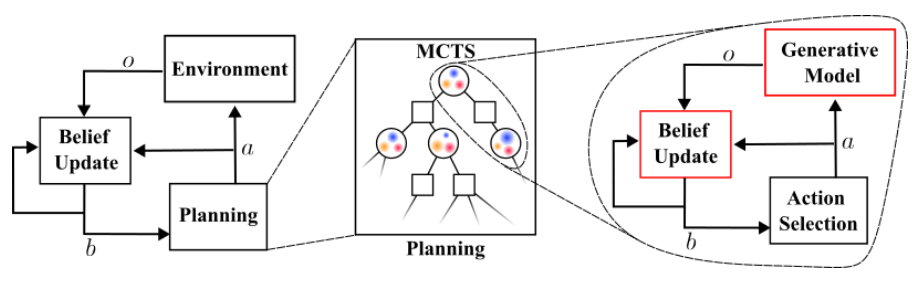
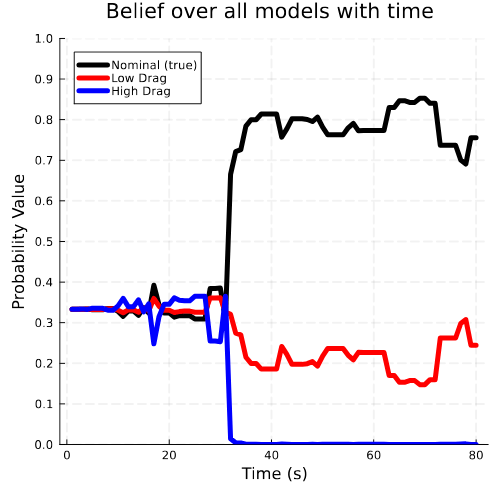
Results

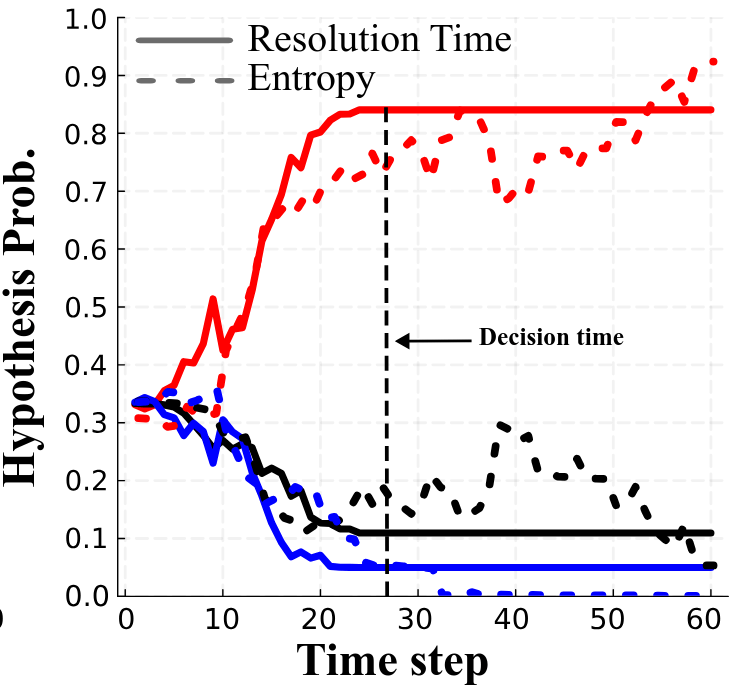
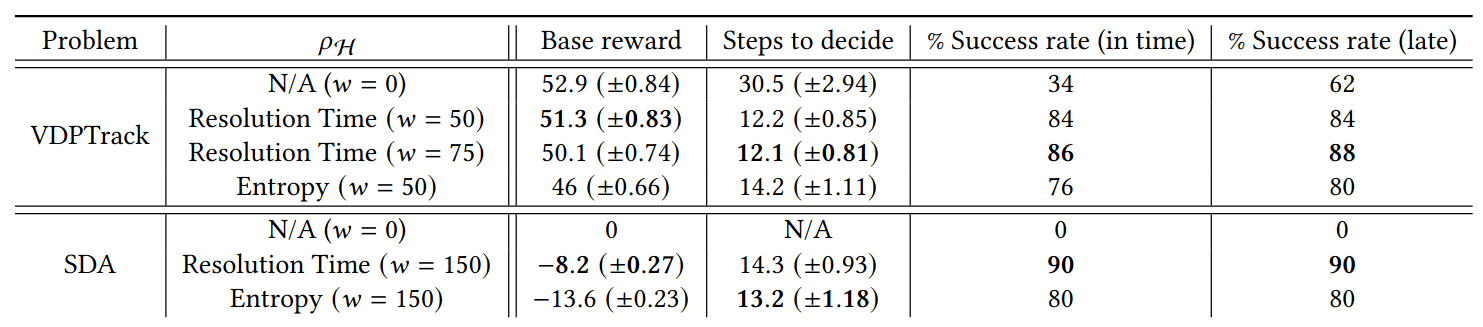
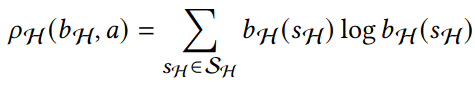
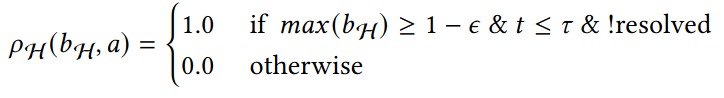
Resolution Time
Entropy
[Dagan, Becker & Sunberg, AAMAS '25 (under review)]
3. LLM-based hypothesis translation
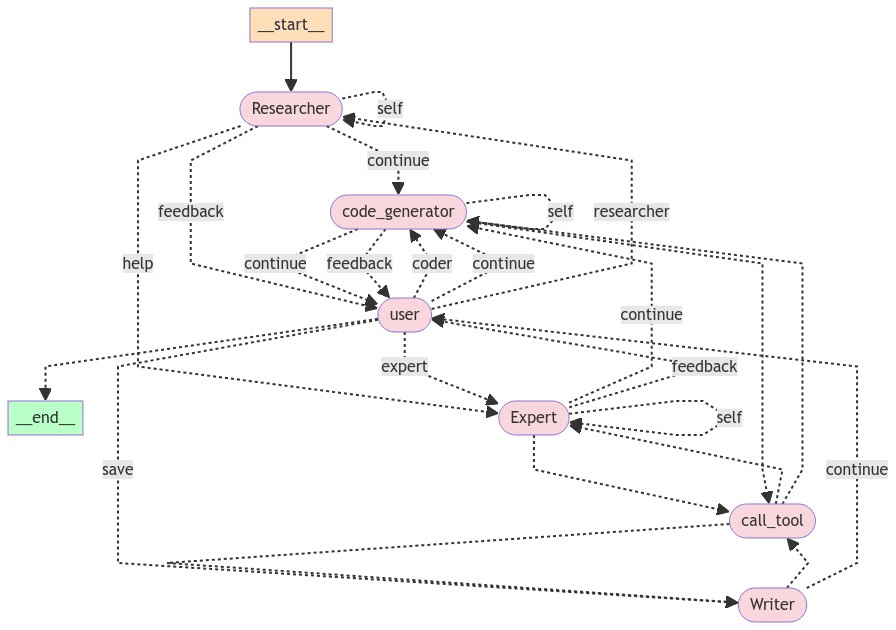
LLM-based hypothesis translation:
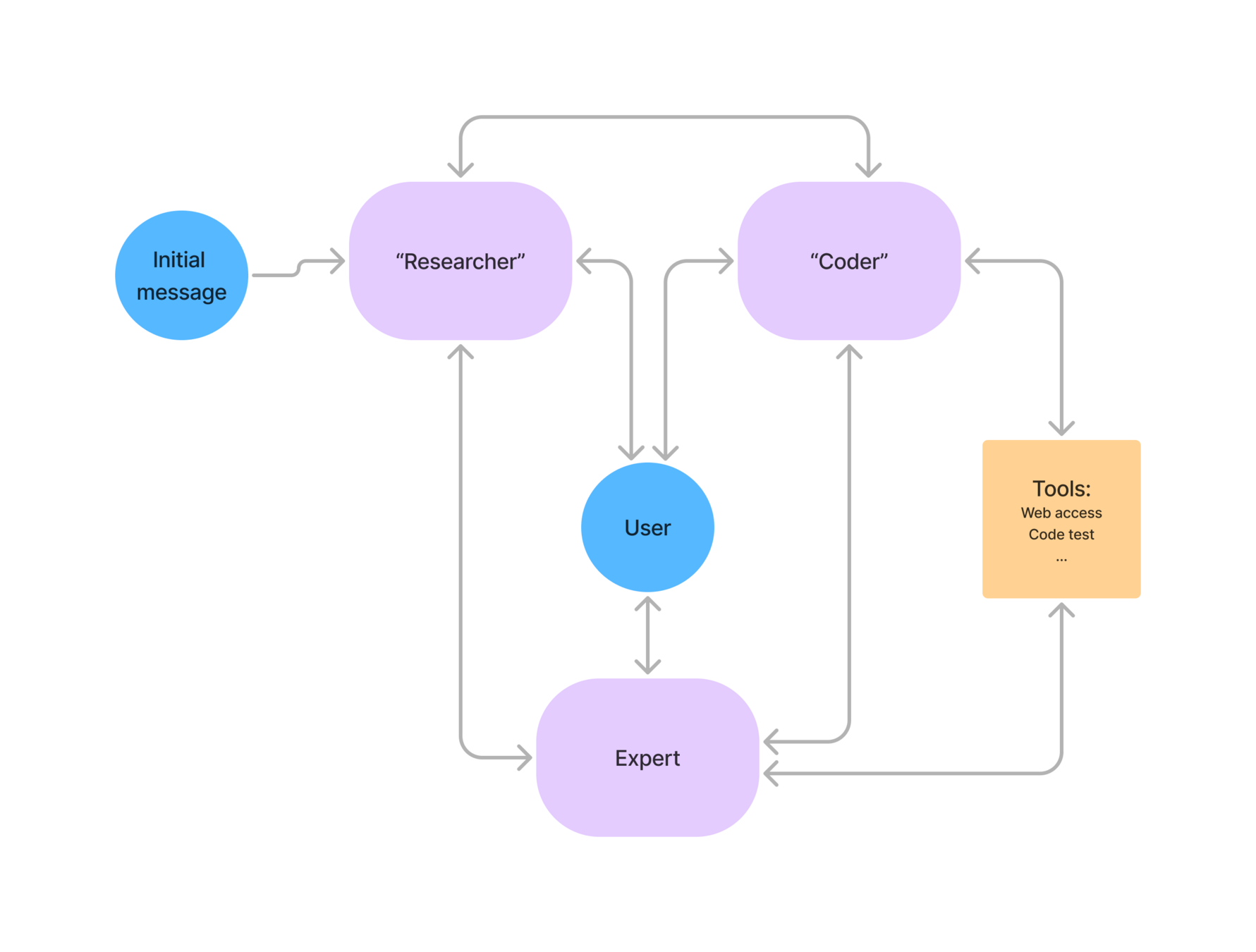
Natural Language Hypothesis
"The satellite deployed a 1m\(^2\) solar panel"
Code that simulates all effects of panel
(drag, change in natural frequency, etc.)
Prompt:
Agent descriptor
RESEARCH_AGENT_DESCRIPTION =
"""You are a helpful AI assistant, collaborating with other assistants.\n
The task at hand is {task}\n
Use the provided tools to progress towards fulfilling the task\n
If you are unable to fully answer, that's OK, another assistant with different tools \n
will help where you left off. Make as much progress as you can, but DO NOT WRITE CODE!\n
When you receive code from a code generating agent, examine it carefully to check if
it answers the full task instruction,
if it doesn't, reflect on the the missing parts and return it to the code_generator agent.
If you or any of the other assistant have the final answer or deliverable,
prefix your response with REQUEST FEEDBACK so the team knows wait to user input.\n
You have access to the following tools: {tool_names}.
before calling a tool ask yourself if you know the answer to what you are looking for,
if the answer is yes, don't call the tool. \n{system_message}"""- General problem prompt: describes the problem, gives examples
- Agent descriptor
- Agent specific directions
- Initial message
Prompt:
General prompt:
- General problem prompt: describes the problem, gives examples
- Agent descriptor
- Agent specific directions
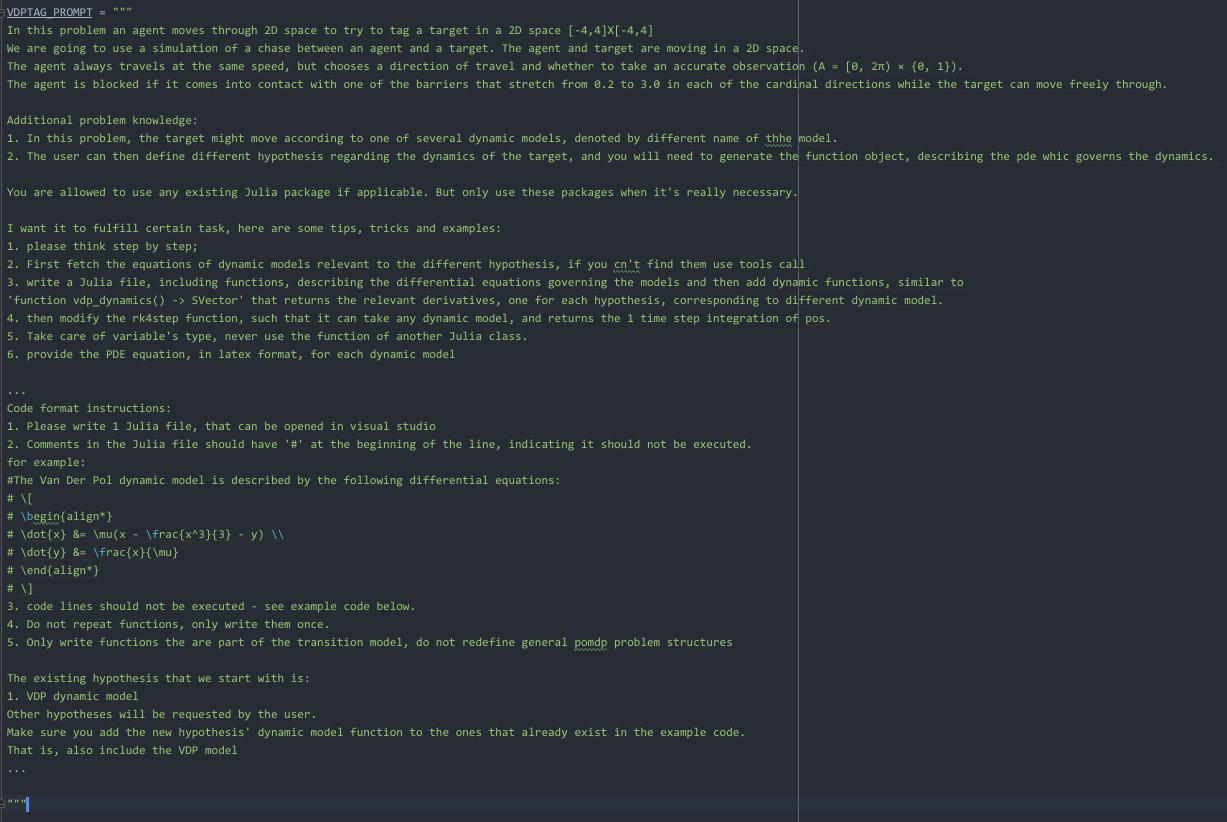
Add a Dubins car model to the code given in the prompt.
The model needs to be simple, with only x,y derivatives.
Once you code it up, finish.Example:


Example:

Example:
Followed by the code


Example:

Example:
# The Dubins car dynamic model in x-y plane is described
# by the following differential equations:
# \[
# \begin{align*}
# \dot{x} &= v \cdot \cos(\theta)
# \\
# \dot{y} &= v \cdot \sin(\theta)
# \end{align*}
# \]
module gptMultiDynamicsFunction
using ..MDHPOMDP
using StaticArrays
export dubins_car_dynamics
struct dubins_car_dynamics <: Function
v::Float64
theta::Float64
end
function (dyn::dubins_car_dynamics)(pos::Vec2)
x = pos[1]
y = pos[2]
return SVector(dyn.v*cos(dyn.theta), dyn.v*sin(dyn.theta))
end
end # module gptMultiDynamicsFunction4. Partially Observable Stochastic Games
Partially Observable Stochastic Games in Space


- Traditional dynamic game theory assumes full state observability
- POSGs allow modelling games of information
What if an adversary is actively trying to deceive you?
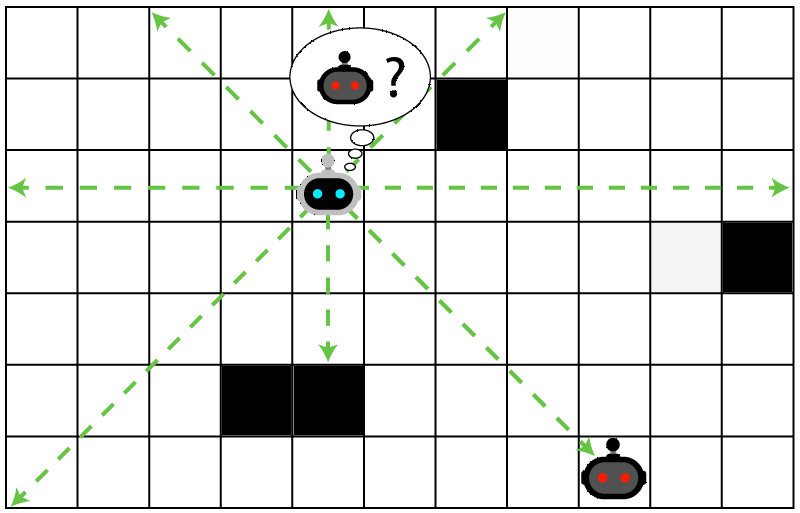
Laser Tag POMDP
Evader strategy:
Move away from pursuer
Embedded in \(T(s' \mid s, a)\)
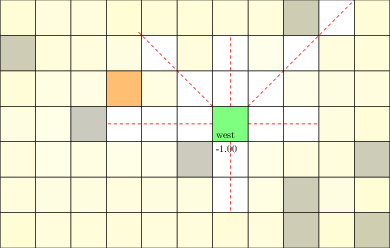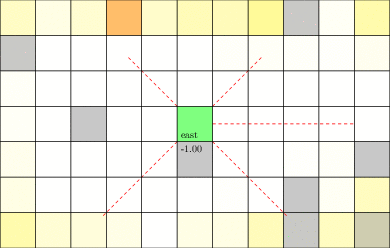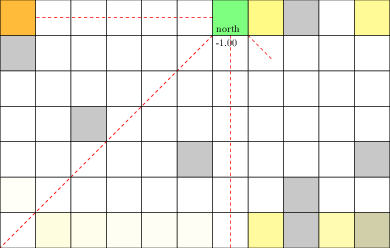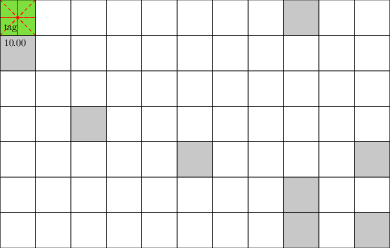
Laser Tag POMDP
Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward
- \(\mathcal{O}\) - Observation space
- \(\mathcal{Z}(o \mid s, a, s')\) - Observation probability distribution
Partially Observable Stochastic Game (POSG)
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, \bm{a})\) - Transition probability distribution
- \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
- \(R^i(s, \bm{a})\) - Reward function (cooperative, opposing, or somewhere in between)
- \(\mathcal{O}^i, \, i \in 1..k\) - Observation spaces
- \(Z(o^i \mid \bm{a}, s')\) - Observation probability distributions

Belief-based approach?


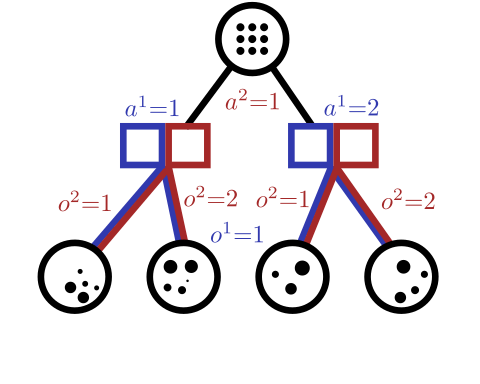
Finding a Nash Equilibrium: Poker
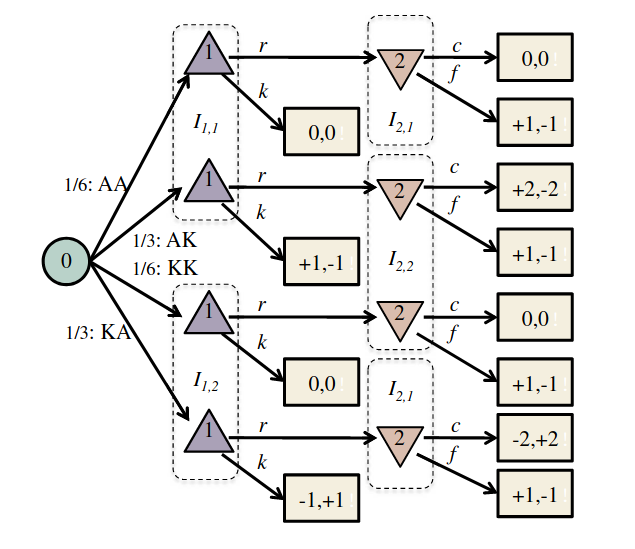
Image: Russel & Norvig, AI, a modern approach
P1: A
P1: K

P2: A
P2: A
P2: K
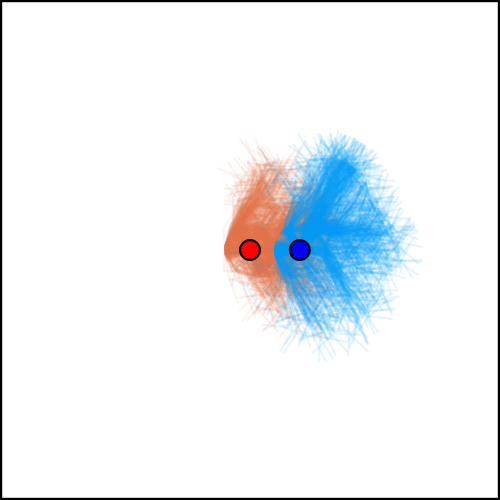
Conditional Distribution Info-set Tree (CDIT)
Regret Matching
(External Sampling Counterfactual Regret Minimization)
[Becker & Sunberg, AAMAS '25 (under review)]


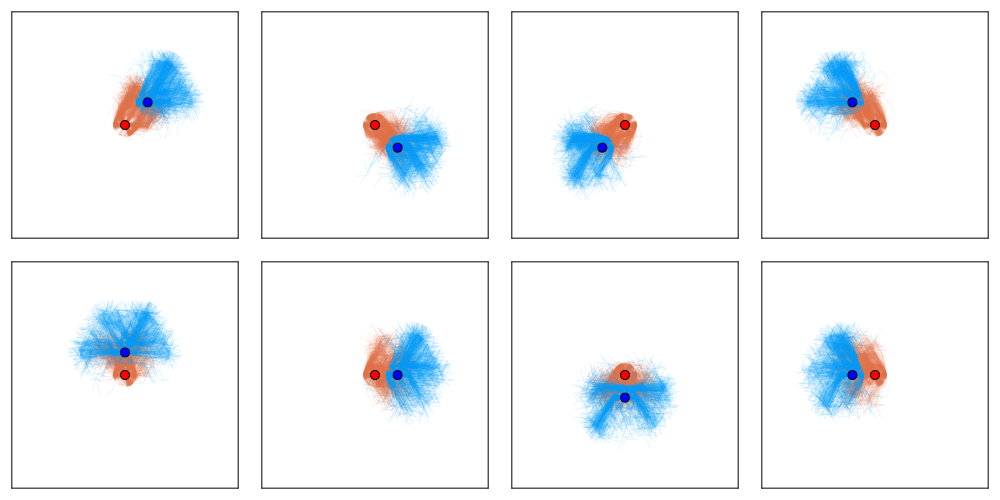
[Becker & Sunberg, AAMAS '25 (under review)]
Conditional Distribution Info-set Tree (CDIT)
Convergence Analysis for Games

Incentive to deviate:
Approximate Solutions

| -1, -1 | -10, 0 | |
| 0, -10 | -5, -5 |
\(\sigma^1_1\)
\(\sigma^1_2\)
\(\ldots\)
\(\sigma^2_1\)
\(\sigma^2_2\)
\(\vdots\)
| -1.01, -1.20 | -9.82, 0.12 | |
| -0.10, -10.5 | -4.89, -5.02 |
\(\sigma^1_1\)
\(\sigma^1_2\)
\(\ldots\)
\(\sigma^2_1\)
\(\sigma^2_2\)
\(\vdots\)
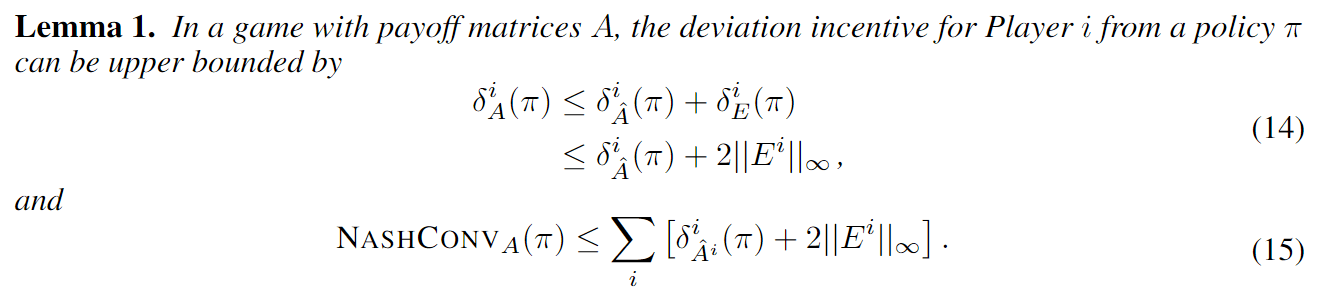
Incentive to deviate in approximate game \(\hat{A}\)
Maximum value approximation error (\(E^i = A^i - \hat{A}^i \))
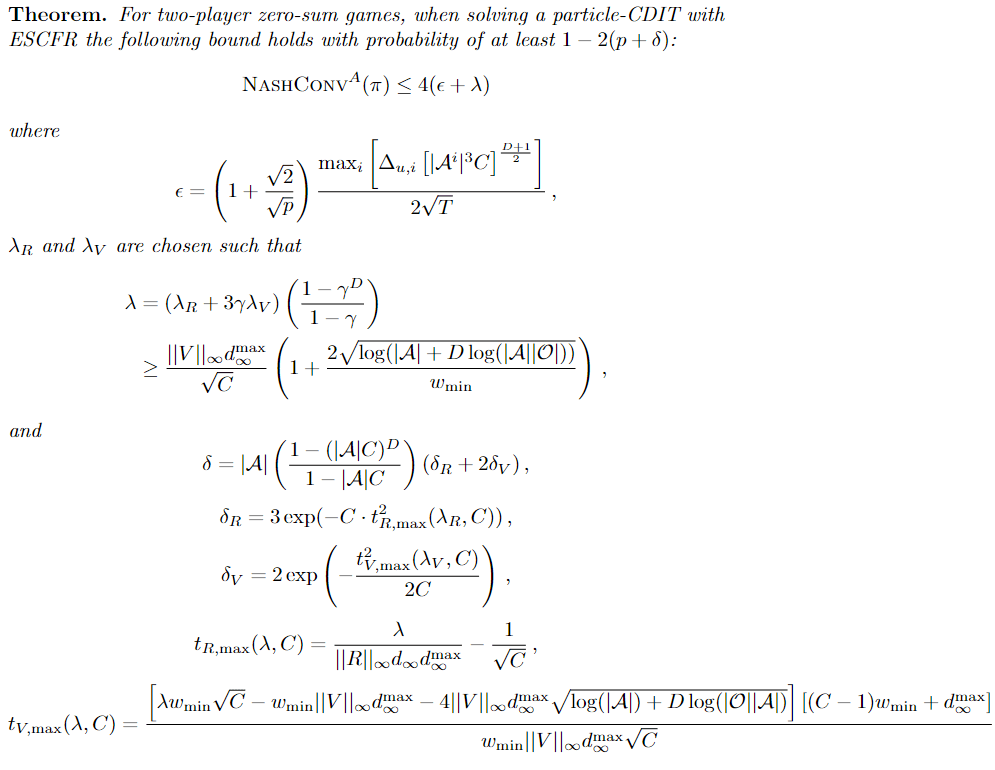
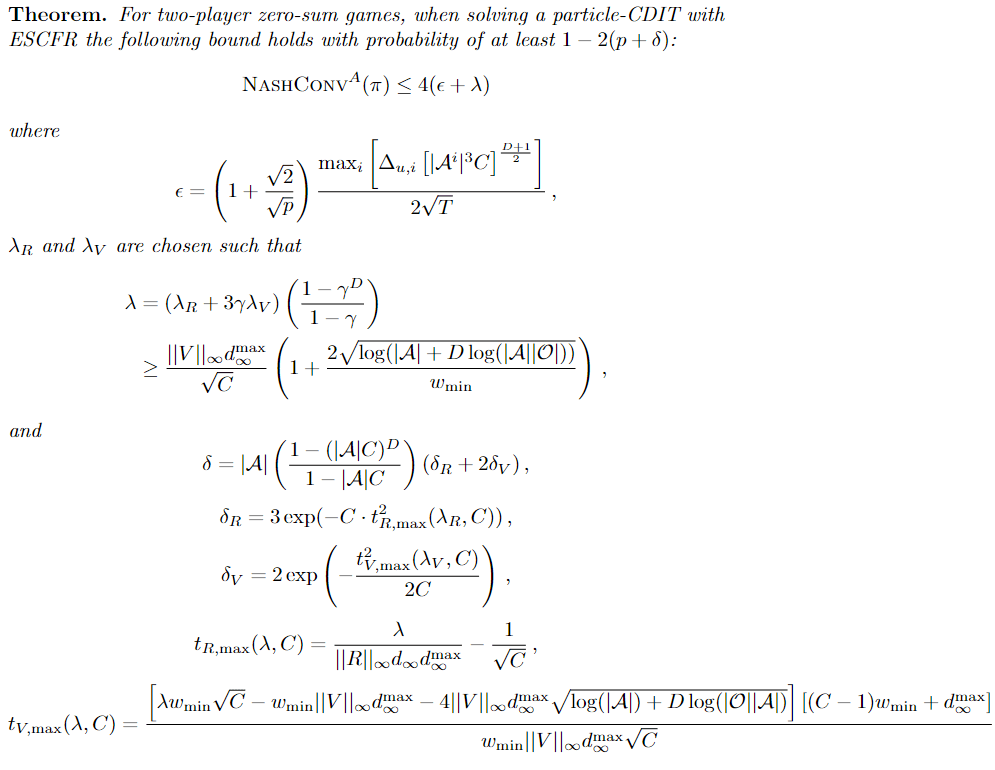
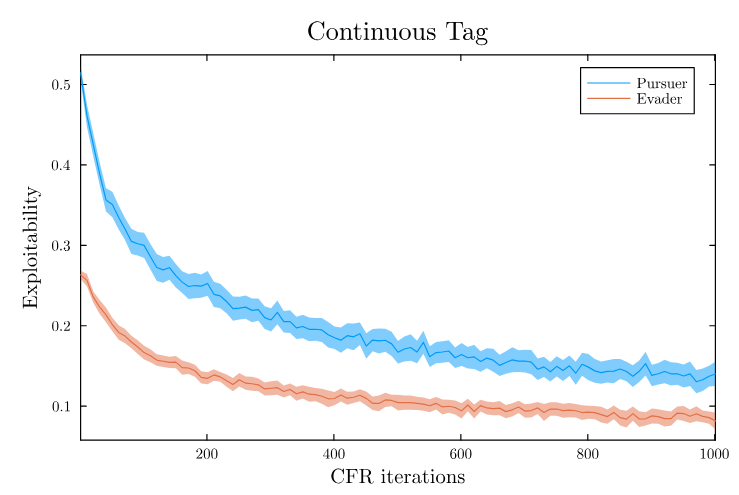
4. Future Plans
4. Future Plans
-
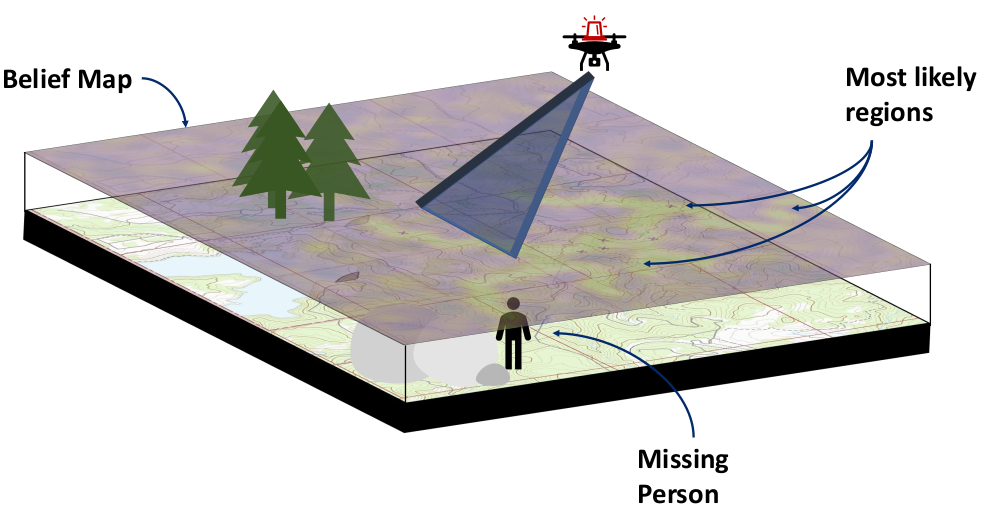
Integrate hypothesis-driven planning into user-facing software with Prof. Feigh's team at Georgia Tech
- Realistic data
- Question/hypothesis pipeline
- Focus on inference task before planning
-
Realistic Space Games
- Still limited to small action spaces
- Main goal: evaluate decrease in exploitability with game theoretic methods
Challenges
- What are the realistic situations that these decision-making aides could help in?
- What are the current operational priorities and difficulties for space force and are our hammers actually applicable to these nails? (JCO has been useful, but does not seem to encompass all of what the space force could be interested in - in particular, sensor tasking is different than what we are doing)
Thank You!



Dr. Ofer Dagan
Postdoctoral Associate
Tyler Becker
Doctoral Student
Regret Matching
Average regret bounds deviation incentive
Nash Equilibrium
Incentive to deviate makes a policy suboptimal
For a single agent:
For multiple agents:
Outline
- MDPs and POMDPs
- Solving POMDPs with tree search
- Breaking the curse of dimensionality
- Partially observable stochastic games
1. MDPs and POMDPs
Types of Uncertainty
Aleatory
Epistemic (Static)
Epistemic (Dynamic)


Interaction

MDP

RL
POMDP
Game
Example 2: Tornados
Video: Eric Frew
Example 2: Tornados
Video: Eric Frew
Example 2: Tornados
Video: Eric Frew
Markov Decision Process (MDP)

Aleatory

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)
\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)
\[\underset{\pi:\, \mathcal{S} \to \mathcal{A}}{\text{maximize}} \quad \text{E}\left[ \sum_{t=0}^\infty R(s_t, a_t) \right]\]
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward

State
Timestep
POMDP Example: Light-Dark
2. Solving POMDPs with Tree Search
Solving a POMDP
Environment
Belief Updater


True State
\(s = 7\)
Observation \(o = -0.21\)
\(b\)
\[b_t(s) = P\left(s_t = s \mid b_0, a_0, o_1 \ldots a_{t-1}, o_{t}\right)\]

\[ = P\left(s_t = s \mid b_{t-1}, a_{t-1}, o_{t}\right)\]
\(a\)
\[b_{t+1}(s') \propto Z(o \mid a, s')\int_{s \in \mathcal{S}} T(s' \mid s, a) b_t(s) ds\]
\(O(|\mathcal{S}|^2)\) for finite \(\mathcal{S}\)

State
Timestep
POMDP Example: Light-Dark
Solving a POMDP
Environment
Belief Updater
Planner
\(a = +10\)


True State
\(s = 7\)
Observation \(o = -0.21\)

\(b\)
\[b_t(s) = P\left(s_t = s \mid b_0, a_0, o_1 \ldots a_{t-1}, o_{t}\right)\]

\[ = P\left(s_t = s \mid b_{t-1}, a_{t-1}, o_{t}\right)\]
\(Q(b, a)\)
Why are POMDPs difficult?
- Curse of History
- Curse of dimensionality
- State space
- Observation space
- Action space
Tree size: \(O\left(\left(|A||O|\right)^D\right)\)

Curse of Dimensionality
\(d\) dimensions, \(k\) segments \(\,\rightarrow \, |S| = k^d\)



1 dimension
e.g. \(s = x \in S = \{1,2,3,4,5\}\)
\(|S| = 5\)
2 dimensions
e.g. \(s = (x,y) \in S = \{1,2,3,4,5\}^2\)
\(|S| = 25\)
3 dimensions
e.g. \(s = (x,y,x_h) \in S = \{1,2,3,4,5\}^3\)
\(|S| = 125\)
(Discretize each dimension into 5 segments)

\(x\)
\(y\)
\(x_h\)

3. Breaking the Curse of Dimensionality
Integration

Find \(\underset{s\sim b}{E}[f(s)]\)
\[=\sum_{s \in S} f(s) b(s)\]
Monte Carlo Integration
\(Q_N \equiv \frac{1}{N} \sum_{i=1}^N f(s_i)\)
\(s_i \sim b\) i.i.d.
\(\text{Var}(Q_N) = \text{Var}\left(\frac{1}{N} \sum_{i=1}^N f(s_i)\right)\)
\(= \frac{1}{N^2} \sum_{i=1}^N\text{Var}\left(f(s_i)\right)\)
\(= \frac{1}{N} \text{Var}\left(f(s_i)\right)\)
\[P(|Q_N - E[f(s_i)]| \geq \epsilon) \leq \frac{\text{Var}(f(s_i))}{N \epsilon^2}\]
(Bienayme)
(Chebyshev)
Curse of dimensionality!
Particle Filter POMDP Approximation
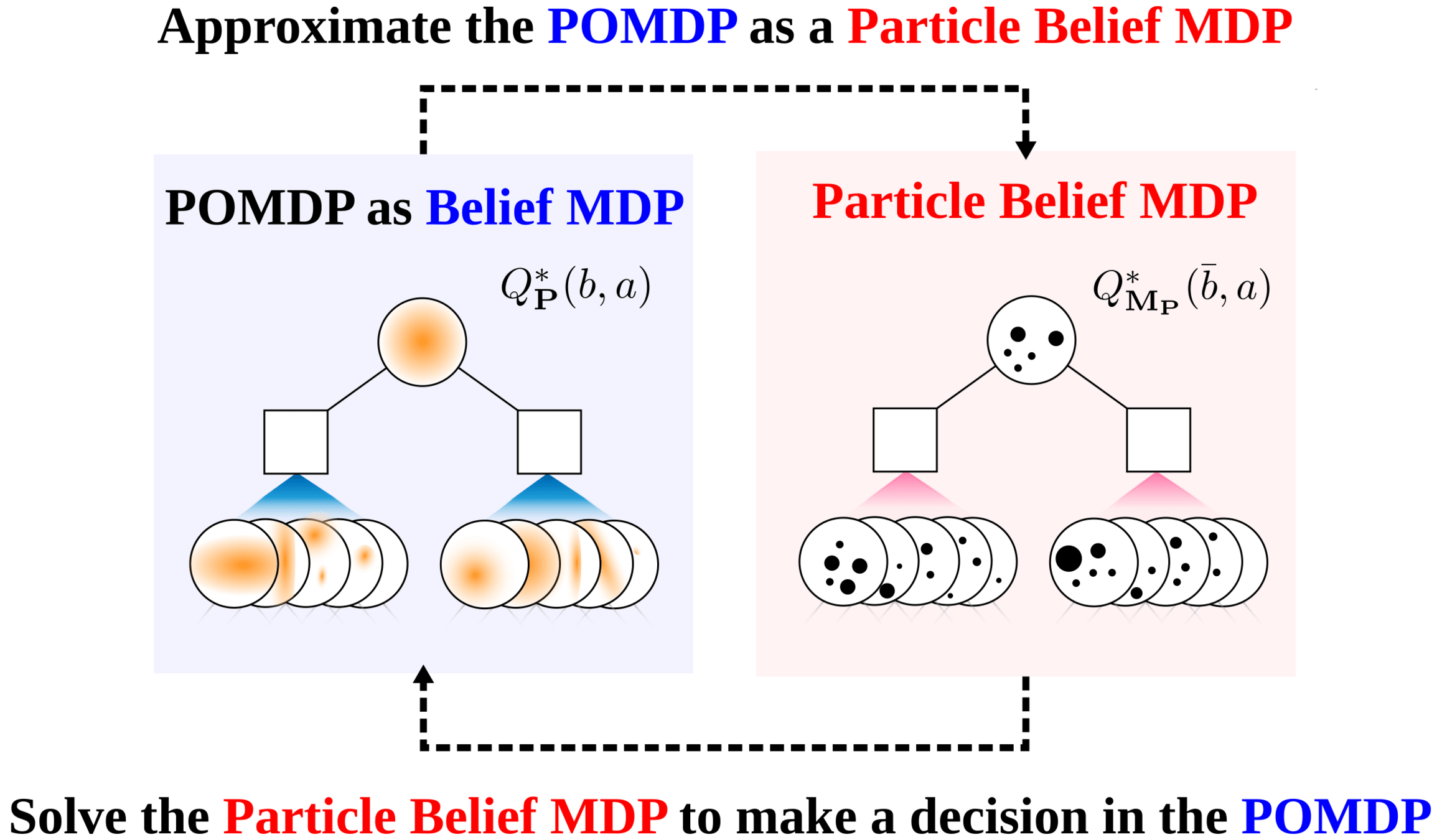
\[b(s) \approx \sum_{i=1}^N \delta_{s}(s_i)\; w_i\]
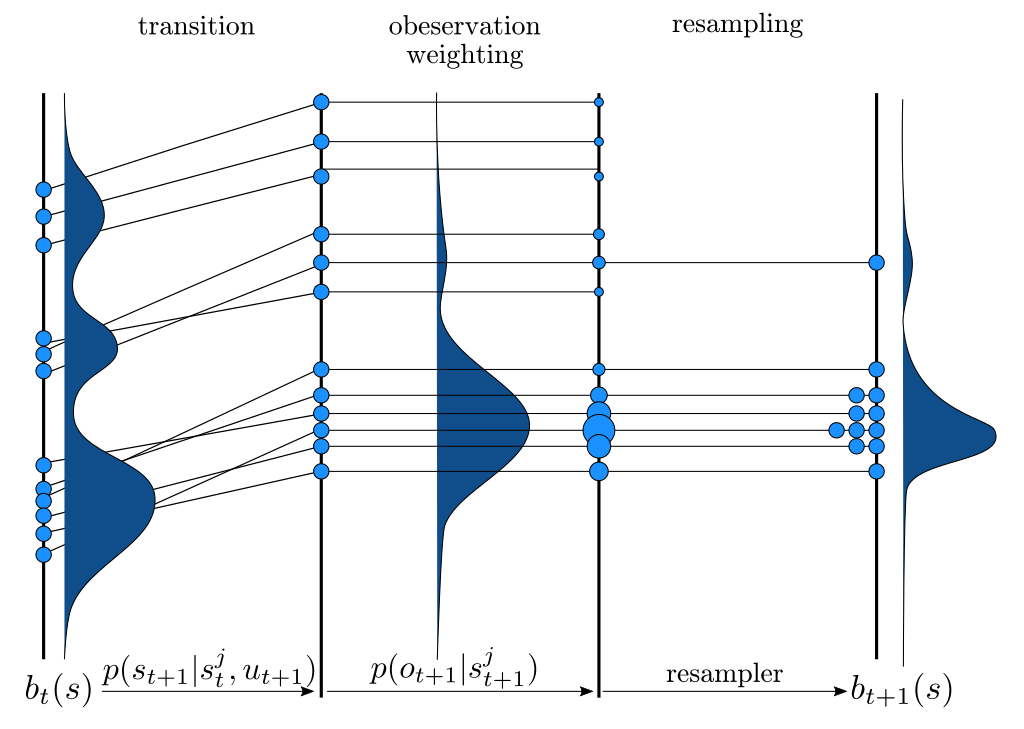
\[b_{t+1}(s') \propto Z(o \mid a, s')\int_{s \in \mathcal{S}} T(s' \mid s, a) b_t(s)\]
\(\implies\) Sample \(s'_i\) from \(T(s' | s_i, a)\),
\(w'_i \propto w_i \times Z(o \mid a, s'_i)\)

Example: Autonomous Driving
POMDP Formulation
\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)
\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)
\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

Ego external state
External states of other cars
Internal states of other cars
External states of other cars

- Actions shielded (based only on external states) so they can never cause crashes
- Braking action always available
Efficiency
Safety

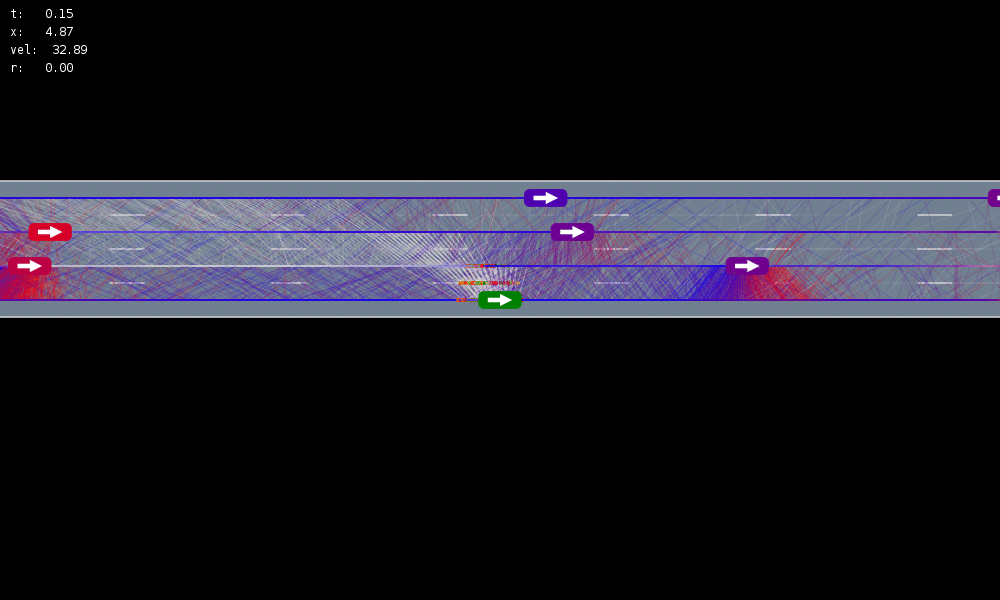






MDP trained on normal drivers



MDP trained on all drivers
Omniscient
POMCPOW (Ours)
Simulation results
[Sunberg & Kochenderfer, T-ITS 2023]
Convergence?
Key 1: Self Normalized Infinite Renyi Divergence Concentation
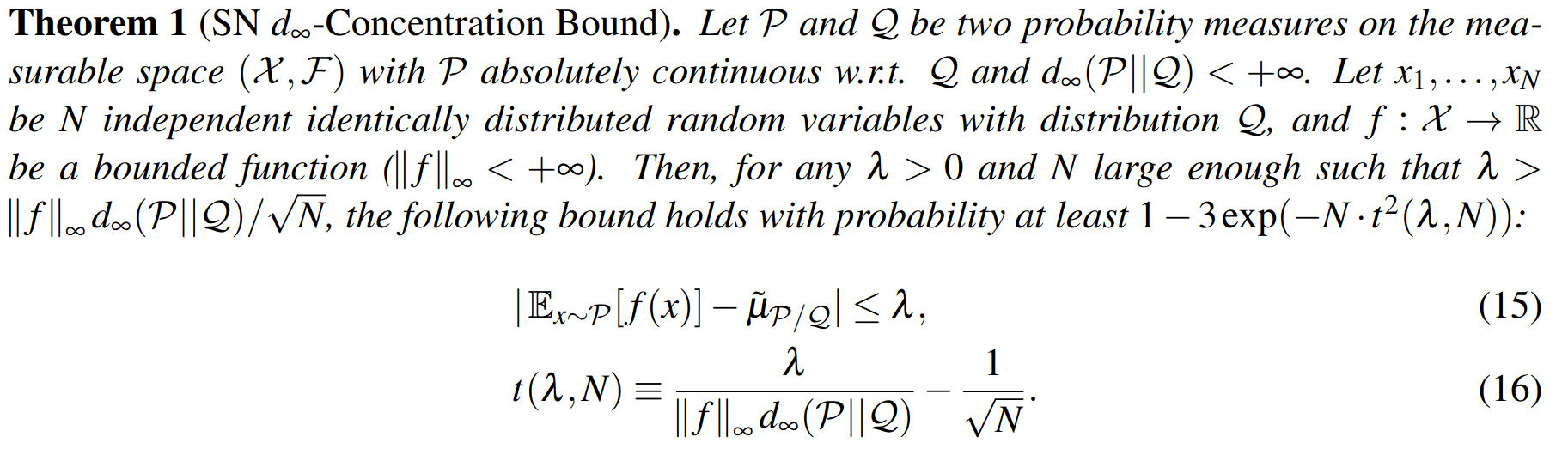
\(\mathcal{P}\): state distribution conditioned on observations (belief)
\(\mathcal{Q}\): marginal state distribution (proposal)
Key 2: Sparse Sampling
Expand for all actions (\(\left|\mathcal{A}\right| = 2\) in this case)
...
Expand for all \(\left|\mathcal{S}\right|\) states
\(C=3\) states

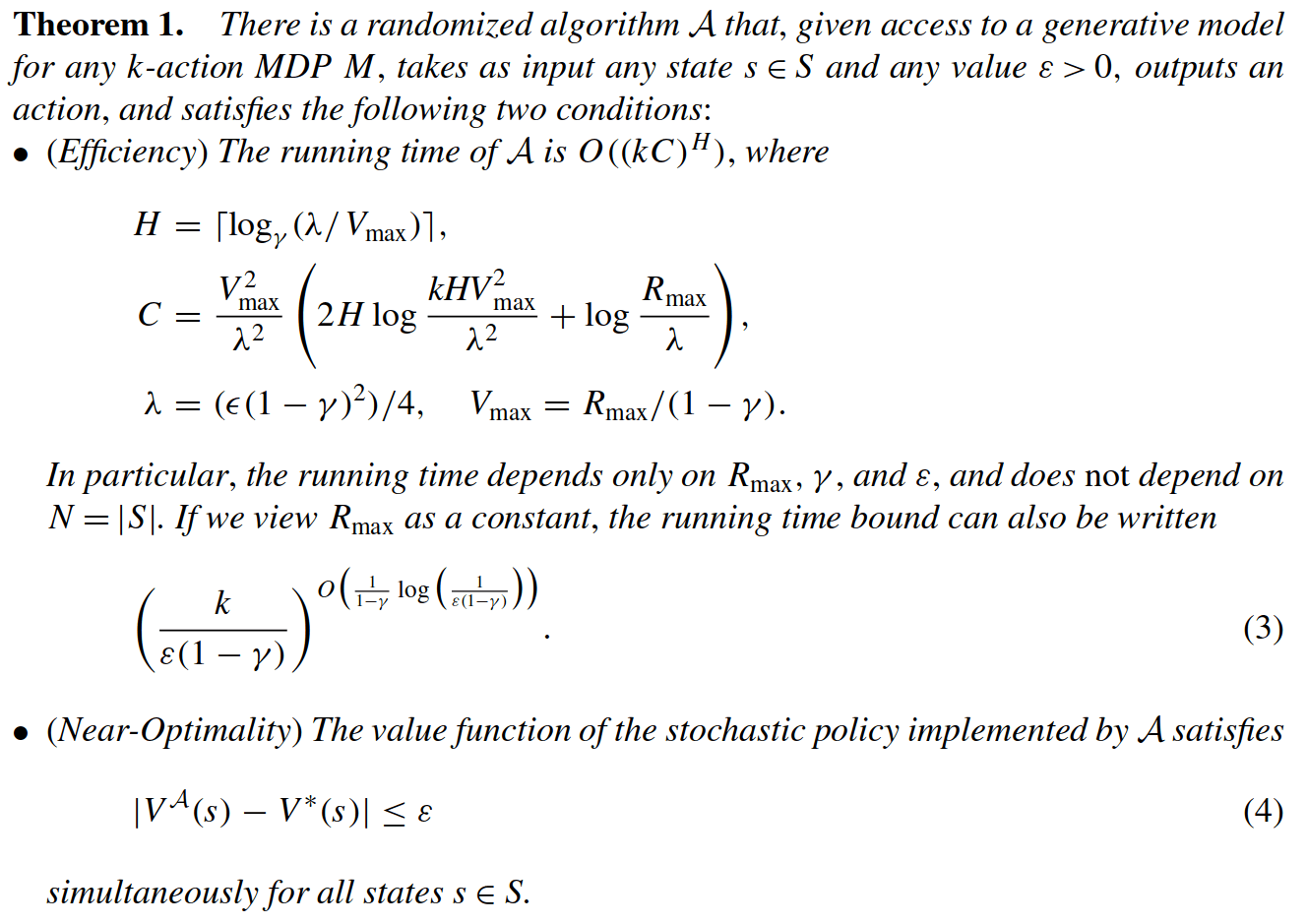
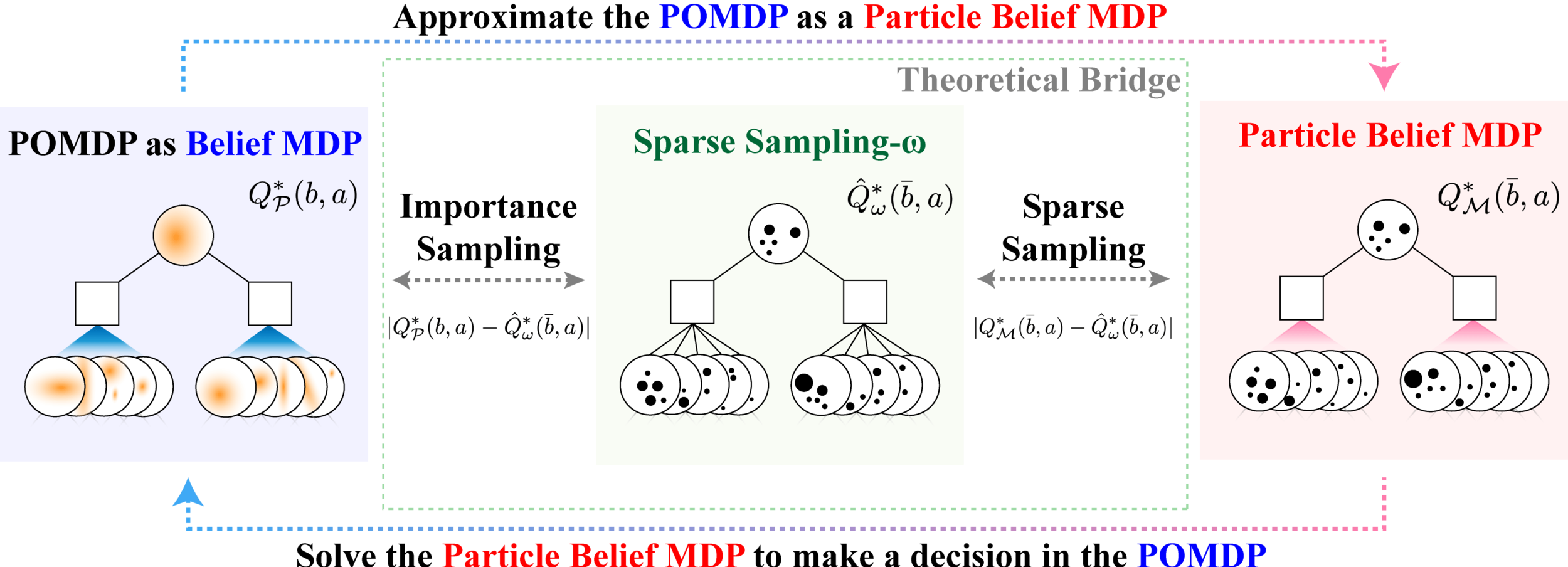
SS-\(\omega\) is close to Belief MDP

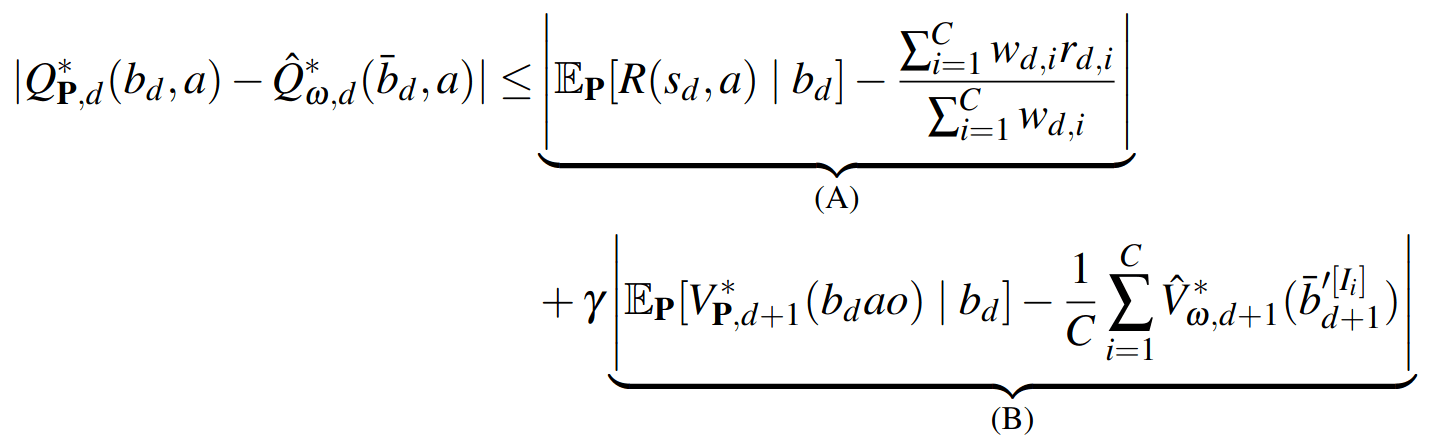
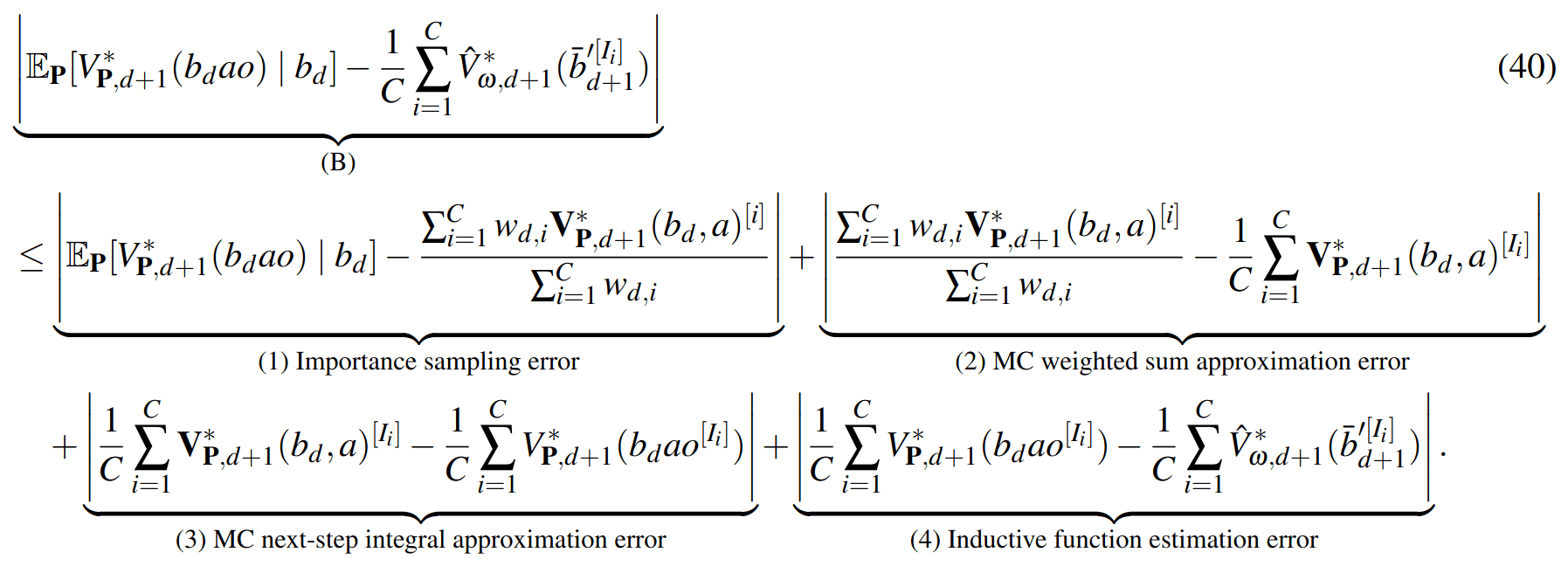
SS-\(\omega\) close to Particle Belief MDP (in terms of Q)

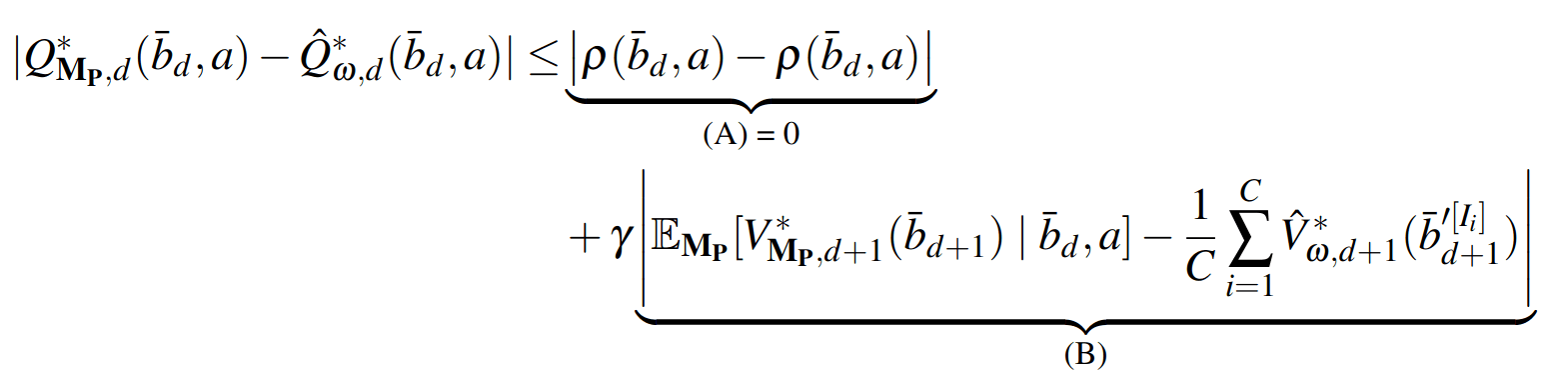
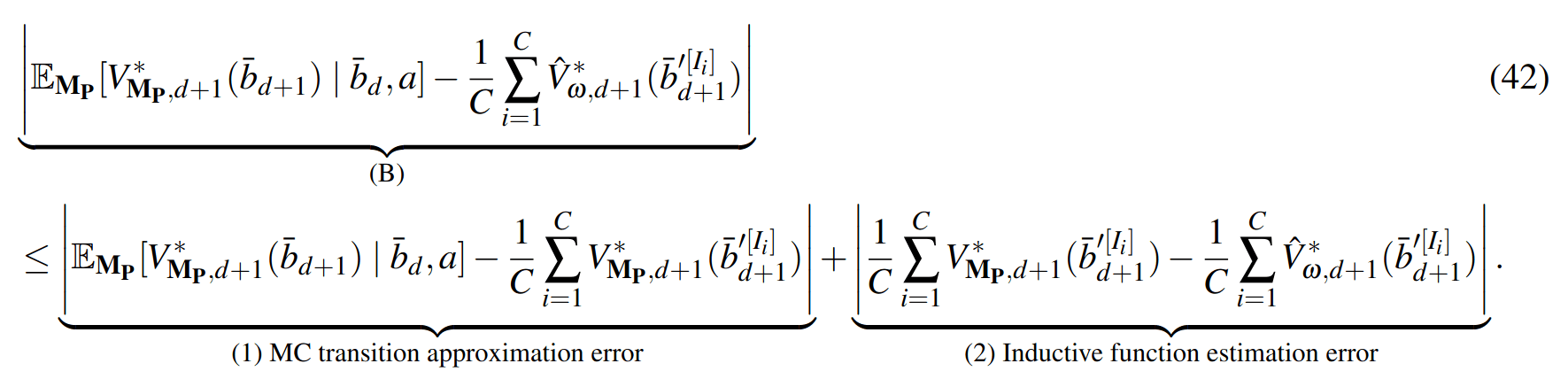
PF Approximation Accuracy
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]
For any \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,
[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]
No direct dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!

Particle belief planning suboptimality

\(C\) is too large for any direct safety guarantees. But, in practice, works extremely well for improving efficiency.
[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]

Why are POMDPs difficult?
- Curse of History
- Curse of dimensionality
- State space
- Observation space
- Action space

Tree size: \(O\left(\left(|A|C\right)^D\right)\)
Solve simplified surrogate problem for policy deep in the tree

[Lim, Tomlin, and Sunberg, 2021]
Takeaways
- POMDPs:
- If you have enough knowledge (e.g. sampleable T and explicit Z), solve as a particle belief MDP
- Don't worry too much about the curse of dimensionality in the state or observation space (Sparse sampling + particle filtering will help it)
- POSGs:
- Belief-based approaches are a losing battle
- One approach is CDIT - unifies particle-filtering POMDP methods


4. Partially observable stochastic games (POSGs)
POMDP Planning with Learned Components
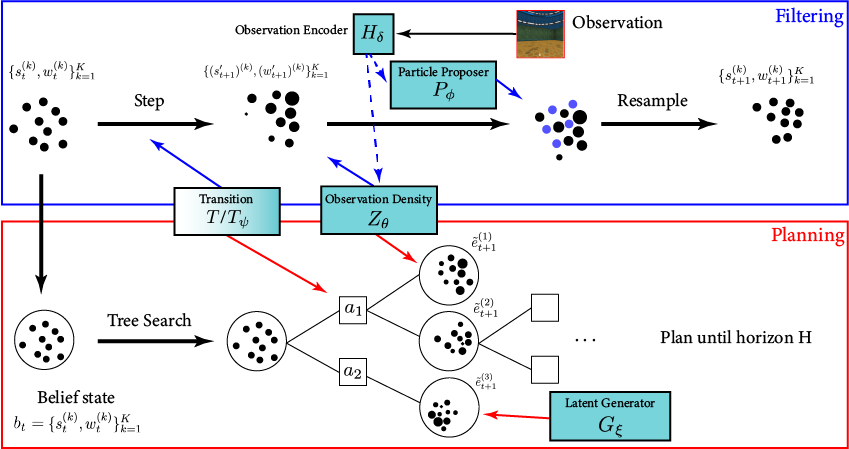
[Deglurkar, Lim, Sunberg, & Tomlin, 2023]
SURI IRT 3 Sunberg Year 1
By Zachary Sunberg
SURI IRT 3 Sunberg Year 1
- 409



