Dynamic Games
- Markov Games
- 2 Player zero sum turn taking games
Markov Games
Markov Game Definition
Markov Game Definition
\[(I, S, A, T, R, \gamma)\]
- \(I\) = set of players
- \(S\) = state space (combined for all players)
- \(A\) = joint action space
- \(T\) = transition distributions: \(T(s' \mid s, a)\) is the distribution of \(s'\) given state \(s\) and joint action \(a\)
- \(R\) = joint reward function: \(R^i(s, a)\) is the reward for agent \(i\) in state \(s\) when joint action \(a\) is taken
Goofspiel (or Game of Pure Strategy)
Goofspiel(5) Optimal Strategy
Calculated with Dynamic Programming [Rhoads and Bartholdi, 2012]
This is not a game payoff matrix!
Nash equilibrium at every state
Reduction to Simple Game
Reduction to Simple Game
Best response in a Markov Game
Best response in a Markov Game
Fictitious Play in a Markov Game
Fictitious Play in a Markov Game
Loop:
1. Simulate with \(\pi^{BR}\)
2. Update \(N(j, a^j, s)\) (\(N\) should reflect *all* past simulations)
2. \(\pi^j (a^j \mid s) \propto N(j, a^j, s) \quad \forall j\)
3. \(\pi^{BR} \gets\) best response to \(\pi\)
\(\pi\) (not necessarily \(\pi^{BR}\)) converges to a Nash equilibrium in some cases, notably 2-player zero-sum games
Markov Game Recap
- Definition \((I, S, A, T, R, \gamma)\)
- Reduction to simple game
- Computing a best response means solving an MDP - know how to construct the MDP
Turn-taking Games
Terminology
- Max and Min players
- deterministic
- two player
- zero-sum
- perfect information
Minimax Trees
Minimax Tree
MDP Expectimax Tree
\[V(s) = \text{max}_{a \in \mathcal{A}}\left(R(s, a) + \text{E}[V(s')]\right)\]
\[V(s) = \text{max}_{a \in \mathcal{A_1}}\left(R(s, a) + \text{min}_{a' \in A_2} (R(s', a') + V(s''))\right)\]
Tic-Tac-Toe Example
Tree Backup Example
Why is this harder than an MDP? (think back to sparse sampling)
Alpha-Beta Pruning
MCTS for Games
Note: the above example does not follow UCB exploration
Imperfect Information
Partially Observable Markov Game
Belief updates?
Reduction to Simple Game
Reduction to Simple Game
Extensive Form Game
(Alternative to POMGs that is more common in the literature)
- Similar to a minimax tree for a turn-taking game
- Chance nodes
- Information sets
Extensive Form Game
(Alternative to POMGs that is more common in the literature)
- Similar to a minimax tree for a turn-taking game
- Chance nodes
- Information sets
Extensive Form Game
Extensive-form game definition (\(h\) is a sequence of actions called a "history"):
- Finite set of \(n\) players, plus the "chance" player
- \(P(h)\) (player at each history)
- \(A(h)\) (set of actions at each history)
- \(I(h)\) (information set that each history maps to)
- \(U(h)\) (payoff for each leaf node in the game tree)
King-Ace Poker Example
- 4 Cards: 2 Aces, 2 Kings
- Each player is dealt a card
- P1 can either raise (\(r\)) the payoff to 2 points or check (\(k\)) the payoff at 1 point
- If P1 raises, P2 can either call (\(c\)) Player 1's bet, or fold (\(f\)) the payoff back to 1 point
- The highest card wins
King-Ace Poker Example
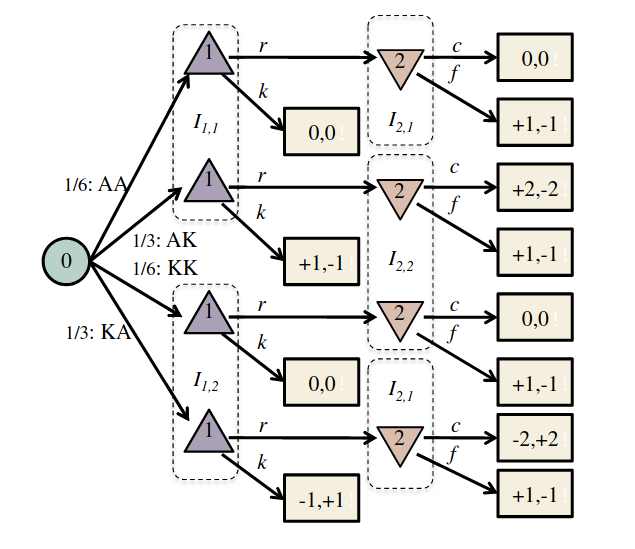
- 4 Cards: 2 Aces, 2 Kings
- Each player is dealt a card
- P1 can either raise (\(r\)) the payoff to 2 points or check (\(k\)) the payoff at 1 point
- If P1 raises, P2 can either call (\(c\)) Player 1's bet, or fold (\(f\)) the payoff back to 1 point
- The highest card wins
Extensive to Matrix Form
Exponential in number of info states!
Fictitious Play in Extensive Form Games
This slide not covered on exam
Heinrich et al. 2015 "Fictitious Self Play in Extensive-Form Games"
250 Dynamic Games
By Zachary Sunberg
