Bayesian Network Learning
-
Last time:
- Conditional independence in Bayesian Networks
- Sampling from Bayesian Networks
-
Today:
- Given a Bayesian Network and some values, how do we calculate the probability of other values?
- Given data, how do we fit a Bayesian network?
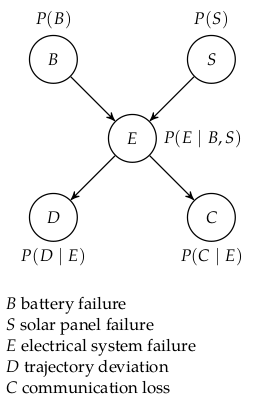
Bayesian Network
Structure
Parameters
Inference
Inputs
- Bayesian network structure
- Bayesian network parameters
- Values of evidence variables
Outputs
- Posterior distribution of query variables

Given that you have detected a trajectory deviation, and the battery has not failed what is the probability of a solar panel failure?
\(P(S=1 \mid D=1, B=0)\)
Exact
Approximate
Exact Inference
Exact Inference

\[P(S{=}1 \mid D{=}1, B{=}0)\]
\[= \frac{P(S{=}1, D{=}1, B{=}0)}{P(D{=}1, B{=}0)}\]
\[P(S{=}1, D{=}1, B{=}0) = \sum_{e, c}P(B{=}0, S{=}1, E{=}e, D{=}1, C{=}c)\]
\[P(B{=}0, S{=}1, E, D{=}1, C)\]
\[= P(B{=}0)\,P(S{=}1)\,P(E\mid B{=}0, S{=}1)\,P(D{=}1\mid E)\,P(C{=}1\mid E)\]
\(2^5= 32\) possible assignments, but quickly gets too large
Exact Inference

\(2^5= 32\) possible assignments, but quickly gets too large
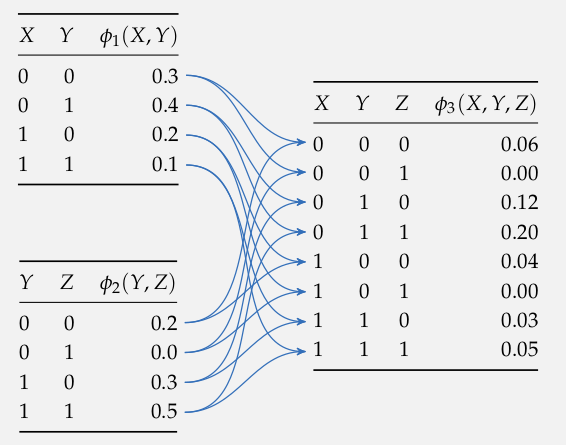
Product
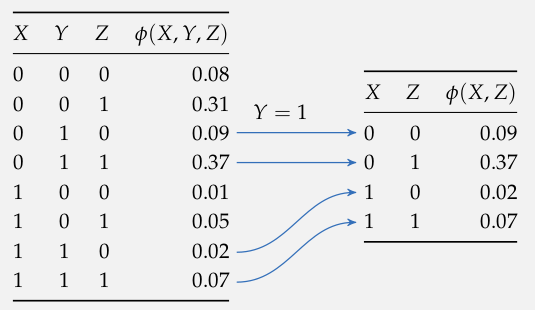
Condition
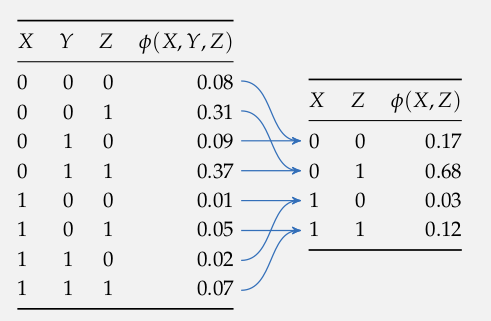
Marginalize

Exact Inference: Variable Elimination

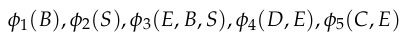
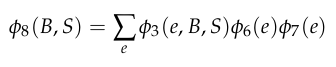
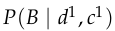
Start with
Eliminate \(D\) and \(C\) (evidence) to get \(\phi_6(E)\) and \(\phi_7(E)\)
Eliminate \(E\)
Eliminate \(S\)
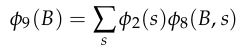
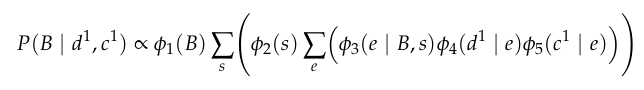
vs
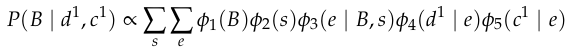
Choosing optimal order is NP-hard
Approximate Inference

Approximate Inference: Direct Sampling
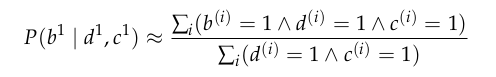

Analogous to
unweighted particle filtering

Approximate Inference: Weighted Sampling
Analogous to
weighted particle filtering
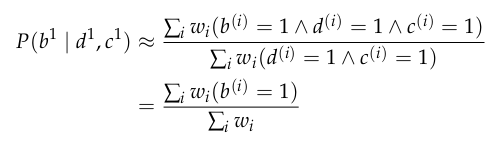


Approximate Inference: Gibbs Sampling
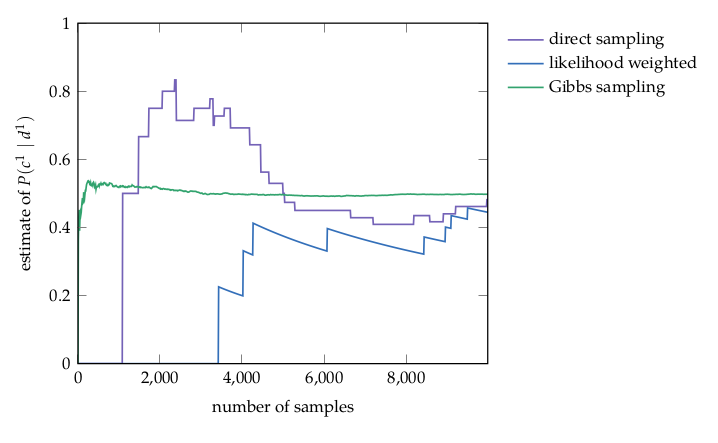
Markov Chain Monte Carlo (MCMC)
Learning
Bayesian Network Learning
Inputs
- Data, \(D\)
- Priors (?)
Outputs
- Bayesian network structure, \(G\)
- Bayesian network parameters, \(\theta\)
Counting Parameters
For discrete R.V.s:
\[\text{dim}(\theta_X) = \left(|\text{support}(X)|-1\right)\prod_{Y \in Pa(X)} |\text{support}(Y)|\]

Structure Learning Example
Parameter Learning
Maximum Likelihood
Bayesian




Multinomial:


Multinomial:

Structure Learning






NP-Hard
Markov Equivalence Class

Markov Equivalent iff
- Same undirected edges
- Same set of immoral v-structures

Recap
Inference
Learning
230 Bayesian Network Learning
By Zachary Sunberg
230 Bayesian Network Learning
- 935



