POMDP Formulation Approximations
Recap
- Alpha Vectors
- Best solver for discrete POMDPs:
POMDP Computational Complexity
- Infinite horizon POMDPs are undecidable
- Finite horizon POMDPs are PSPACE Complete
- Among the hardest problems that can be solved using a polynomial amount of space
- Any algorithm that can solve a general POMDP will have exponential complexity
(we think)
Sad facts ðŸ˜
Approximate POMDP Solutions
Numerical Approximations
(approximately solve original problem)
Offline
Online
Formulation Approximations
(solve a slightly different problem)
Last week
Thursday
Today!
Rotor Failure Example
POMDP Objective
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
Certainty Equivalent
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
\[\pi_{\text{CE}}(b)Â = \pi_s (\underset{s\sim b}{\text{E}[s])}\]
\[b' = \tau(b, a, o)\]
Certainty Equivalent
Optimal for LQG
QMDP
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
\[\pi_\text{QMDP}(b)Â = \underset{a \in A}{\text{argmax}} \,\, \underset{s\sim b}{\text{E}}\left[Q_\text{MDP}(s, a)\right]\]
\[b' = \tau(b, a, o)\]
Example: Tiger POMDP with Waiting
\begin{aligned}
& \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\
& s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\
& \mathcal{A} = \{-10, -1, 0, 1, 10\} \\
& R(s, a) = \begin{cases}
100 & \text{ if } a = 0, s = 0 \\
-100 & \text{ if } a = 0, s \neq 0 \\
-1 & \text{ otherwise}
\end{cases} & \\
\end{aligned}
State
Timestep
Accurate Observations
Goal: \(a=0\) at \(s=0\)
Optimal Policy
Localize
\(a=0\)
POMDP Example: Light-Dark
POMDP Solution
QMDP
Same as full observability on the next step
Information Gathering
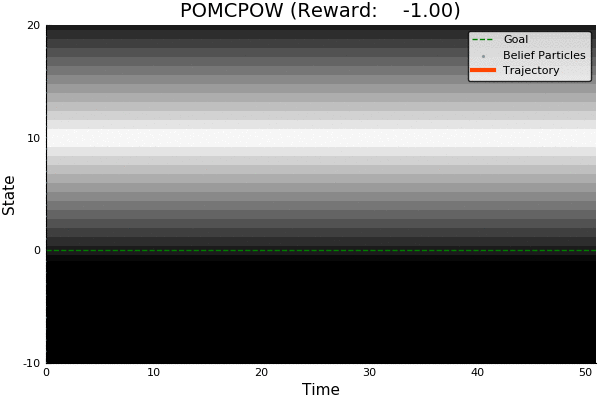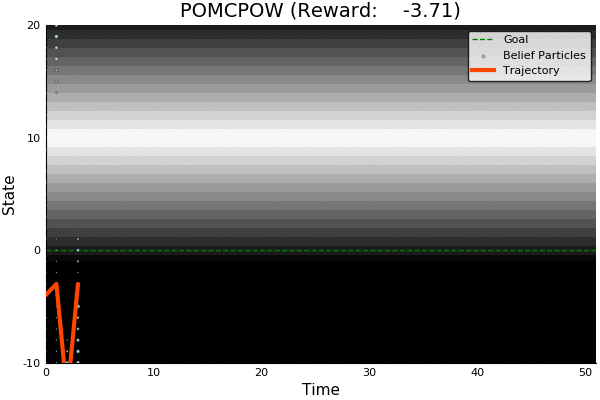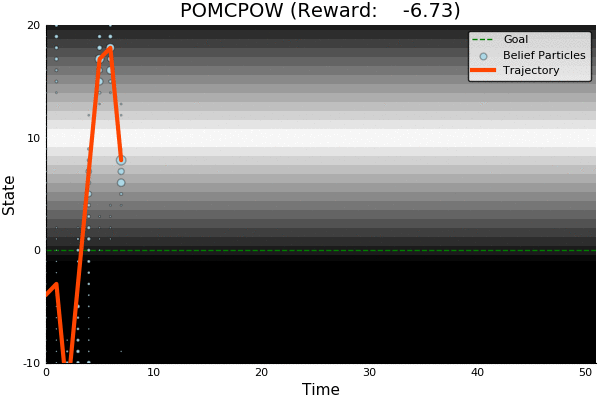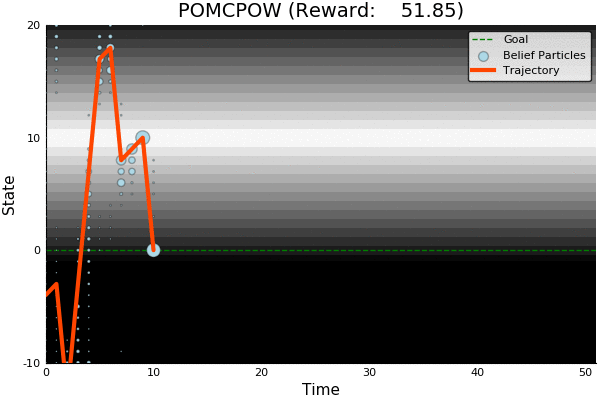
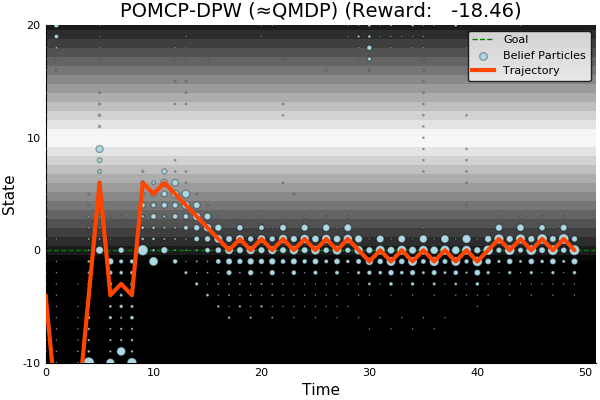
QMDP
Full POMDP
QMDP
INDUSTRIAL GRADE
QMDP
ACAS X
[Kochenderfer, 2011]
Hindsight Optimization
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
FIB
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
k-Markov
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
Open Loop
\[\pi^*Â = \underset{\pi : B \to A}{\text{argmax}} \,\, \text{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t, \pi(b_t))\right]\]
\[b' = \tau(b, a, o)\]
POMDP Objective
190 POMDP Formulation Approximations
By Zachary Sunberg
