Bayesian Networks:
Inference and Independence
For next year: revise to causal BNs
Bayesian Networks
Today:
- Bayesian Networks
- How do we perform inference on Bayesian Networks?
- How do we reason about independence in Bayesian Networks?
Review
Review
Independence
\(P(X, Y) = P(X)\, P(Y)\)
Conditional Independence
\(P(X, Y \mid Z) = P(X \mid Z) \, P(Y \mid Z)\)
2022 Quiz 1
Joint Distribution Complexity
Binary Random Variables \(X_1\), \(X_2\), \(X_3\)
How many independent parameters (\(\theta\)) to specify joint distribution?
7
For \(n\) binary R.V.s, \(2^n-1\) independent parameters specify the joint distribution.
In general \[\dim(\theta) = \prod_{i=1}^n |\text{support}(X_i)| - 1\]
Bayesian Network
Bayesian Network: Directed Acyclic Graph (DAG) that represents a joint probability distribution
- Node:
- Edges encode:
Random Variable
\[P(X_{1:n}) = \prod_{i=1}^n P(X_i \mid \text{pa}(X_i))\]
Full Story: "
Counting Parameters
For discrete R.V.s:
\[\text{dim}(\theta_X) = \left(|\text{support}(X)|-1\right)\prod_{Y \in Pa(X)} |\text{support}(Y)|\]
Inference
Inputs
- Bayesian network structure
- Bayesian network parameters
- Values of evidence variables
Outputs
- Posterior distribution of query variables
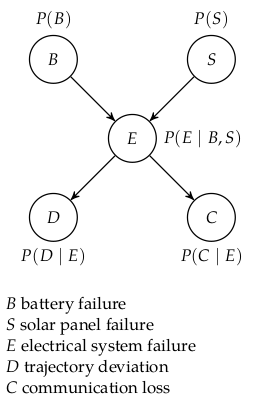
Given that you have detected a trajectory deviation, and the battery has not failed what is the probability of a solar panel failure?
\(P(S=1 \mid D=1, B=0)\)
Exact
Approximate
Exact Inference
Exact Inference
\[P(S{=}1 \mid D{=}1, B{=}0)\]
\[= \frac{P(S{=}1, D{=}1, B{=}0)}{P(D{=}1, B{=}0)}\]
\[P(S{=}1, D{=}1, B{=}0) = \sum_{e, c}P(B{=}0, S{=}1, E{=}e, D{=}1, C{=}c)\]
\[P(B{=}0, S{=}1, E, D{=}1, C)\]
\[= P(B{=}0)\,P(S{=}1)\,P(E\mid B{=}0, S{=}1)\,P(D{=}1\mid E)\,P(C{=}1\mid E)\]
Exact Inference
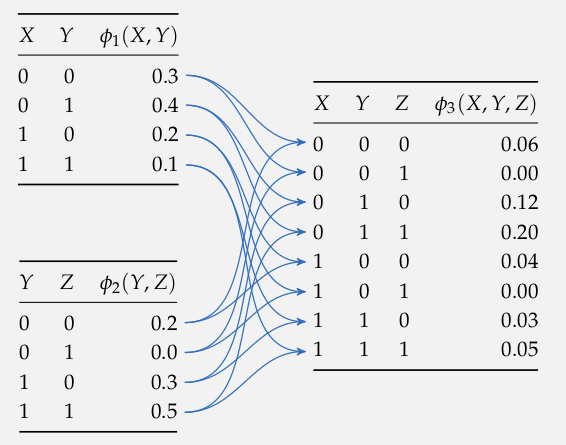
Product
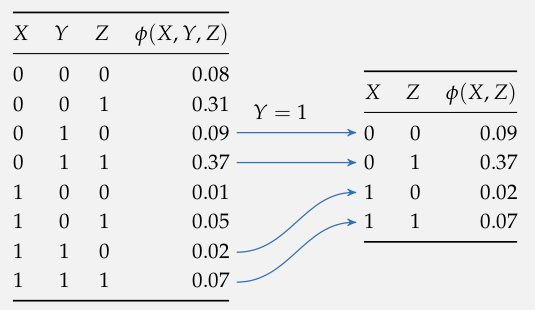
Condition
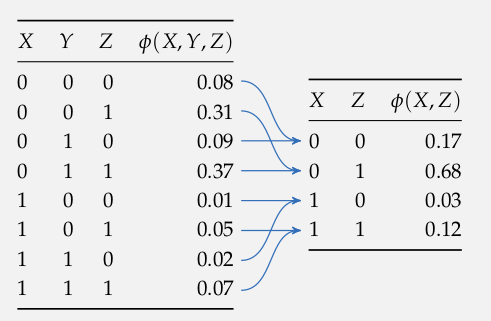
Marginalize
Exact Inference
Exact Inference: Variable Elimination
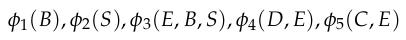
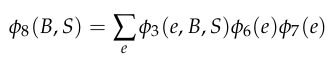
Start with
Eliminate \(D\) and \(C\) (evidence) to get \(\phi_6(E)\) and \(\phi_7(E)\)
Eliminate \(E\)
Eliminate \(S\)
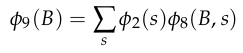
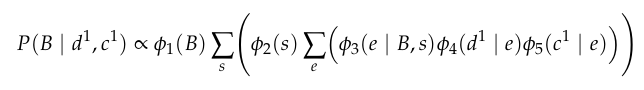
vs
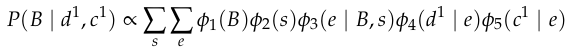
Choosing optimal order is NP-hard
Next Year: Skip
Approximate Inference
Approximate Inference: Direct Sampling
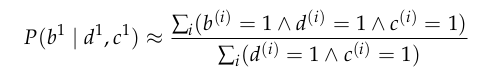
Analogous to
unweighted particle filtering
Approximate Inference: Weighted Sampling
Analogous to
weighted particle filtering
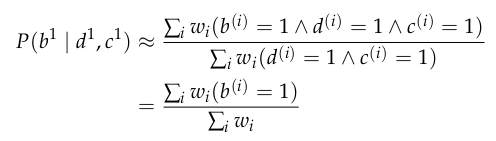
Approximate Inference: Gibbs Sampling
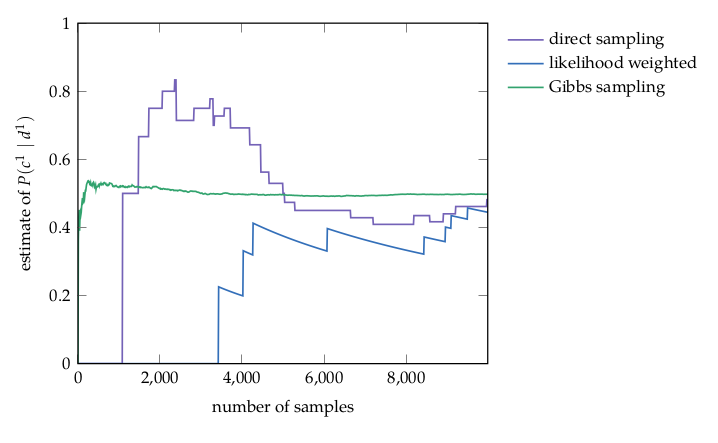
Markov Chain Monte Carlo (MCMC)
Break
What does conditional independence mean?
All of \(X\)'s influence on \(Y\) comes through \(Z\)
\(X \perp Y \mid Z\)
\(\implies\)
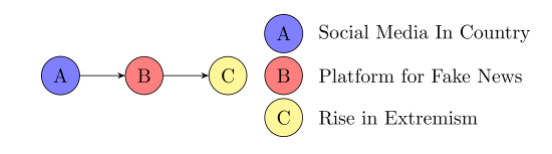
\(A \perp C \mid B\) ?
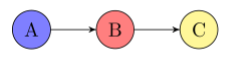
Mediator
Yes
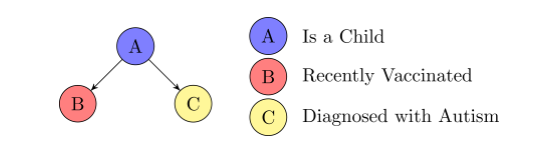
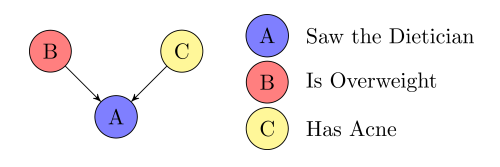
\(B \perp C \mid A\) ?
Confounder
Yes
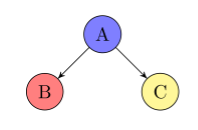
\(B \perp C \mid A\) ?
Collider
Inconclusive
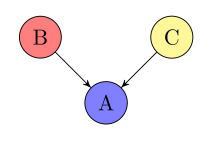
https://kunalmenda.com/2019/02/21/causation-and-correlation/
\(P(X \mid Z) = P(X \mid Y, Z)\)
More Complex Example
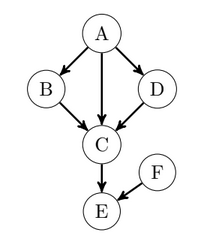
\((B\perp D \mid A)\) ?
\((B\perp D \mid E)\) ?
Yes!
Inconclusive
Why is this relevant to decision making?
d-Separation
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y\) is not in \(\mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
Let \(\mathcal{C}\) be a set of random variables.
A path between \(A\) and \(B\) is d-separated* by \(\mathcal{C}\) if any of the following are true
We say that \(A\) and \(B\) are d-separated by \(\mathcal{C}\) if all paths between \(A\) and \(B\) are d-separated by \(\mathcal{C}\).
If \(A\) and \(B\) are d-separated by \(\mathcal{C}\) then \(A \perp B \mid \mathcal{C}\)
*short for "directionally separated"
Proving Conditional Independence
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
- Enumerate all (non-cyclic) paths between nodes in question
- Check all paths for d-separation
- If all paths d-separated, then CE
Example: \((B \perp D \mid C, E)\) ?
Exercise
\(D \perp C \mid B\) ?
\(D \perp C \mid E\) ?
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
Sampling from a Bayesian Network
Given a Bayesian network, how do we sample from the joint distribution it defines?
- Topoligical Sort (If there is an edge \(A \rightarrow B\), then \(A\) comes before \(B\))
- Sample from conditional distributions in order of the topological sort
Analogous to Simulating a (PO)MDP
Recap
025 Bayesian Networks
By Zachary Sunberg
