Causal Bayesian Networks
Causal Bayesian Networks
Today:
- Causal Bayesian Networks
- How do we reason about independence in Bayesian Networks?
Review: Distributions of Discrete R.V.s
Joint
\(P(X=x, Y=y)\)
Shorthand: \(P(x, y)\)
\(P(X, Y)\)
Single number
"Probability that \(X=x\) and \(Y=y\)"
"Joint distribution of \(X\) and \(Y\)"
A table
Conditional
A collection of tables for each \(y\)
\(P(X=x\mid Y=y)\)
Shorthand: \(P(x \mid y)\)
\(P(X \mid Y)\)
Single number
"Probability that \(X=x\) if \(Y=y\)"
"Conditional distribution of \(X\) given \(Y\)"
Marginal
\(P(X=x)\)
Shorthand: \(P(x)\)
\(P(X)\)
Single number
A table
"Probability that \(X=x\)"
"Marginal distribution of \(X\)"
Causal Bayesian Networks
A Bayesian Network compactly represents a joint probability distributions using two components:
- Structure: a directed acyclic graph (DAG), where each node is a R.V.
- Parameters: Numerical values that determine a conditional distribution at each node
At each node, \(P(X \mid pa(X))\)
In a Causal Bayesian Network, arrows denote causation.
\(B\) is a result of \(A\) (and some aleatory uncertainty)
Chain rule for Bayesian Networks
\[P(X_{1:n}) = \prod_{i=1}^n P(X_i \mid \text{pa}(X_i))\]
Simple Causal Bayes Net Example
Naive Inference on Bayes Nets
Bayes Net with 3 Random Variables: \(A \rightarrow C \rightarrow B\)
Want to find \(P(\underbrace{A=a}_\text{query} \mid \underbrace{B=b}_\text{evidence})\)
- \(P(A, B=b, C) = P(B=b \mid C) \, P(C \mid A) \, P(A)\).
- Marginalize over hidden and query variables to get \[P(A=a, B=b) = \sum_c P(A=a, B=b, C=c)\] and
\[P(B=b) = \sum_{a, c} P(A=a, B=b, C=c)\] - \(P(A=a \mid B=b) = \frac{P(A=a, B=b)}{P(B=b)}\)
\(C\) is a "hidden variable"
(Book introduces unnormalized "factors", but process is the same.)
Conditional Independence in Bayes Nets
Conditional Independence: Fork
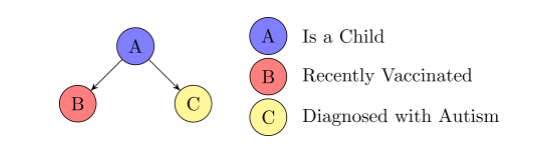
\(B \perp C \mid A\) ?
Yes
https://kunalmenda.com/2019/02/21/causation-and-correlation/
Conditional Independence: Inverted Fork
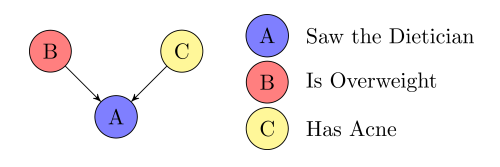
\(B \perp C \mid A\) ?
https://kunalmenda.com/2019/02/21/causation-and-correlation/
Next year, swap examples
More Complex Example
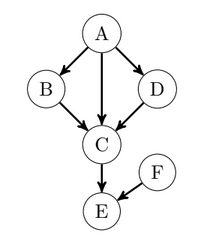
\((B\perp D \mid A)\) ?
\((B\perp D \mid E)\) ?
Yes!
Inconclusive
Why is this relevant to decision making?
d-Separation
Let \(\mathcal{C}\) be a set of random variables.
An undirected path between \(A\) and \(B\) is d-separated by \(\mathcal{C}\) if any of the following exist along the path:
Separators (a.k.a "inactive triples"):
- Chain: \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- Fork: \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- Inverted Fork (v-structure): \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
Also:
- d-separated = "inactive"
- not d-separated = "active"
\(B \leftarrow A \rightarrow C \leftarrow D\)
\(B \leftarrow C \rightarrow A \leftarrow D\)
Break
Are these paths d-separated by \(\mathcal{C} = \{C\}\)?
d-Separation for Bayes Nets
We say that \(A\) and \(B\) are d-separated by \(\mathcal{C}\) if all acyclic paths between \(A\) and \(B\) are d-separated by \(\mathcal{C}\).
If \(A\) and \(B\) are d-separated by \(\mathcal{C}\) then \(A \perp B \mid \mathcal{C}\)
*short for "directionally separated"
In other words, if there is any active path w.r.t. \(\mathcal{C}\) between \(A\) and \(B\), we cannot conclude that \(A \perp B \mid \mathcal{C}\) based on the structure alone.
Proving Conditional Independence
Separators
- Chain: \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- Fork: \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- Inverted Fork (v-structure): \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
- Enumerate all (non-cyclic) paths between nodes in question
- Check all paths for d-separation
- If all paths d-separated, then C.I.
Example: \((B \perp D \mid C, E)\) ?

Markov Blanket
The Markov Blanket of \(\mathcal{X}\) is the minimal set of nodes that, if their values were known, would make \(\mathcal{X}\) conditionally independent of all other nodes.
A Markov blanket of a particular node consists of its parents, its children, and the other parents of its children.
If \(\mathcal{B}\) is the Markov blanket of \(\mathcal{X}\), you can treat analyze \(\mathcal{B} \cup \mathcal{X}\) alone, and ignore any other nodes.
Exercise

\(D \perp C \mid B\) ?
\(D \perp C \mid E\) ?
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\) and no descendant of \(Y\) is in \(\mathcal{C}\).
Approximate Inference

Approximate Inference: Direct Sampling
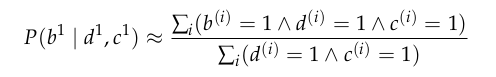

Analogous to
unweighted particle filtering

Approximate Inference: Weighted Sampling
Analogous to
weighted particle filtering
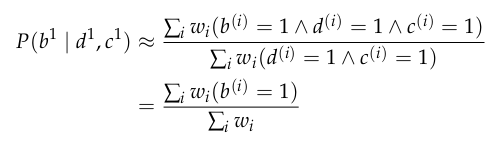


Approximate Inference: Gibbs Sampling
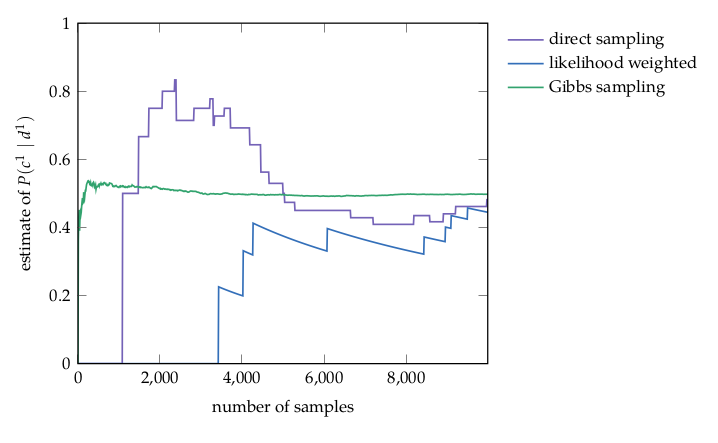
Markov Chain Monte Carlo (MCMC)
Sampling from a Bayesian Network
Given a Bayesian network, how do we sample from the joint distribution it defines?

- Topoligical Sort (If there is an edge \(A \rightarrow B\), then \(A\) comes before \(B\))
- Sample from conditional distributions in order of the topological sort
Analogous to Simulating a (PO)MDP
Recap
Review
Independence
\(P(X, Y) = P(X)\, P(Y)\)
Conditional Independence
\(P(X, Y \mid Z) = P(X \mid Z) \, P(Y \mid Z)\)
2022 Quiz 1

Joint Distribution Complexity
Binary Random Variables \(X_1\), \(X_2\), \(X_3\)
How many independent parameters (\(\theta\)) to specify joint distribution?
7
For \(n\) binary R.V.s, \(2^n-1\) independent parameters specify the joint distribution.
In general \[\dim(\theta) = \prod_{i=1}^n |\text{support}(X_i)| - 1\]
Bayesian Network
Bayesian Network: Directed Acyclic Graph (DAG) that represents a joint probability distribution
- Node:
- Edges encode:
Random Variable
\[P(X_{1:n}) = \prod_{i=1}^n P(X_i \mid \text{pa}(X_i))\]
Full Story: "Causality: Models, Reasoning and Inference" by Judea Pearl
Counting Parameters
For discrete R.V.s:
\[\text{dim}(\theta_X) = \left(|\text{support}(X)|-1\right)\prod_{Y \in Pa(X)} |\text{support}(Y)|\]

Inference
Inputs
- Bayesian network structure
- Bayesian network parameters
- Values of evidence variables
Outputs
- Posterior distribution of query variables

Given that you have detected a trajectory deviation, and the battery has not failed what is the probability of a solar panel failure?
\(P(S=1 \mid D=1, B=0)\)
Exact
Approximate
Exact Inference
Exact Inference

\[P(S{=}1 \mid D{=}1, B{=}0)\]
\[= \frac{P(S{=}1, D{=}1, B{=}0)}{P(D{=}1, B{=}0)}\]
\[P(S{=}1, D{=}1, B{=}0) = \sum_{e, c}P(B{=}0, S{=}1, E{=}e, D{=}1, C{=}c)\]
\[P(B{=}0, S{=}1, E, D{=}1, C)\]
\[= P(B{=}0)\,P(S{=}1)\,P(E\mid B{=}0, S{=}1)\,P(D{=}1\mid E)\,P(C{=}1\mid E)\]
Exact Inference

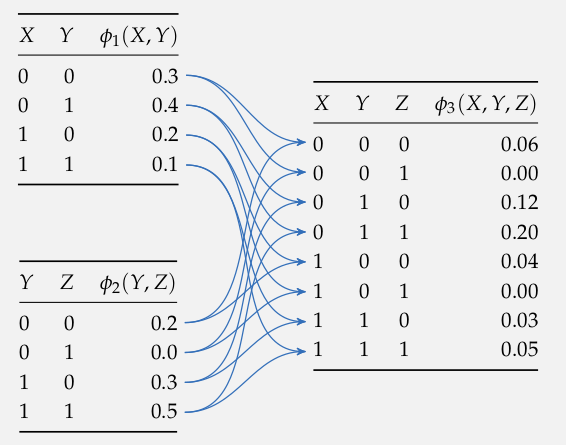
Product
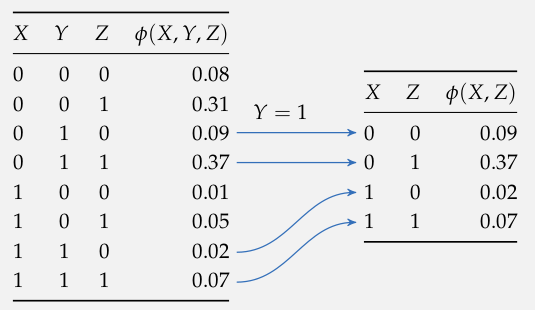
Condition
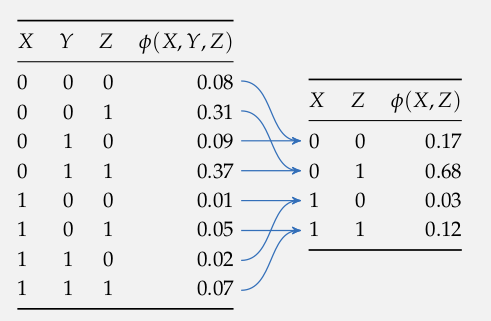
Marginalize

Exact Inference


Exact Inference: Variable Elimination

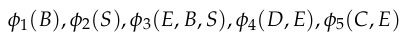
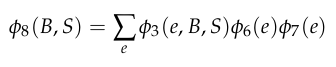
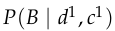
Start with
Eliminate \(D\) and \(C\) (evidence) to get \(\phi_6(E)\) and \(\phi_7(E)\)
Eliminate \(E\)
Eliminate \(S\)
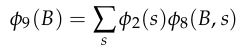
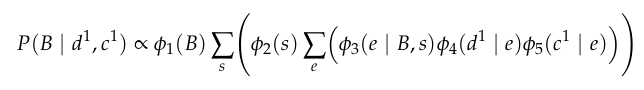
vs
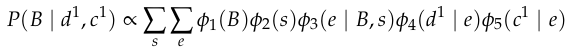
Choosing optimal order is NP-hard
Next Year: Skip
Break
