
Kinodynamic Rollouts and Action Shielding for Intention-Aware Planning
William Pope
M.S. Thesis Defense
14 Nov 2022
Intention-Aware Planning
- Environments with other agents pose a challenge for path planning
- Agents act with intention, but their objectives are not known to others
- By observing past behavior, we can reason about likely future behavior



Pedestrian Problem
- Vehicle needs to navigate around pedestrians/obstacles to reach a goal


- Assumptions:
- Receives measurements of human positions
- Dynamics are deterministic, knows its own state
- Has emergency brake
- Not-at-fault for collisions if stopped
POMDPs
- Partially-observable Markov decision process (POMDP)
- Sequential decision-making framework
- State contains hidden elements
- Belief – probability over possible true states, informed by observations
- For the pedestrian problem:

s = \begin{bmatrix} \text{vehicle state} \\ \text{human positions} \\ \text{human intentions} \end{bmatrix}
o = \begin{bmatrix} \text{vehicle state} \\ \text{human positions} \end{bmatrix}
b = \begin{bmatrix} \text{intention probabilities} \end{bmatrix}
a = \begin{bmatrix} \text{vehicle controls} \end{bmatrix}
Online POMDP Planning
- State/belief space is infinitely large, intractable to solve for global policy
- Online planning:
- Search local area only with forward tree search
- Execute best action, take observation, update belief, repeat search
- POMDP solver is time-constrained by planning frequency


Preceding Work
- Baseline: POMDP speed control [Bai, H. (2015)]
- Tree searches 1D space along pre-planned path
- Rollout: adjust speed along path to avoid humans
- Improved: POMDP speed/steering control [Gupta, H. (2022)]
- Tree searches full state space
-
Rollout: adjust speed to avoid humans and find the goal
- Uses multi-query motion planning to guide rollout


| Holonomic | Nonholonomic | |
| Speed | Bai, H. | Bai, H. |
| Speed/Steering | Gupta, H. |
Planning under Differential Constraints


- Vehicle trajectories must obey equations of motion for dynamical system
- In nonholonomic systems, state evolution is dependent on past states
Holonomic planning
Nonholonomic planning
\dot{x} = f(x, u, t)
Dynamics Model
- Bicycle model with velocity (\(v \geq 0\))
- Inputs: steering, acceleration (discrete set)

x = \begin{bmatrix} x \\ y \\ \theta \\ v \end{bmatrix}
u = \begin{bmatrix} \phi \\ a \end{bmatrix}
\dot{x} = f(x,u) = \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \\ \dot{v} \end{bmatrix} = \begin{bmatrix} v \cos{\theta} \\ v \sin{\theta} \\ v \frac{1}{l}\tan{\phi} \\ a \end{bmatrix}
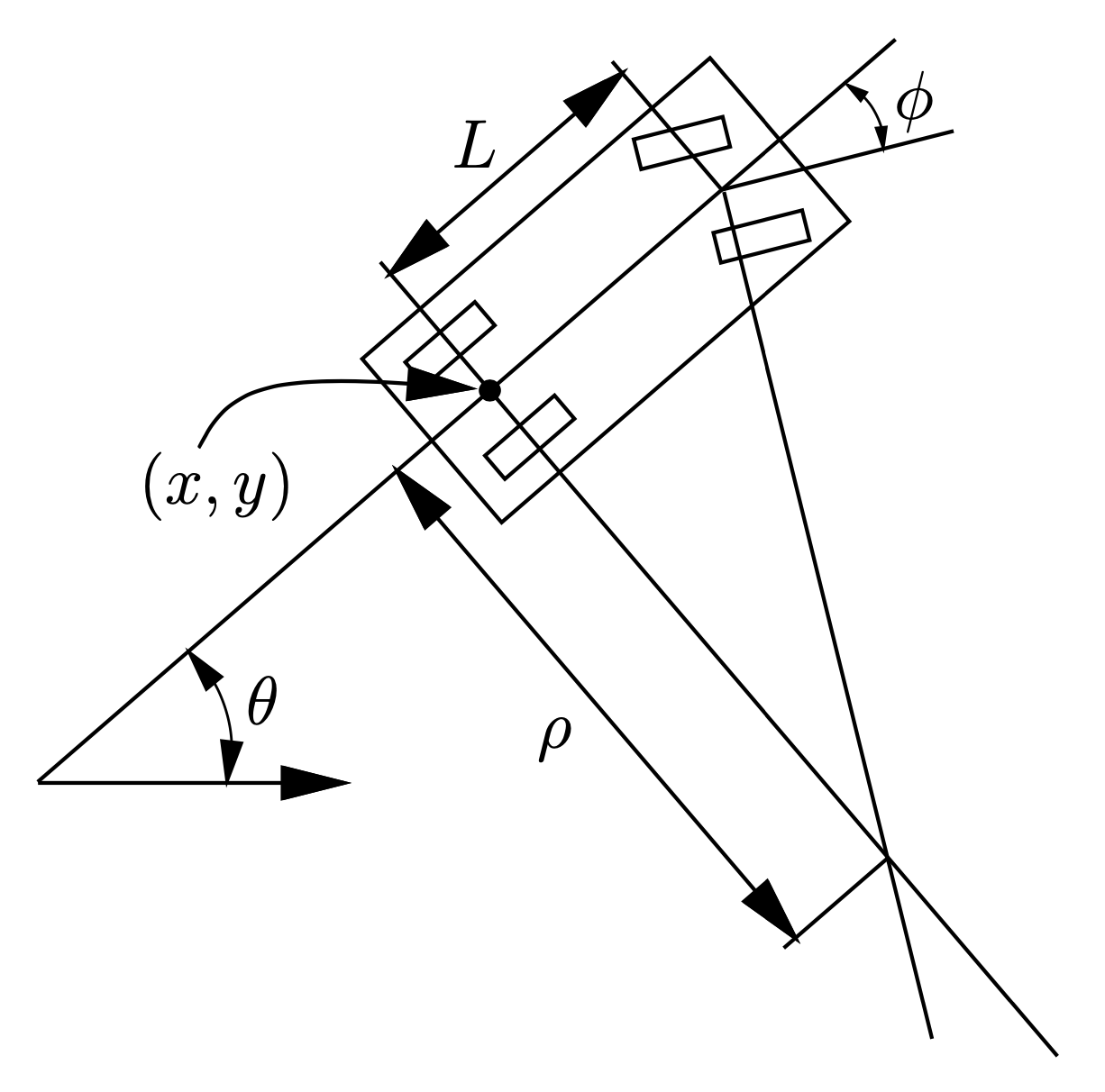
steering limited based on velocity
Contributions and Overview
Contributions
- Extended POMDP planner to nonholonomic vehicles with new rollout policy
- Improved planner safety around pedestrians with online reachability analysis
- Demonstrated planner on new autonomous robot
Overview
- Chapter I: Hamilton-Jacobi-Bellman Rollouts
- Chapter II: Sparse Tree Shielding
- Chapter III: Implementation/Experiments

Chapter I:
Hamilton-Jacobi-Bellman Rollouts

Tree Search Value Estimates
- In online POMDP solvers, need to estimate value of each new node
- Collects information beyond reach of tree
- Value estimates:
- Influence macro scale behavior of planner
- Need to be representative of true POMDP execution/reward


DESPOT Rollout Policies
- In DESPOT, estimate upper/lower bound on value for each node
- UB: simulate path to goal (no humans)
- LB: simulate path to goal (with humans, brake to avoid)
- Requirements:
- Reach goal near-optimally from any state
- Avoid pedestrians along path (lower bound)
- Generate path near instantly
- Follow vehicle dynamics

Goal: create UB/LB rollout policies that meet requirements
Possible Policies
- Random rollout
- Will not find sparse reward in navigation problem
- Graph-based methods
- Difficult to satisfy differential constraints when connecting nodes
- Forward tree search
- Single-query, too slow for online rollouts
- Potential field methods
- Subject to local minima issues, not guaranteed to reach goal
-
Need global optimal control policy
- Hamilton-Jacobi-Bellman equation

Hamilton-Jacobi-Bellman Equation

V(x(t),t) = \max_{u}\{\int_{t}^{t_{f}} R(x(\tau),u(\tau)) d\tau\}
V(x(t),t) = \max_{u}\{\int_{t}^{t+dt} R(x(\tau),u(\tau)) d\tau + V(x(t+dt),t+dt)\}
- Uses dynamic programming to solve Hamilton-Jacobi PDE for optimal control
- Value: optimal reward-to-go from given state/time
- Reformulated with dynamic programming
- With optimal value function, can quickly get optimal control at any state
u^{*}(x(t),t) = \argmax_{u}(Q(x(t),u,t))
0 = \frac{\partial V}{\partial t} + \max_{u}\{\frac{\partial V}{\partial x}\cdot f(x,u) + R(x,u) \}
HJB PDE
Discrete Time HJB

- For discrete time systems, HJB is equivalent to value iteration
V(s) = \max_{a}\{R(s,a) + V(s')\}
- To solve over continuous state space, need to discretize into grid of states \((s)\)
- Next state \((s')\) usually not on grid, so value needs to be interpolated
- Generally requires discrete action set to optimize
Solving for Value Function

- Reward function (same as POMDP)
- if goal: \(R(s) = +1000.0\)
- if obstacle: \(R(s) = -1e6\)
- all actions: \(R(a) = -1.0\)
- Semi-Lagrangian PDE method: compute one-step lookahead at every node until values converge
- Produces \(n\)-dimensional value array
- Can be discontinuous
- Expensive due to dimensionality

Planning with Value Function
- For any state in continuous space, take action that maximizes interpolated Q-value



Faster Planning
- Rollout has sizable impact on POMDP computation cost
- Can speed up policy with offline information
- Exact: interpolates new Q-values for exact continuous state
- Approx: uses stored Q-values from nearest neighbor in state grid


Reactive-HJB Policy
- In order to simulate rollout path with humans, apply reactive acceleration based on distance to nearest human in scenario
- Rollout still needs to reach goal, so reactive controller is coupled with HJB
- RC chooses acceleration
- HJB chooses steering
- If RC accel is unsafe, rollout reverts to pure HJB policy


HJB as Pedestrian Problem Rollout
- Upper bound:
- Use exact HJB policy to simulate optimal human-free path
- Runs once per node
- Lower bound:
- Use approximate reactive policy to simulate path avoiding humans
- Runs once per scenario per node

Rollout Policy Comparison

- Lower bound policies reach goal, regardless of reactive acceleration input


| Policy | Runtime [μs] |
|---|---|
| HJB | 18.064 |
| Reactive-HJB | 6.083 |
| Approx Reactive-HJB | 1.915 |
|A| = 21,
|A_{RC}| = 7
POMDP w/ HJB Rollouts


Performance by Rollout Choice

- No significant difference observed for faster lower bound policy
- Any improvement in tree size may be negated by looser bound
| Lower Bound Policy | Average Time-to-Goal [s] | Average Node Rate [1/s] |
|---|---|---|
| Reactive-HJB | 17.9 | 759.4 |
| Approx Reactive-HJB | 16.5 | 820.0 |
N = 10
Chapter II:
Sparse Tree Shielding

Pedestrian Collision Avoidance
- Future human collisions are predicted/penalized in POMDP tree
- However,
- DESPOT explores finite number of observation branches
- Collision penalty may be washed out by nearby safe nodes
- Vehicle assumed to have instant emergency brake

Goal: add safety mechanism to handle low probability collisions and finite braking ability

Ye, N., et al
Reach-Avoid Games
- Players:
- Vehicle (P1) wants to reach goal
- Humans and obstacles (P2) "want" to cause collisions
- At a given state:
- Vehicle wins if there exists a safe path to goal in finite time
- Obstacles win if all of vehicle's future paths can be blocked
- To ensure vehicle safety, must only visit states with known safe future paths


[Chen, M.]
Human Reachable Set
- Vehicle path is not safe if it intersects human's reachable set in space/time
- Approximating human FRS:
- From observation, propagate human toward all possible goals
- Define FRS as convex hull of states at each time step





Vehicle Safe Set
- Vehicle has two known invariant safe sets:
- In goal
- In free space with zero velocity (not at fault)
- For any other state to be safe, must have a path to these sets that does not intersect obstacles or human FRS
- Only need to prove existence of one such path
- More simply: vehicle must be able to safely stop from any visited state


Online Action Shielding
- DESPOT produces Q-values for all actions at \(t_{k+1}\)
- Shield filters out actions with human FRS intersections prior to \(t_{stop}\)
- Agent executes best action from remaining safe action set

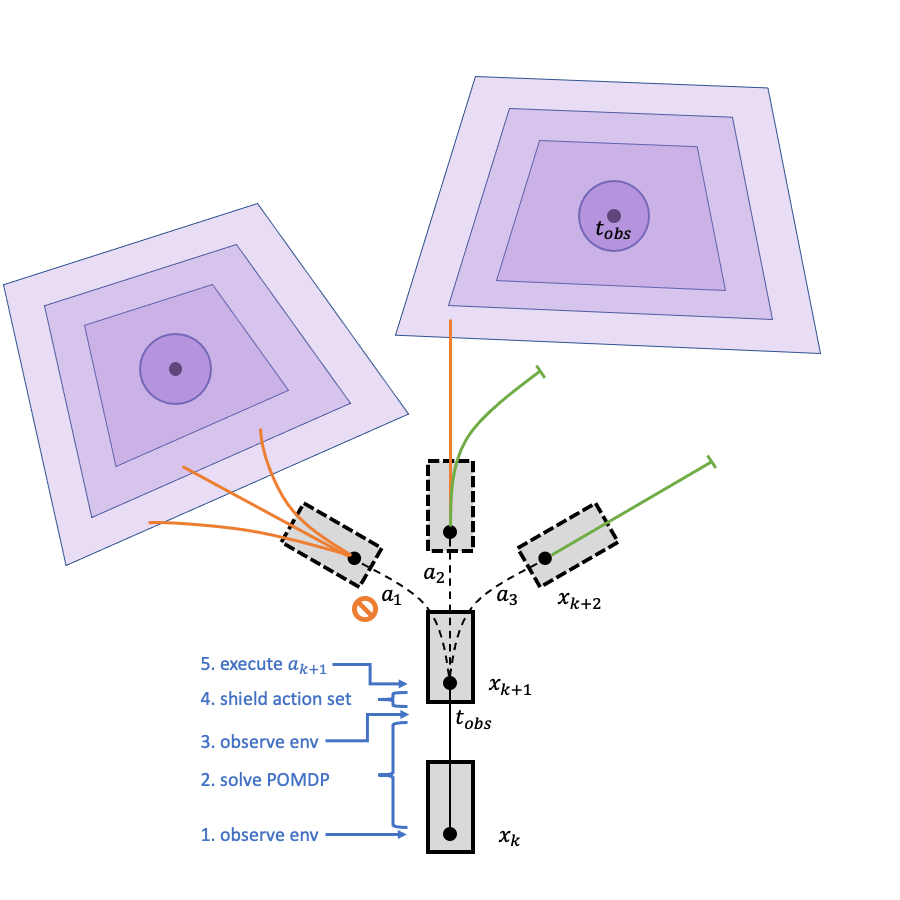
POMDP w/ Shield


Performance

| Humans in Environment | Average Time-to-Goal [s] | Interventions / Actions | Collisions / Trials |
|---|---|---|---|
| 10 (off) | 15.4 | n/a | 0.1 |
| 10 (on) | 23.0 | 0.207 | 0 |
| 20 (off) | 17.2 | n/a | 0.2 |
| 20 (on) | 31.3 | 0.280 | 0 |
- Shield is able to prevent collisions, but at significant time cost
N = 10
Chapter III.a:
Experimental Robot

Marmot
- Built car-like robot to test planners in real-time/real-world environment
- Runs POMDP planner on-board
- Collects state data from motion capture system


Hardware
- Based on F1Tenth open-source design
- Modified for ADCL uses
- Larger computer, dual batteries, more sensor mounts



Hardware stack
Intel NUC i5
Software

- Using ROS1
- POMDP implemented in Julia (RobotOS.jl)
- Planner and belief updater in separate nodes
- Minimal integration effort for new planners

Online decision loop
\(f_{loop} = 2 \text{ Hz}\)
POMDP-ROS Demonstration

Chapter III.b:
BellmanPDEs.jl

BellmanPDEs.jl

- Created Julia package for HJB solver/planner
- Intended for standalone planning or POMDP rollouts


Conclusion

- HJB rollout enables use of planner in broader applications
- Action shielding provides safety while preserving planner behavior
Future work
- Implement more efficient HJB solvers for larger environments
- Add disturbances and low level controller to vehicle dynamics
- Include more social context in humans/planner
Questions


William Pope
Copy of Thesis
By Zachary Sunberg
Copy of Thesis
- 705



