POMDP Planning for Optimized ALD Deployment

Himanshu Gupta

Zachary Sunberg

University of Colorado Boulder

Types of Uncertainty

OUTCOME

MODEL

STATE

Markov Model

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}\) - Transition probability distributions

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Solving MDPs - The Value Function

$$V^*(s) = \underset{a\in\mathcal{A}}{\max} \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$

Involves all future time

Involves only \(t\) and \(t+1\)

$$\underset{\pi:\, \mathcal{S}\to\mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, \pi(s_t)) \bigm| s_0 = s \right]$$

$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$

Value = expected sum of future rewards

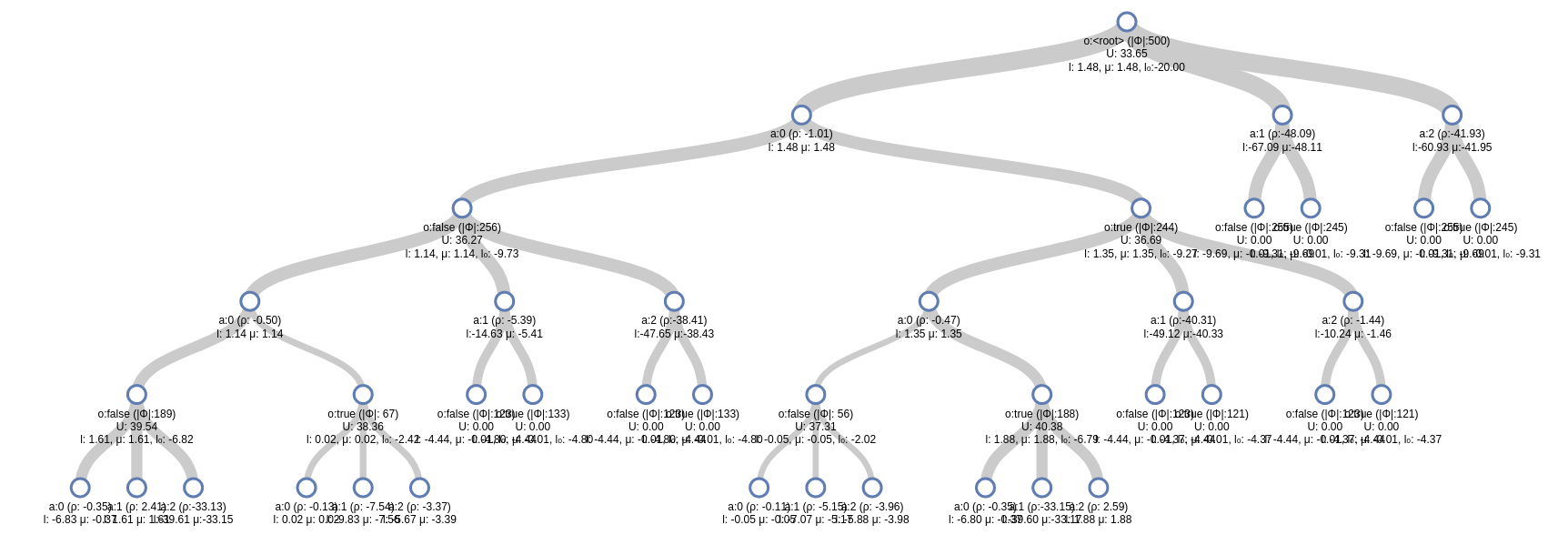
Online Decision Process Tree Approaches

Time

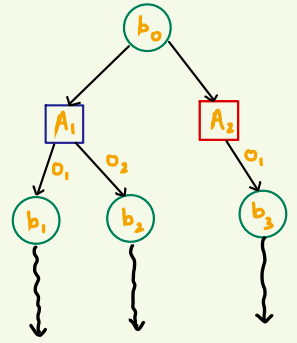
Estimate \(Q(s, a)\) based on children

$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$

\[V(s) = \max_a Q(s,a)\]

$$Q(b,a) = \rho(b, a) + \gamma \mathop{\mathbb{E}}_{b' \sim \mathbb{B}}\Big[V(b') \mid b, a\Big]$$

\[V(b) = \max_{a \in A} Q(b,a)\]

$$Q(b,a) = \rho(b, a) + \gamma \Big[\sum_{o \in \mathbb{O}} P(o|b,a) * V(\tau(b,a,o))\Big] $$

$$Q(b,a) = \rho(b, a) + \gamma \underset {o \sim Z(b,a)} \mathbb{E} \Big[V(\tau(b,a,o))\Big] $$

$$\rho(b,a) = -H(b) + R(b,a)  $$

\[V(b) = \max_{a \in A} Q(b,a)\]

$$\rho(b,a) = -H(b) + R(b,a)  $$

\[V(b) = \max_{a \in A} Q(b,a)\]

$$\rho(b,a) = -H(b) + R(b,a)  $$

$$Q(b,a) = \rho(b, a) + \gamma \underset {o \sim Z(b,a)} \mathbb{E} \Big[V(\tau(b,a,o))\Big] $$

\[V(b) = \max_{a \in A} Q(b,a)\]

Partially Observable Markov Decision Process (POMDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
  • \(\mathcal{O}\) - Observation space
  • \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution
\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

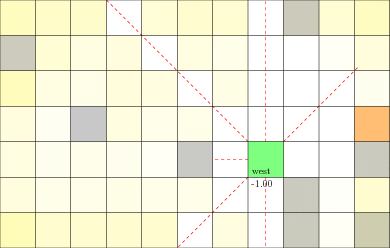
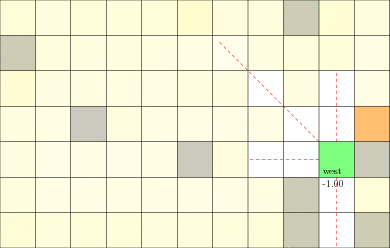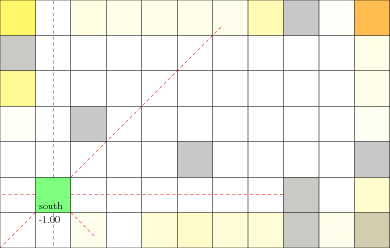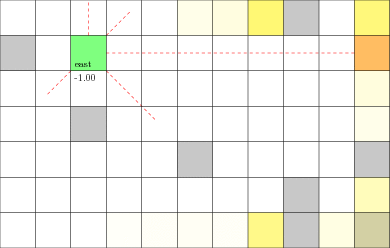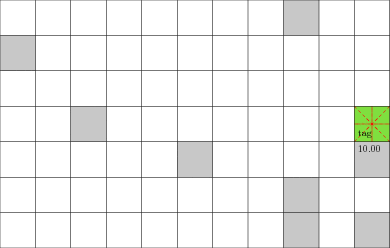
Accurate Observations

Goal: \(a=0\) at \(s=0\)

Optimal Policy

Localize

\(a=0\)

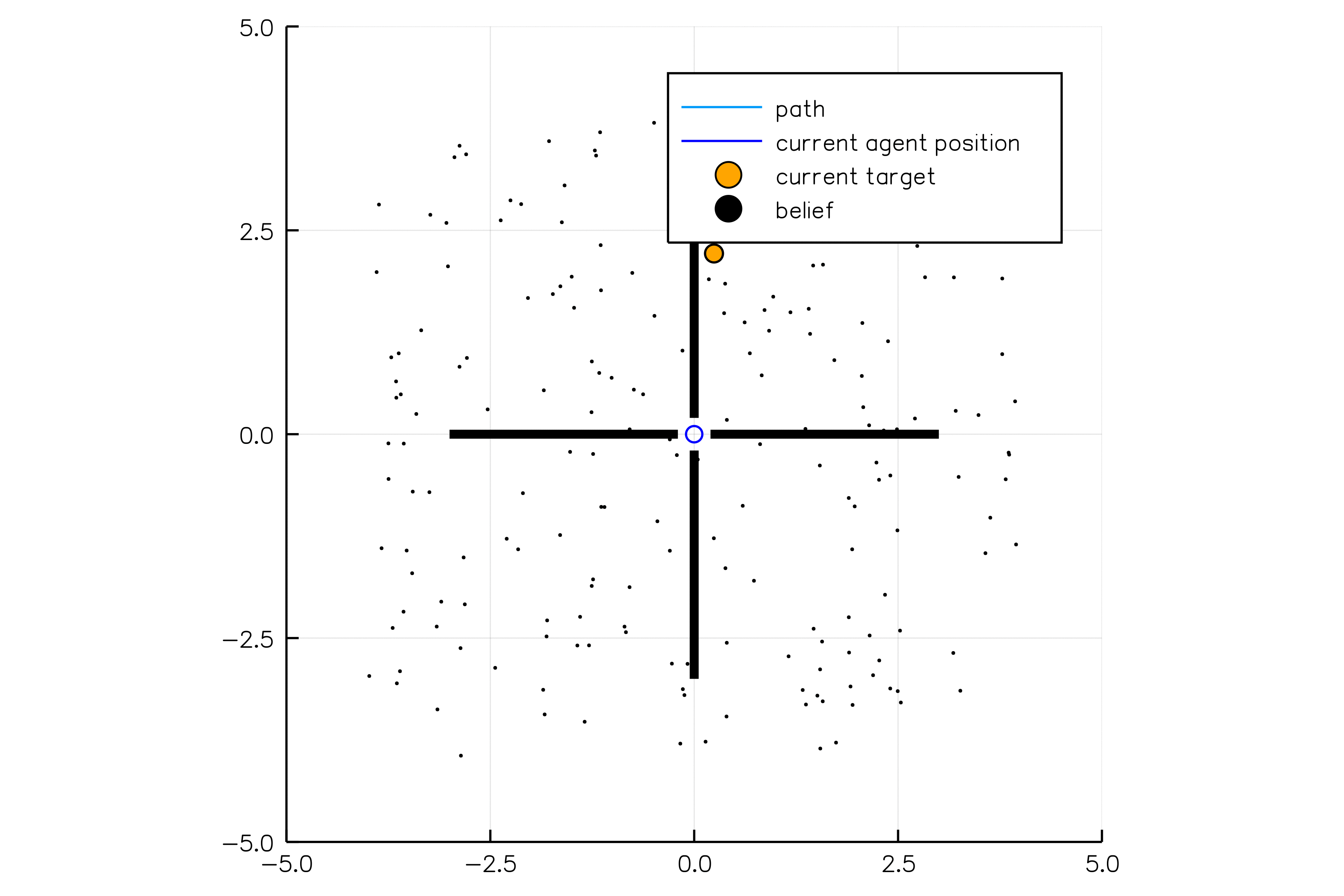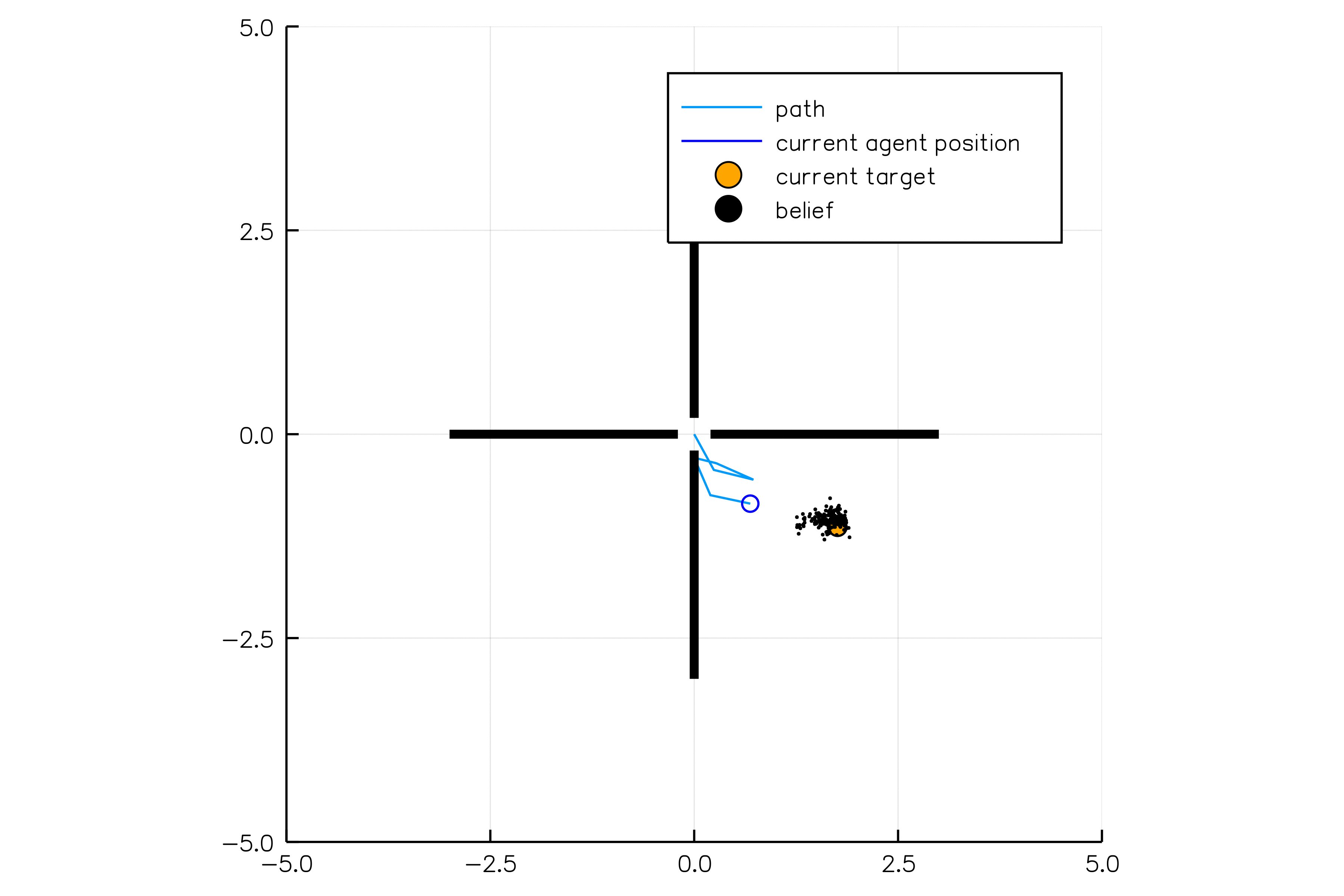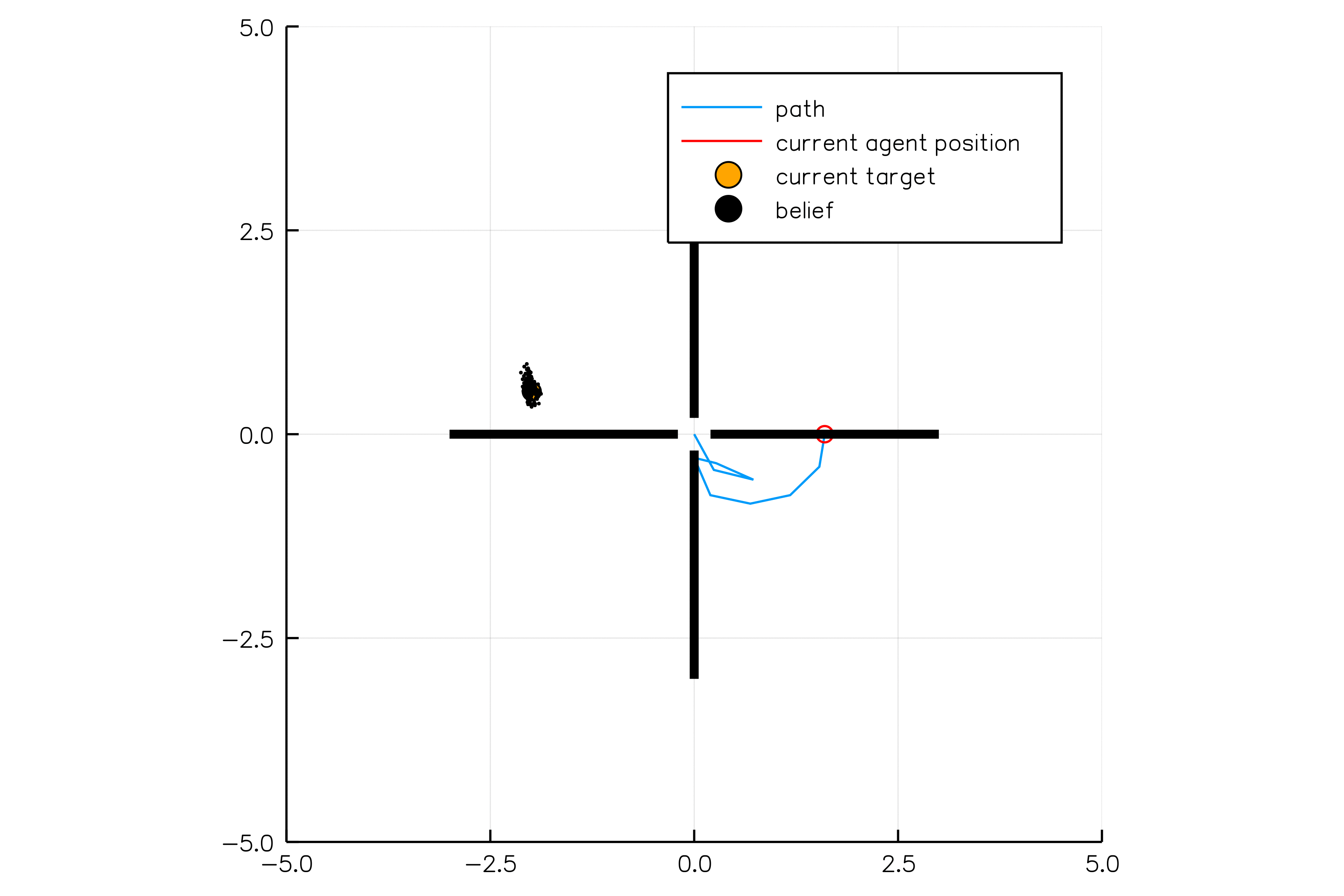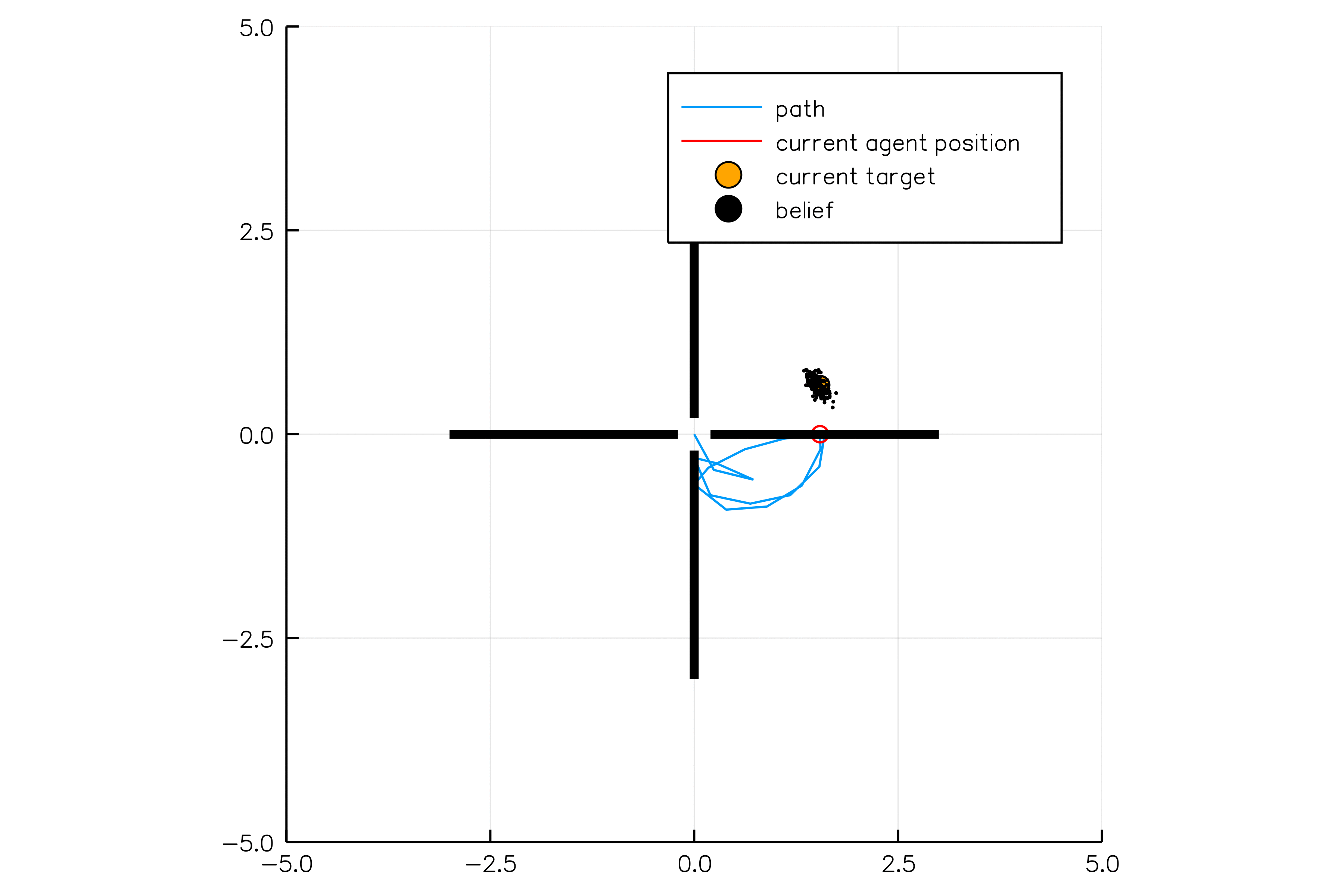
POMDP Example: Light-Dark

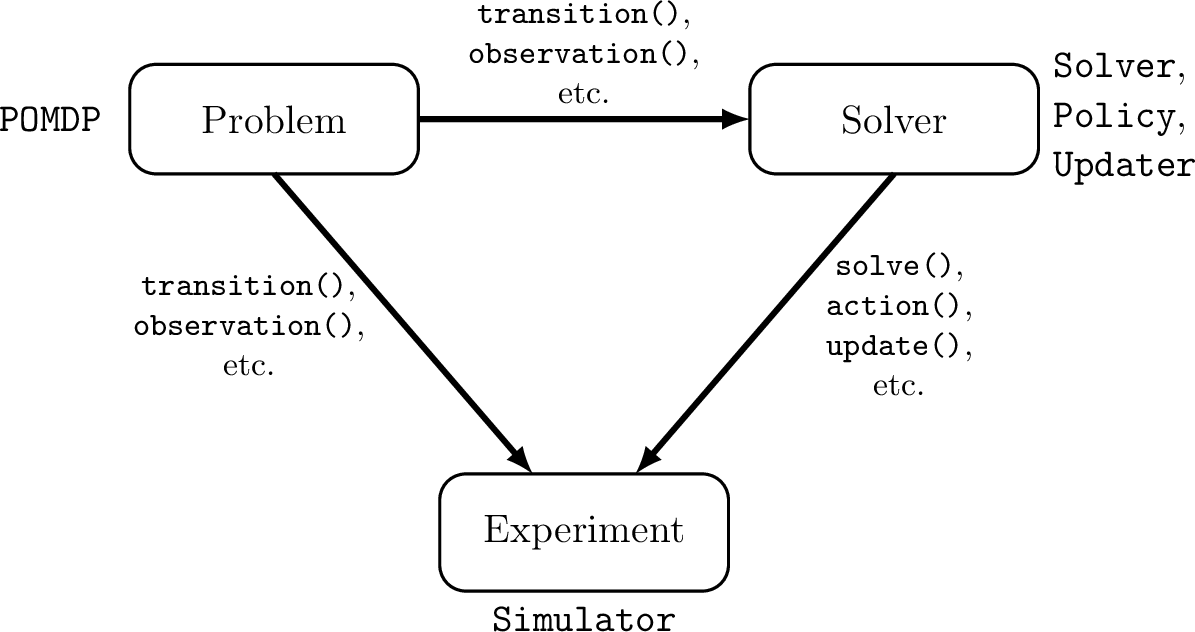
POMDP Sense-Plan-Act Loop

Environment

Belief Updater

Policy

\(b\)

\(a\)

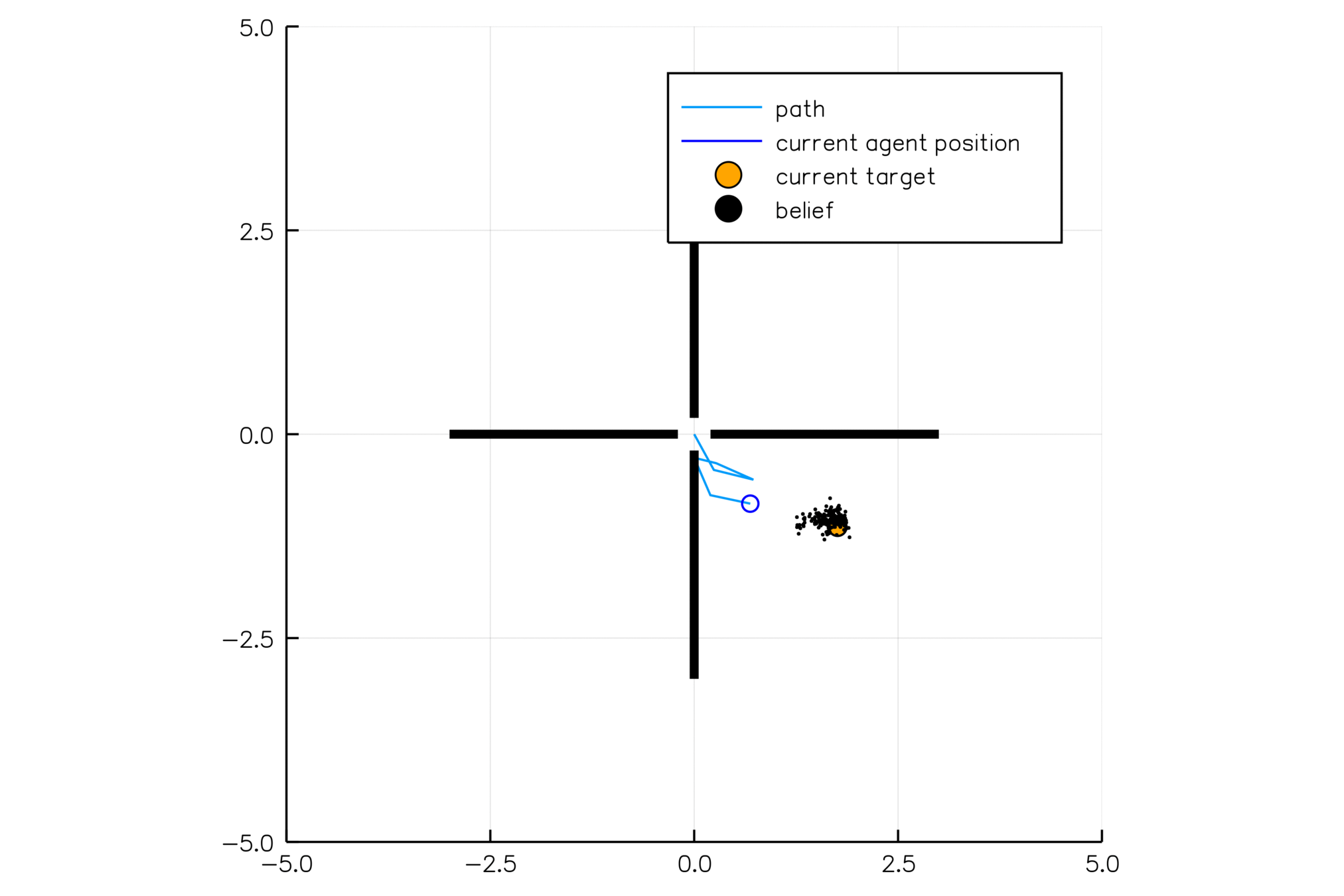
\[b_t(s) = P\left(s_t = s \mid a_1, o_1 \ldots a_{t-1}, o_{t-1}\right)\]

True State

\(s = 7\)

Observation \(o = -0.21\)

Questions?

POMDP

  • A POMDP is an MDP over the belief space.
     
  • Goal: Find a policy that maximizes
     $$E\left[\sum_{t=0}^{\infty} \gamma^t R(b_t, \pi(b_t)) \bigm| b_0 \right]$$
     
  • For ALD deployment, the goal is to find a policy that minimizes
     $$E\left[H(b_T) \bigm | b_0,\pi \right]$$
    where \(H\) is the measure of uncertainty in any given belief

Information Space Planning as a \(\rho\)-POMDP

  • STATES :  (State of the atmosphere, State of the aircraft, State of all the drifters)

    $$\mathcal{s(t)} = ( \mathbb{ \eta(t)}, x(t), \xi_1(t), \xi_2(t),...,\xi_m(t) )$$
  • ACTIONS :  All possible 10-minute trajectories with possible ALD drop points.
     
  • OBSERVATIONS :  Measurements from all the sensors, i.e. sensors on the aircraft, ground vehicle and drifters.
     
  • BELIEF: A set of weather models and their respective likelihoods (assume aircraft and drifter states are known).

Connection to OSSE!

OSSE is similar to a 1-step POMDP

LAST TIME

  • POMDP is a problem formulation where r denotes the reward obtained by executing an action a in state s.

     
  • \(\rho\)-POMDP is another problem formulation where \(\rho\) denotes the reward obtained by executing action a at belief b.

     
  • Family of solution techniques for solving these POMDPs - tree search planning.

Solving a POMDP

  • Obtaining exact solutions to POMDPs is an intractable problem [1].
     
  • They are solved approximately in an online fashion by performing a tree search over the belief space.

[1] Christos H. Papadimitriou and John N. Tsitsiklis. 1987. The Complexity of Markov Decision Processes. Mathematics of Operations Research 12, 3 (1987), 441–450.

Action Nodes

Belief Nodes

  • A POMDP is an MDP on the Belief Space but belief updates are expensive.
     
  • POMCP* uses simulations of histories instead of full belief updates
     
  • Each belief is implicitly represented by a collection of either unweighted or weighted particles

[Ross, 2008] [Silver, 2010]

*(Partially Observable Monte Carlo Planning)

Solving a POMDP

Desired Policy

  • Goal: Reach a belief that has less uncertainty about the atmosphere.

     
  • Policy: Find actions that lead to regions of the belief space with less uncertainty. 

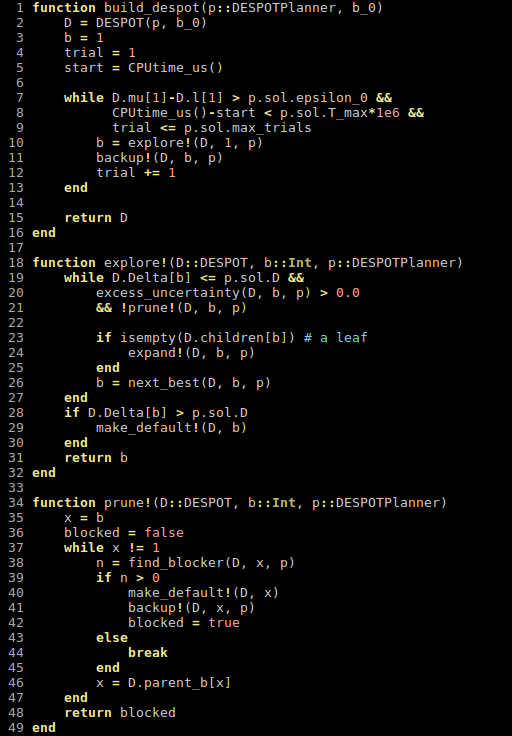
Solving a POMDP using DESPOT-\(\alpha\)

  • Number of nodes in a belief tree of height D --> \(O (|A|^D |Z|^D\))
    • |A| - size of the action set
    • |Z| - size of the observation set
    • Blows up as the planning horizon increases.

       
  • Efficient fix - Summarize the execution of all policies under a fixed number of sampled scenarios.
    • Scenario is a tree with fixed disturbances for transitions and observations.
    • All random disturbances for a scenario are chosen before hand.

DESPOT - \(\alpha\)

  • Tree constructed using K sampled scenarios has \(O (|A|^D K\)) nodes
    • Computationally efficient for small K.
    • Theoretical guarantees that a small number of samples is enough to generate a good estimate.

       
  • Scenario = (weather model/forecast, a sequence of fixed disturbances)

Challenges in solving the defined \(\rho\)-POMDP

  1. SOTA Online POMDP solvers don't work well for large or continuous action spaces.
     
  2. A belief tree grows exponentially with depth D
    • Choose good branches to explore within the limited time (using UB and LB).

PROPOSED SOLUTION: Both these problems can be solved using some initial seed of "sensitive" regions to explore which can be obtained from ESA.  

Lower and Upper bounds

  • Tree search in DESPOT-\(\alpha\) is guided by a lower bound and an upper bound on the value estimates at each belief node.
     
  • The lower bound is generally obtained by executing a roll-out policy.
    • Collaborate with Dr. Frew's group.
       
  • The upper bound can be obtained by overestimation.
    • Most naive option is 0

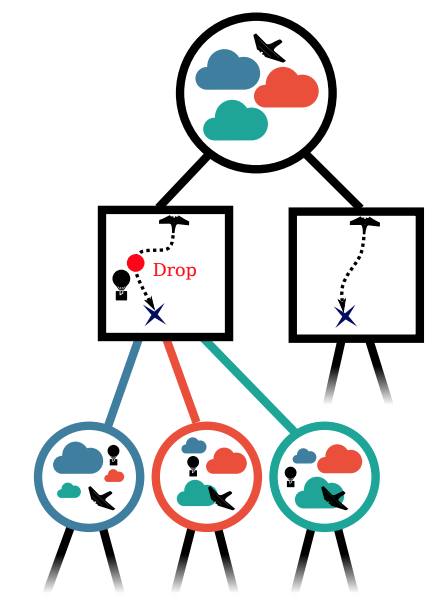
Proposed Approach #1

  • Use the ESA techniques to identify sensitive regions

     
  • Back-propagate the paths of drifters from those regions using existing models

     
  • Choose deployment points along the predicted drifter paths.

Proposed Approach #1

Proposed Approach #2

  • Use the ESA techniques to identify sensitive regions.
     
  • Find the path for the UAV from its current position to those sensitive regions.
     
  • Choose deployment points along the generated paths.

Questions?

Information-Space Planning for ALD Deployment

\(E \sum R(s, a)\)

\(O (|A|^D |Z|^D\))

 \(O\) 

\(O (|A|^D |Z|^D\))

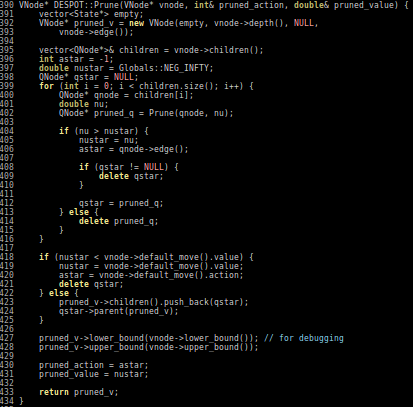
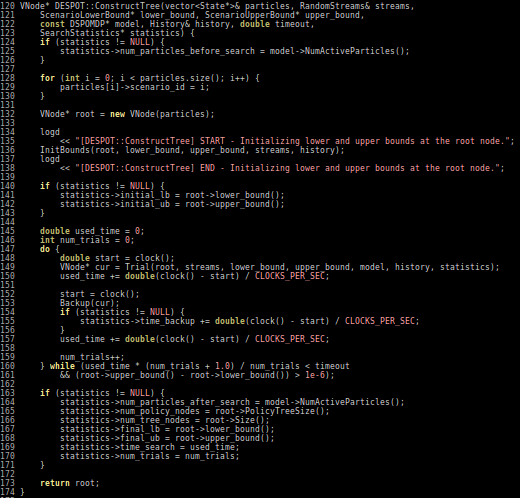
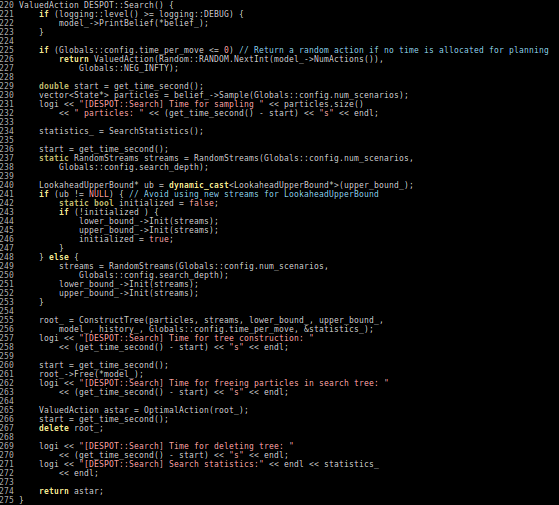
  • Introducing POMDPs; Hard to solve completely, and so solved approximately using online tree search-based solvers.
  • TL;DR version of DESPOT and how it samples K scenarios 
  • Talk about DESPOT-alpha?
  • Information Space Planning
  • What's the action space for the POMDP?
  • The action space also defines the roll-out policy. Possible options?
  • How we plan to use DESPOT-alpha to solve the problem?

Connection to OSSE!

OSSE is just a 1-step POMDP

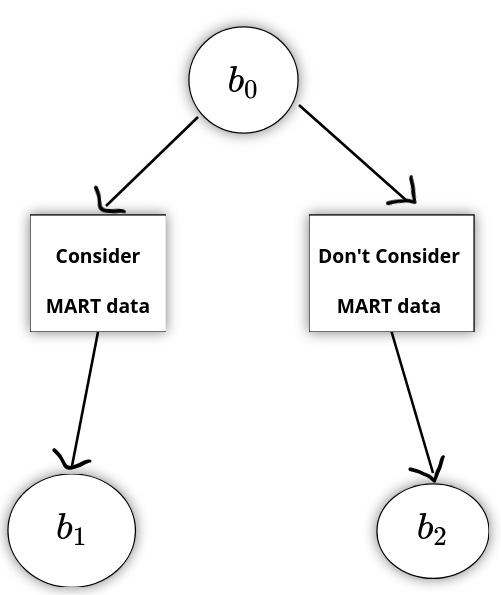
\(b_0\)

\(b_1\)

\(b_2\)

Consider MART data

Don't Consider MART data

Desired Policy

  • Goal: Reach a belief that has less uncertainty about the atmosphere.

     
  • Policy: Find actions that lead to regions of the belief space with less uncertainty. 

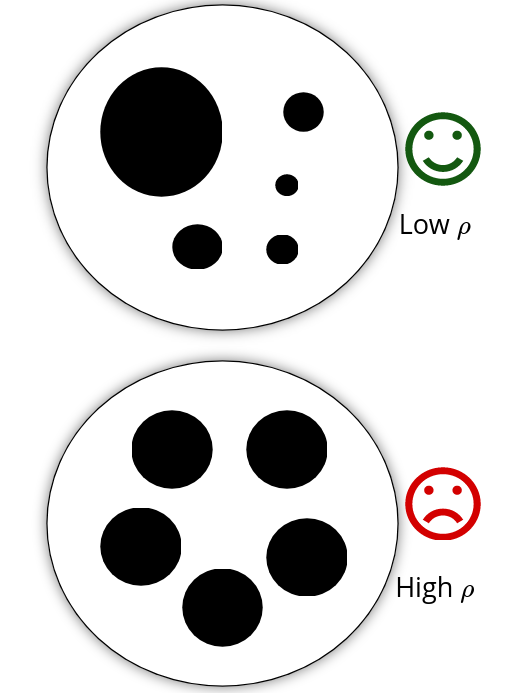
Low \(\rho\)

High \(\rho\)

Challenges in solving the defined POMDP

  1. SOTA Online POMDP solvers don't work well for large or continuous action spaces.
     
  2. A complete belief tree grows exponentially with the depth D
    • Choose good branches to explore within the limited time (using UB and LB).

PROPOSED SOLUTION: Both these problems can be solved using some initial seed of "sensitive" regions to explore which can be obtained from ESA.  

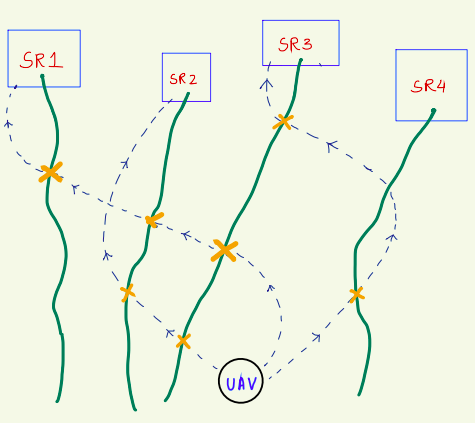
Proposed Approach #1

  • Use the ESA techniques to identify sensitive regions

     
  • Back-propagate the paths of drifters from those regions using existing models

     
  • Choose deployment points along the predicted drifter paths.

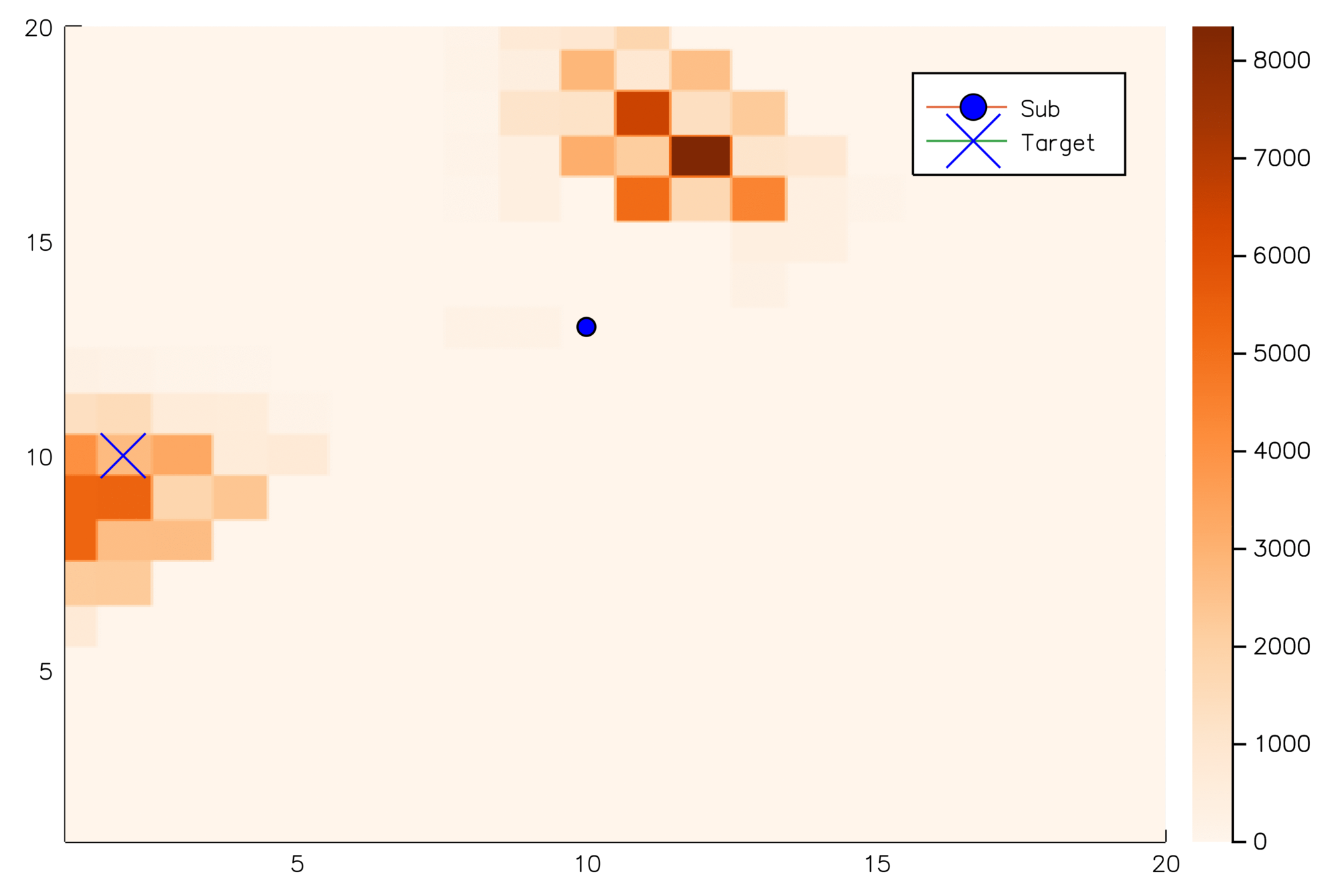
SR1

SR2

SR3

SR4

SR3

UAV

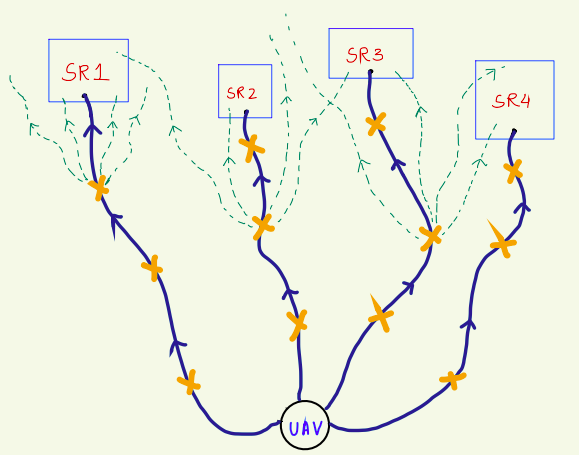
Proposed Approach #2

  • Use the ESA techniques to identify sensitive regions.

     
  • Find the path for the drifter from its current position to those sensitive regions,

     
  • Choose deployment points along the predicted paths.

SR1

SR2

SR3

SR4

SR3

UAV

image/svg+xml

Autorotation

Driving

POMDPs

POMCPOW

POMDPs.jl

Future

POMDP Sense-Plan-Act Loop

Environment

Belief Updater

Policy

\(o\)

\(b\)

\(a\)

  • A POMDP is an MDP on the Belief Space but belief updates are expensive
  • POMCP* uses simulations of histories instead of full belief updates
  • Each belief is implicitly represented by a collection of unweighted particles

[Ross, 2008] [Silver, 2010]

*(Partially Observable Monte Carlo Planning)

 

[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

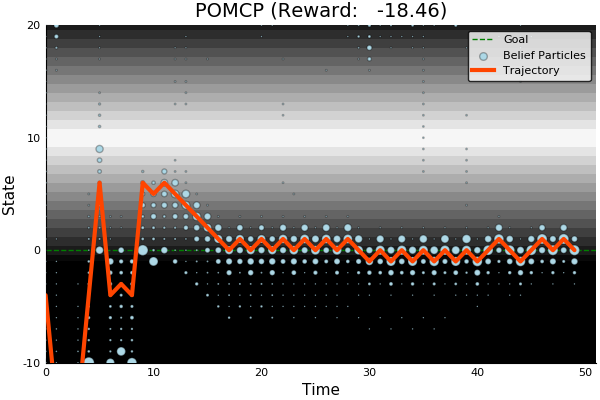
Solving continuous POMDPs - POMCP fails

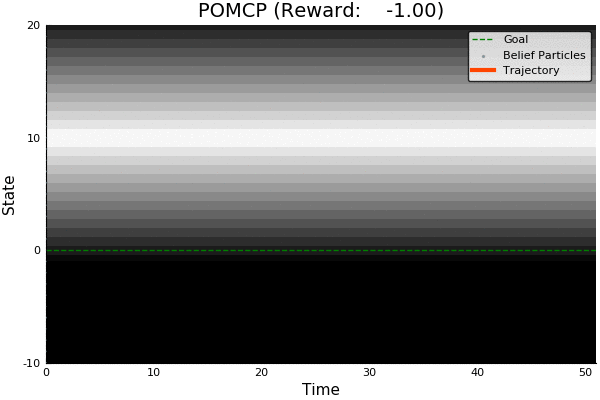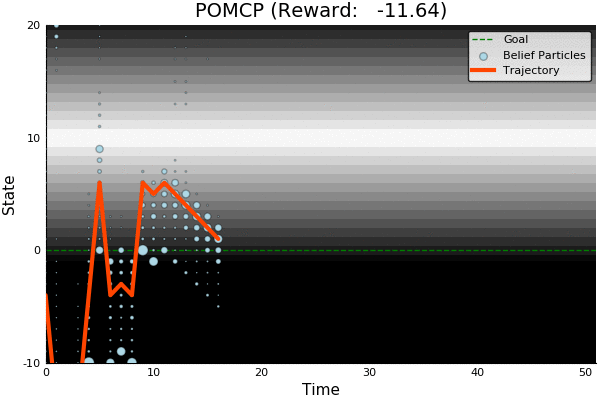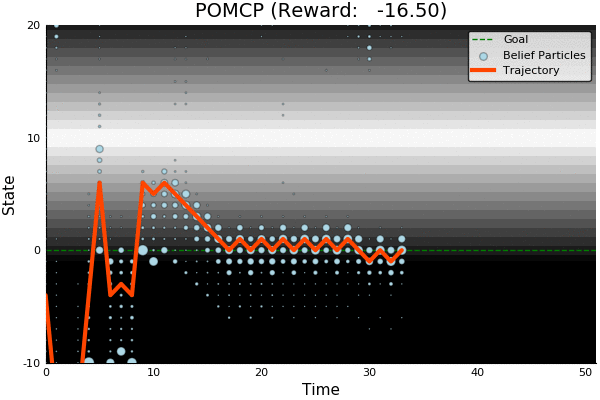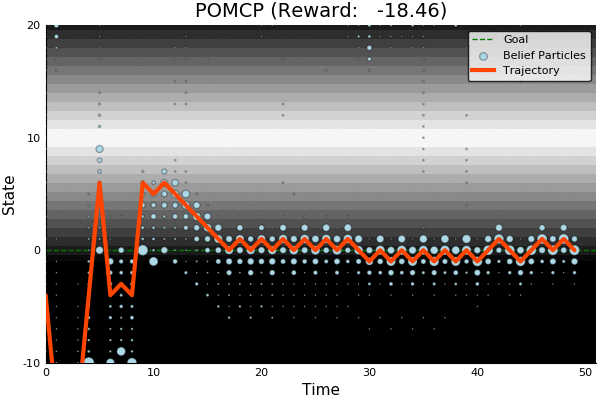
POMCP

✔

✔

Double Progressive Widening (DPW): Gradually grow the tree by limiting the number of children to \(k N^\alpha\)

Necessary Conditions for Consistency

 

[Coutoux, 2011]

POMCP

POMCP-DPW

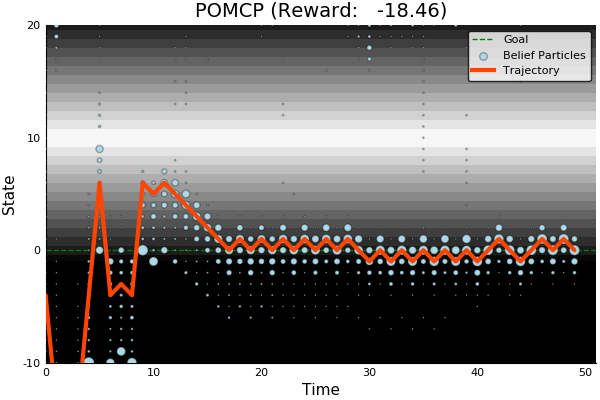
[Sunberg, 2018]

POMDP Solution

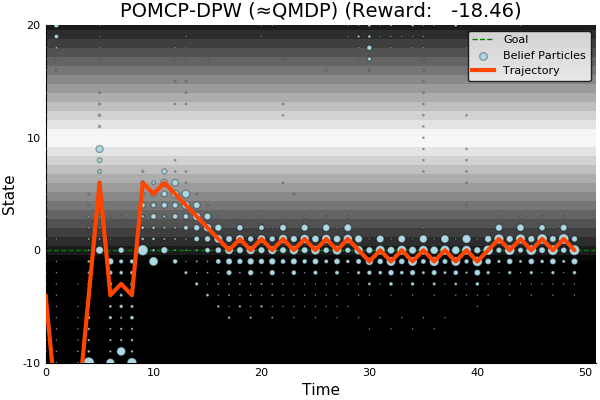
QMDP

\[\underset{\pi: \mathcal{B} \to \mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(b)\]

\[\underset{a \in \mathcal{A}}{\mathop{\text{maximize}}} \, \underset{s  \sim{} b}{E}\Big[Q_{MDP}(s, a)\Big]\]

Same as full observability on the next step

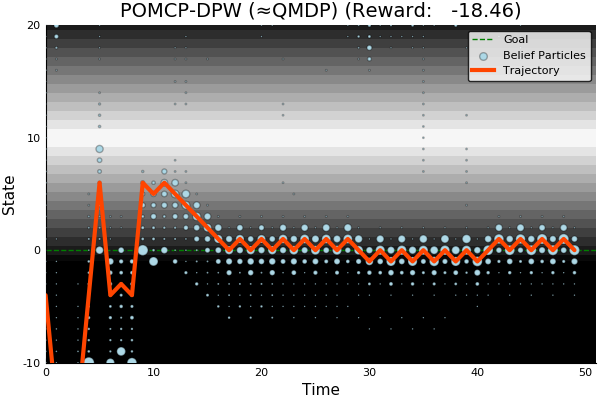
POMCP-DPW converges to QMDP

Proof Outline:

  1. Observation space is continuous with finite density → w.p. 1, no two trajectories have matching observations


  2. (1) → One state particle in each belief, so each belief is merely an alias for that state


  3. (2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state


  4. Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP


    5.  

[Sunberg, 2018]

POMCP-DPW

 

[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

[  ] An infinite number of particles must be added to each belief node

✔

✔

Necessary Conditions for Consistency

 

Use \(Z\) to insert weighted particles

✔

[Sunberg, 2018]

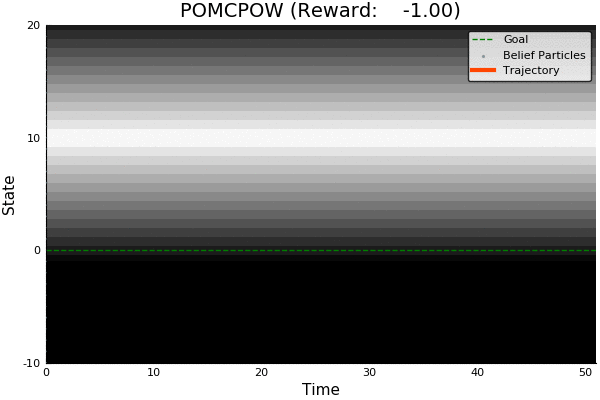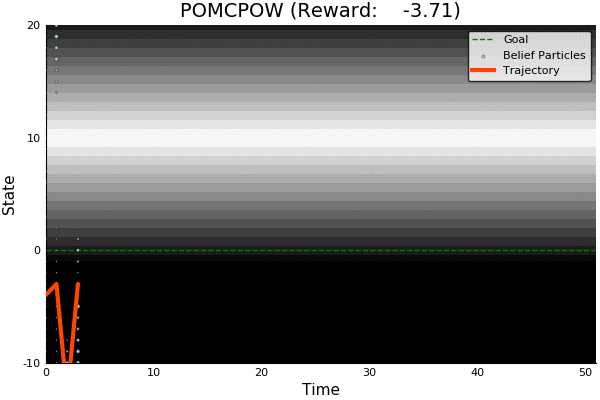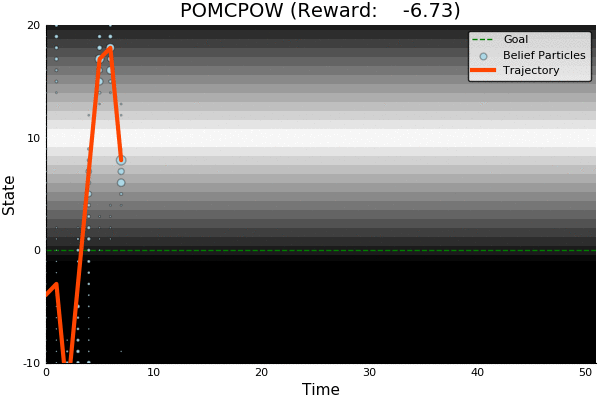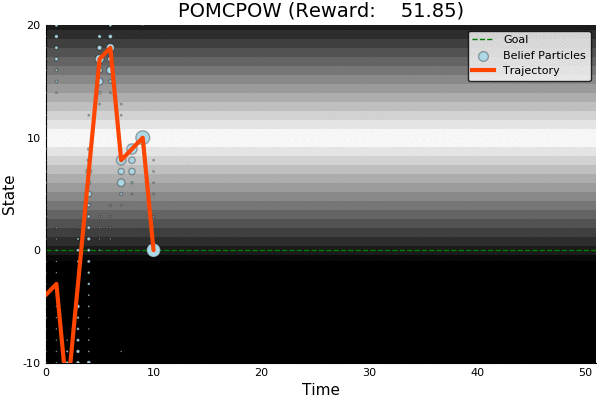
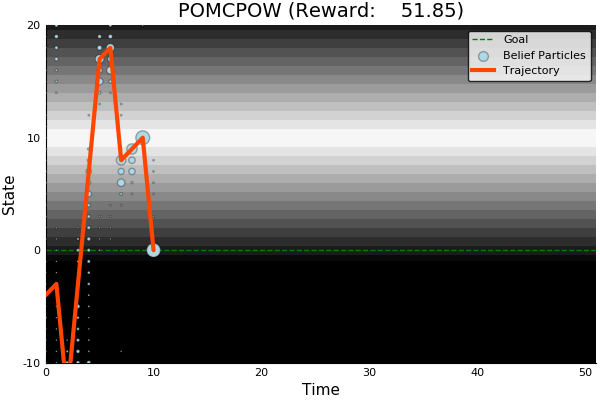
POMCP

POMCP-DPW

POMCPOW

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Ye, 2017] [Sunberg, 2018]

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Next Step: Planning on Weighted Scenarios

image/svg+xml

Autorotation

Driving

POMDPs

POMCPOW

POMDPs.jl

Future

POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

[Egorov, Sunberg, et al., 2017]

Challenges for POMDP Software

  1. POMDPs are computationally difficult.

Julia - Speed

Celeste Project

1.54 Petaflops

Challenges for POMDP Software

  1. POMDPs are computationally difficult.
  2. There is a huge variety of
    • Problems
      • Continuous/Discrete
      • Fully/Partially Observable
      • Generative/Explicit
      • Simple/Complex
    • Solvers
      • Online/Offline
      • Alpha Vector/Graph/Tree
      • Exact/Approximate
    • Domain-specific heuristics

Explicit

Black Box

("Generative" in POMDP lit.)

\(s,a\)

\(s', o, r\)

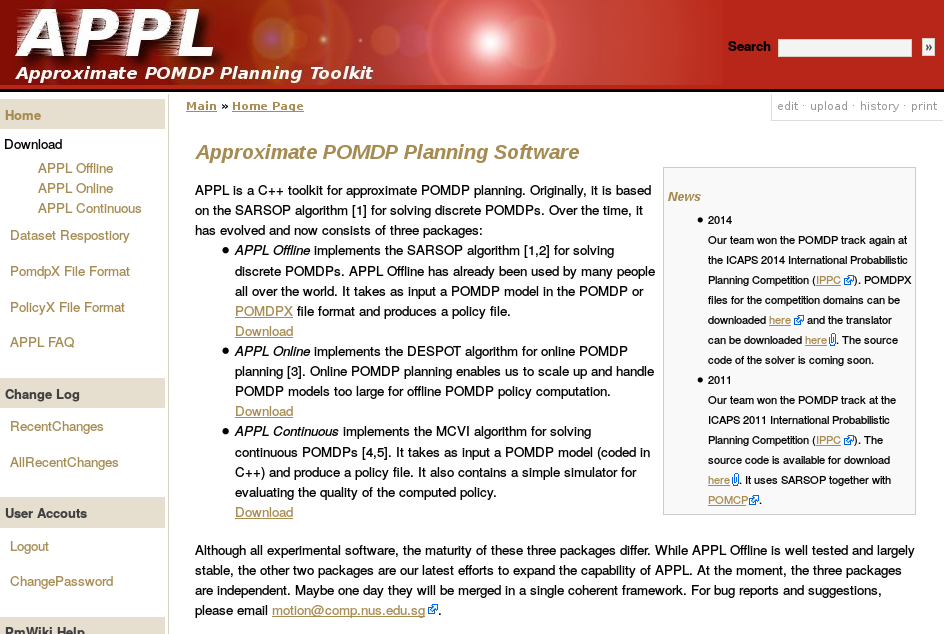
Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

[Egorov, Sunberg, et al., 2017]

image/svg+xml

Autorotation

Driving

POMDPs

POMCPOW

POMDPs.jl

Future

Future Research

Deploying autonomous agents with confidence

Practical Safety Gaurantees

Trusting Visual Sensors

Algorithms for Physical Problems

Physical Vehicles

Trusting Information from Visual Sensors

Environment

Belief State

Convolutional Neural Network

Control System

Architecture for Safety Assurance

Algorithms for the Physical World

1. Continuous multi-dimensional action spaces

2. Data-driven models on modern parallel hardware

image/svg+xml

CPU Image By Eric Gaba, Wikimedia Commons user Sting, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=68125990

3. Better algorithms for existing POMDPs

  • Health screening
  • Human-robot interaction

Practical Safety Guarantees

  • Reachability-based guarantees are usually infeasible
  • Probabilistic guarantees involve low-probability distribution tails

Physical Vehicles in the Real World

Texas A&M (HUSL)

RC Car with assured visual sensing

Optimized Autorotation

Active Sensing

New Course: Decision Making Under Uncertainty

Project-Centric

1. Intro to Probabilistic Models

2. Markov Decision Processes

3. Reinforcement Learning

4. POMDPs

(More focus on online POMDP solutions than Stanford course)

Acknowledgements

The content of my research reflects my opinions and conclusions, and is not necessarily endorsed by my funding organizations.

Thank You!

zachary.sunberg.net

image/svg+xml

POMDP Formulation

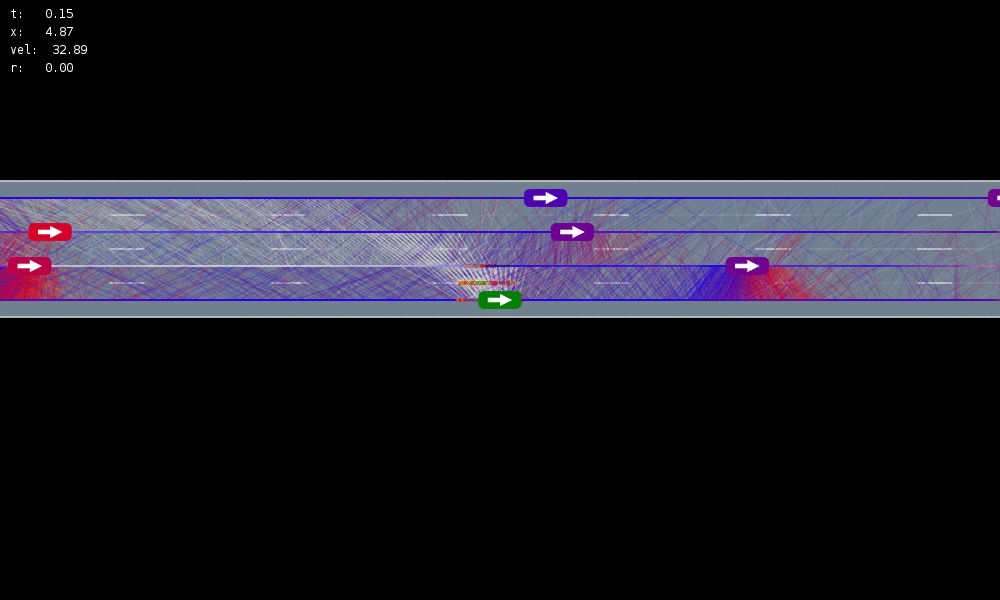
\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states of other cars

  • Actions filtered so they can never cause crashes
  • Braking action always available

Efficiency

Safety

$$R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)$$

POMDPs in Aerospace

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\)

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states

Efficiency

Safety

\( - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)\)

\(R(s, a, s') = \text{in\_goal}(s')\)

[Sunberg, 2017]

"[The autonomous vehicle] performed perfectly, except when it had to merge onto I-395 South and swing across three lanes of traffic"

- Bloomberg

http://bloom.bg/1Qw8fjB

Monte Carlo Tree Search

Image by Dicksonlaw583 (CC 4.0)

image/svg+xml

Autorotation

Driving

POMDPs

POMCPOW

POMDPs.jl

Future

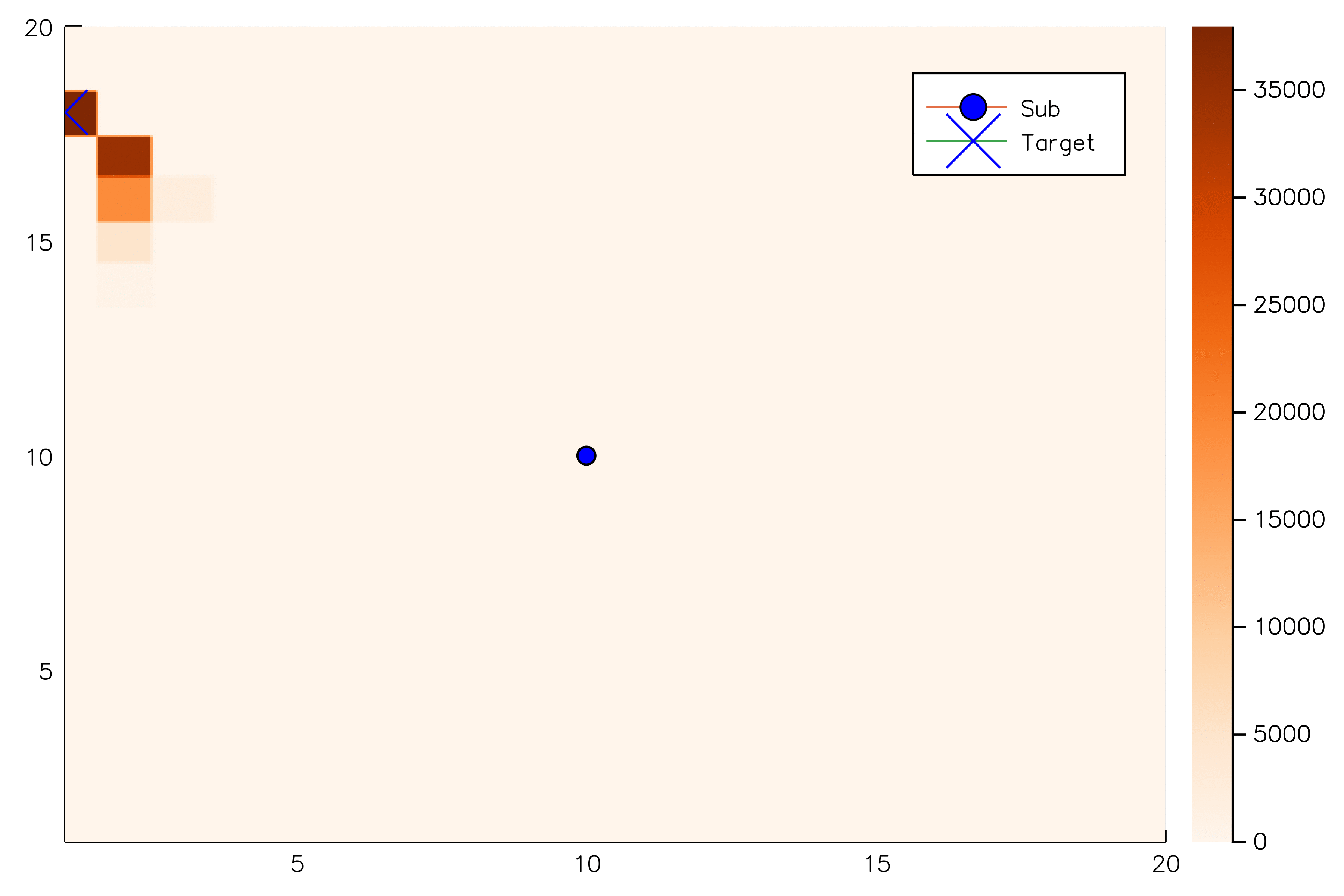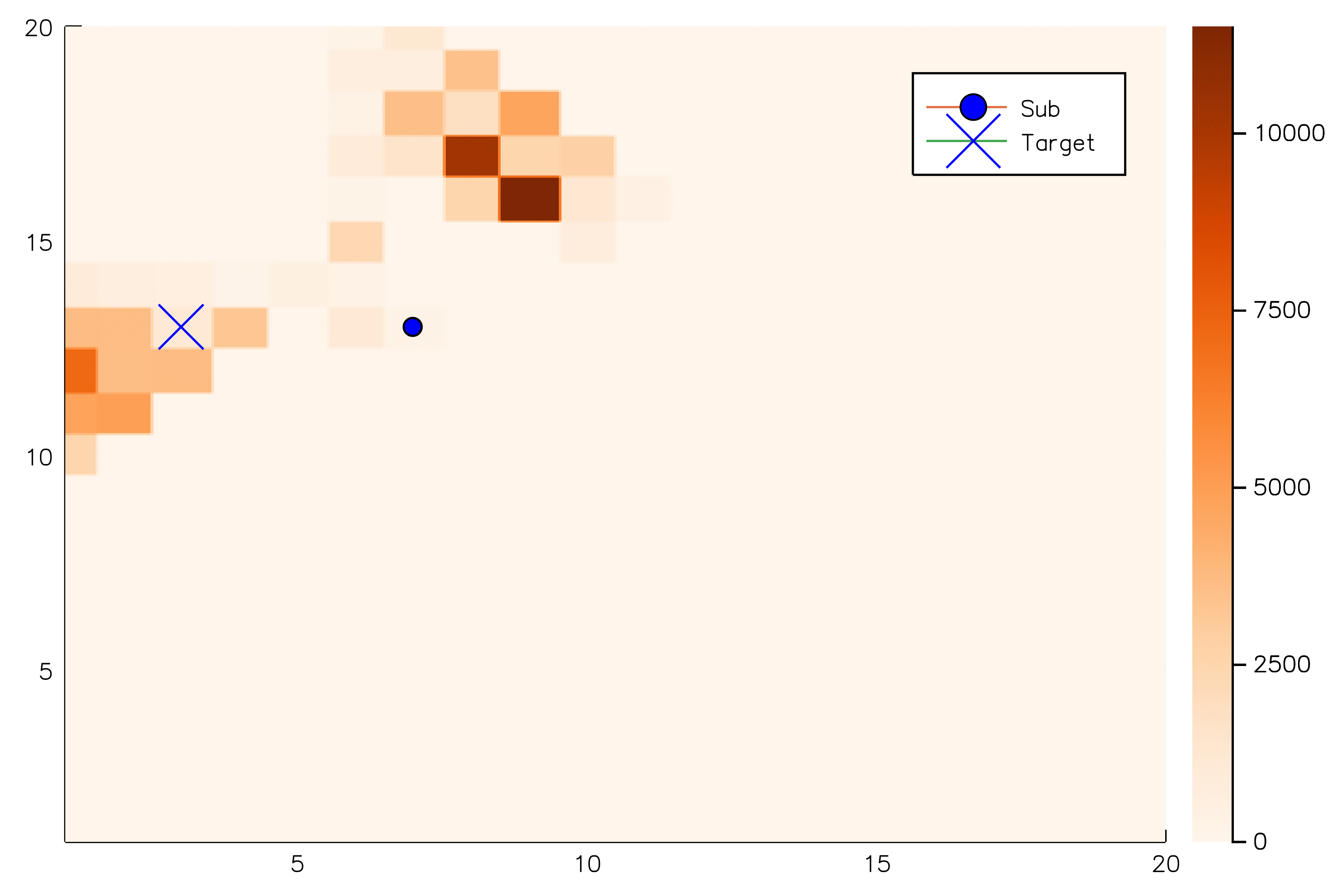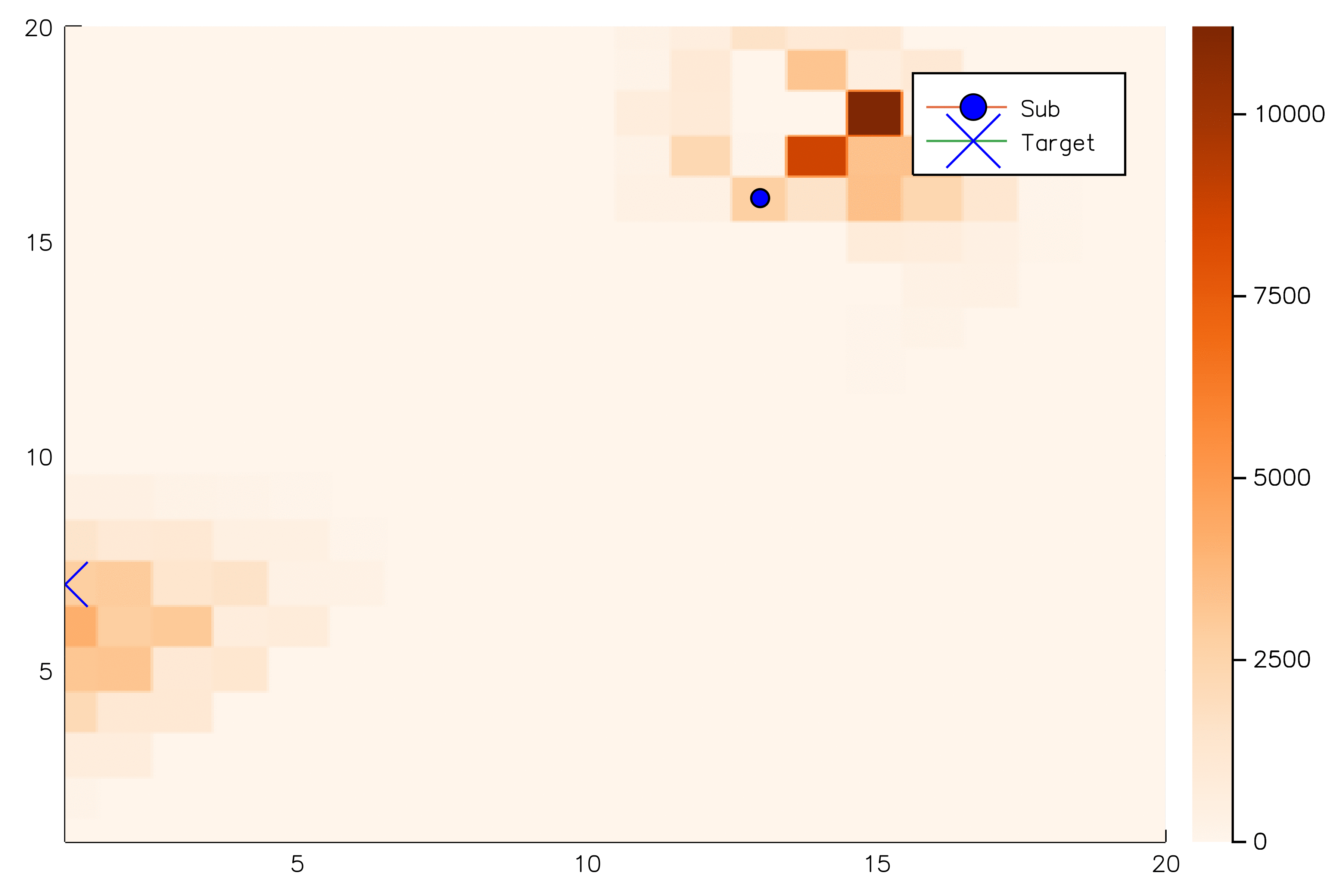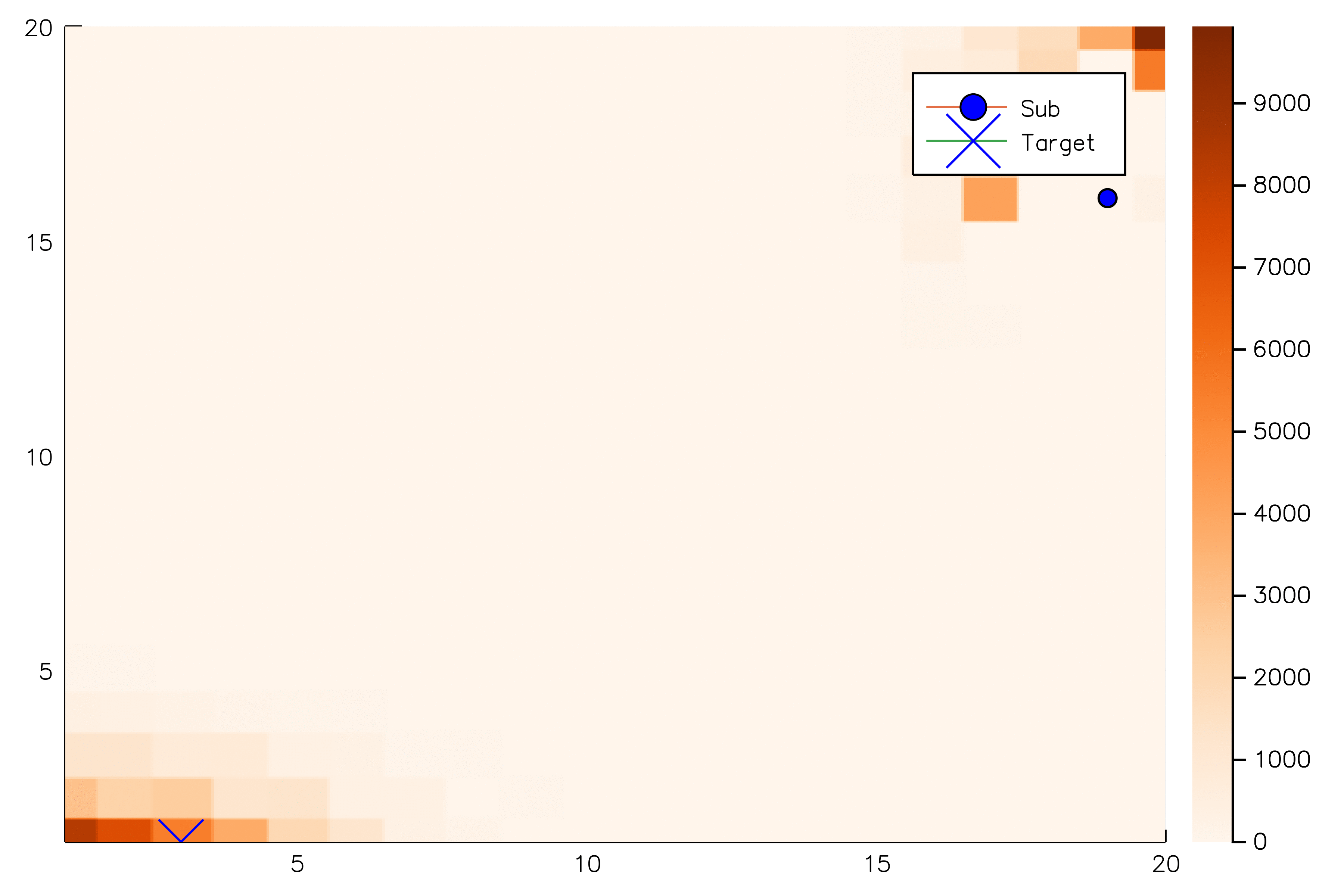
POMDP Example: Laser Tag

POMDP Sense-Plan-Act Loop

Environment

Belief Updater

Policy

\(o\)

\(b\)

\(a\)

\[b_t(s) = P\left(s_t = s \mid a_1, o_1 \ldots a_{t-1}, o_{t-1}\right)\]

Laser Tag POMDP

Online Decision Process Tree Approaches

State Node

Action Node

(Estimate \(Q(s,a)\) here)

MART-POMDP-Intro

By Zachary Sunberg

MART-POMDP-Intro

  • 357

More from Zachary Sunberg