
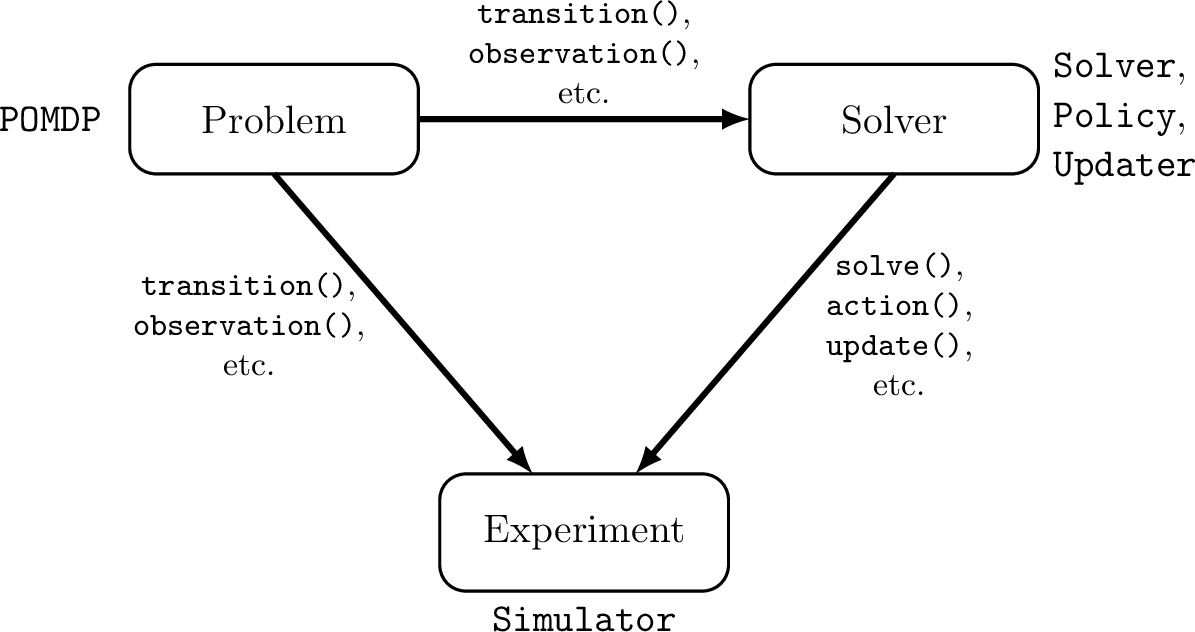
Safe and efficient autonomy in the face of uncertainty
Professor Zachary Sunberg
University of Colorado Boulder
Fall 2022
Background








Mission: deploy autonomy with confidence


Waymo Image By Dllu - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=64517567



Two Objectives for Autonomy
EFFICIENCY
SAFETY
Minimize resource use
(especially time)
Minimize the risk of harm to oneself and others

Safety often opposes Efficiency

Tweet by Nitin Gupta
29 April 2018
https://twitter.com/nitguptaa/status/990683818825736192
Safety, Efficiency, and Uncertainty: A Story

Safety, Efficiency, and Uncertainty: A Story


Why?
Only one safety procedure: Don't approach the vehicle for 10 minutes after a crash (in case it explodes)
Efficiency: Fly planes
Safety: Avoid fires
Solution: gather information (reduce uncertainty) about potentially unsafe situations
Optimization
Safety
Better Performance
Model \(M_2\), Algorithm \(A_2\)
Model \(M_1\), Algorithm \(A_1\)
Efficiency
$$\underset{\pi}{\mathop{\text{maximize}}} \, V^\pi = V^\pi_\text{E} + \lambda V^\pi_\text{S}$$
Safety
Weight
Efficiency
Types of Uncertainty
Alleatory
Epistemic (Static)
Epistemic (Dynamic)


Interaction

MDP

RL
POMDP
Game
Markov Decision Process (MDP)
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distributions
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward function

Alleatory
Reinforcement Learning

Alleatory
Epistemic (Static)
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distributions
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward function
Partially Observable Markov Decision Process (POMDP)

Alleatory
Epistemic (Static)
Epistemic (Dynamic)
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, a)\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R(s, a)\) - Reward function
- \(\mathcal{O}\) - Observation space
- \(Z(o \mid a, s')\) - Observation probability distribution
Partially Observable Markov Game
Alleatory
Epistemic (Static)
Epistemic (Dynamic)
Interaction
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, \bm{a})\) - Transition probability distribution
- \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
- \(R^i(s, \bm{a})\) - Reward function
- \(\mathcal{O}^i, \, i \in 1..k\) - Observation space
- \(Z(o^i \mid \bm{a}, s')\) - Observation probability distribution


POMDPs in Aerospace




1) ACAS
2) Orbital Object Tracking
4) Asteroid Navigation
3) Dual Control
ACAS X
Trusted UAV
Collision Avoidance
[Sunberg, 2016]
[Kochenderfer, 2011]
5) Weather Science
POMDPs in Aerospace
\(\mathcal{S}\): Information space for all objects
\(\mathcal{A}\): Which objects to measure
\(R\): - Entropy
Approximately 20,000 objects >10cm in orbit
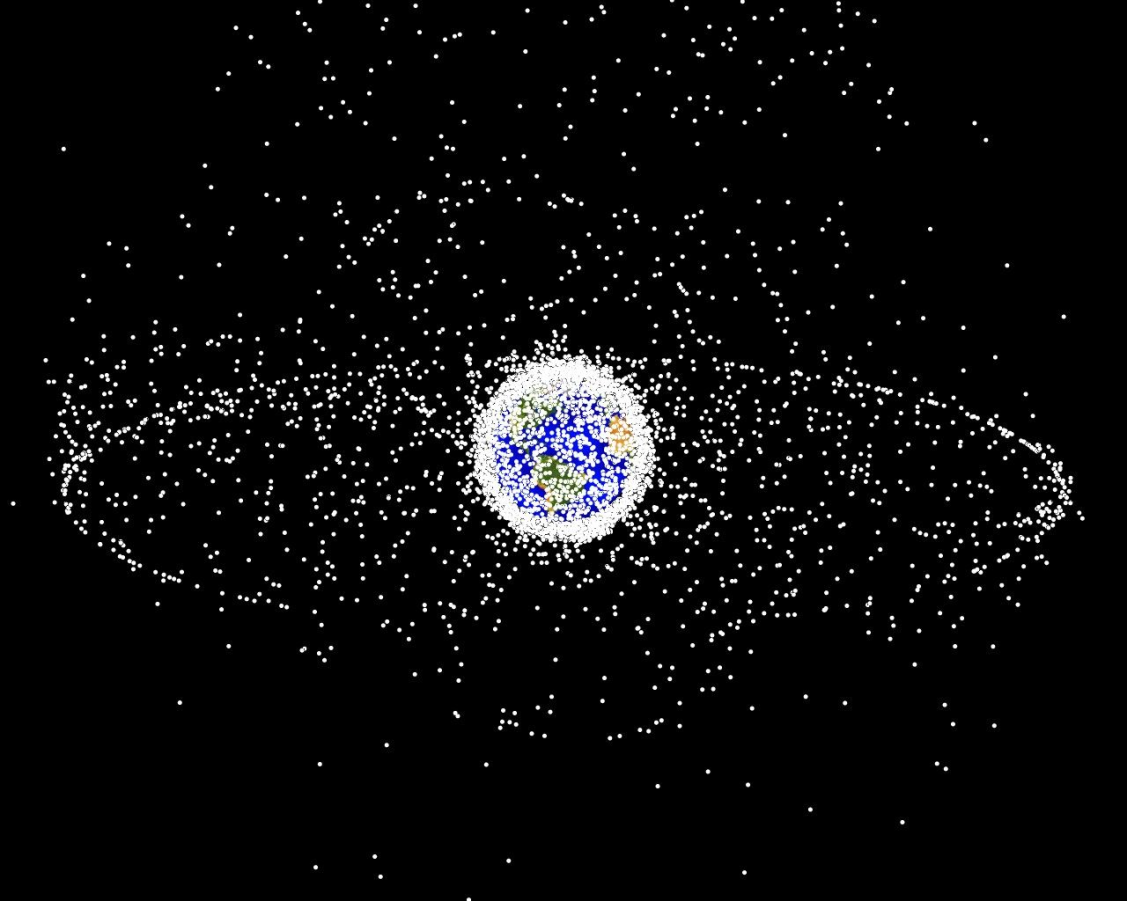
[Sunberg, 2016]
1) ACAS
2) Orbital Object Tracking
4) Asteroid Navigation
3) Dual Control
5) Weather Science
POMDPs in Aerospace


State \(x\) Parameters \(\theta\)
\(s = (x, \theta)\) \(o = x + v\)
POMDP solution automatically balances exploration and exploitation
[Slade, Sunberg, et al. 2017]
1) ACAS
2) Orbital Object Tracking
4) Asteroid Navigation
3) Dual Control
5) Weather Science
POMDPs in Aerospace
Dynamics: Complex gravity field, regolith
State: Vehicle state, local landscape
Sensor: Star tracker?, camera?, accelerometer?
Action: Hopping actuator
[Hockman, 2017]
1) ACAS
2) Orbital Object Tracking
4) Asteroid Navigation
3) Dual Control
5) Weather Science
POMDPs in Aerospace
1) ACAS
2) Orbital Object Tracking
4) Asteroid Navigation
3) Dual Control
5) Weather Science

Solving MDPs - The Value Function
$$V^*(s_t) = \underset{a\in\mathcal{A}}{\max} \left\{R(s_t, a_t) + \gamma E\Big[V^*\left(s_{t+1}\right) \Big]\right\}$$
Involves all future time
Involves only \(t\) and \(t+1\)
$$\underset{\pi:\, \mathcal{S}\to\mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, a_t)\right]$$
$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1})\Big]$$
Value = expected sum of future rewards
Online Tree Search in MDPs

Time
Estimate \(Q(s, a)\) based on children

Challenge: Curse of dimensionality

MDP
POMDP
Inc. Info. Game

Curse of Dimensionality
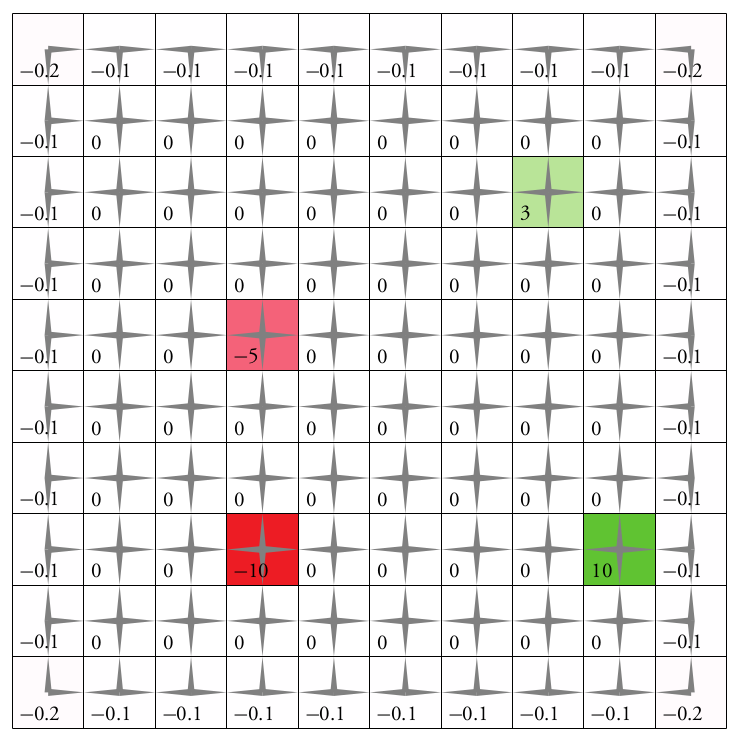
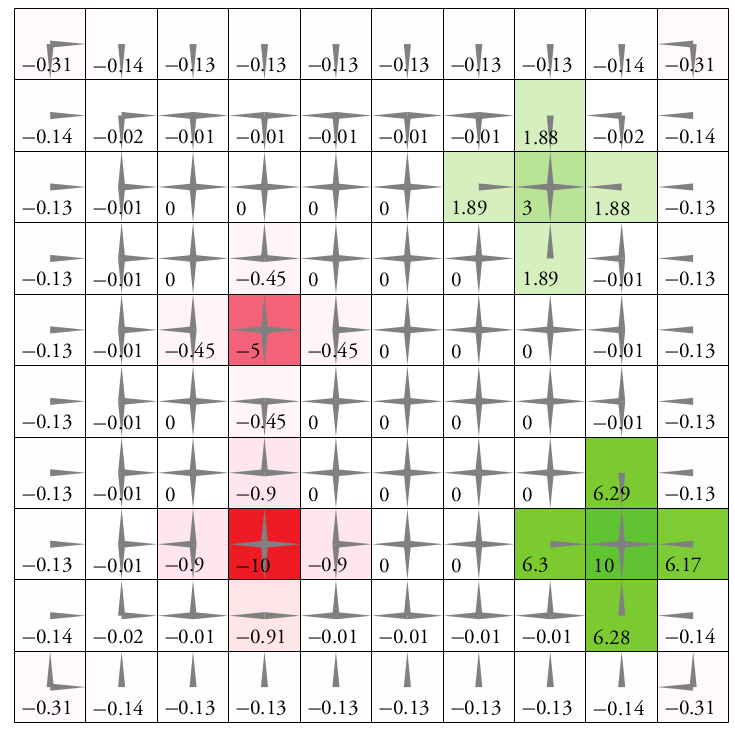
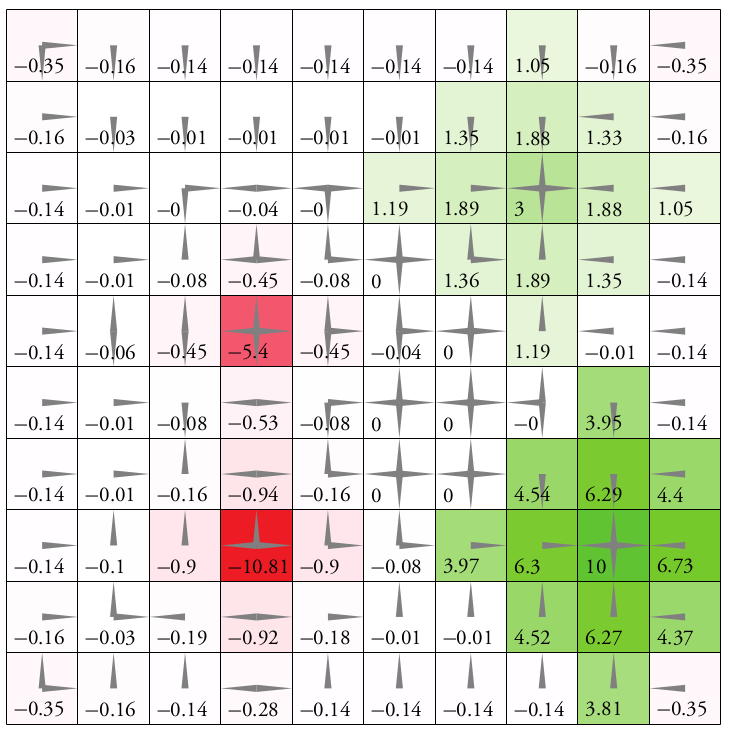
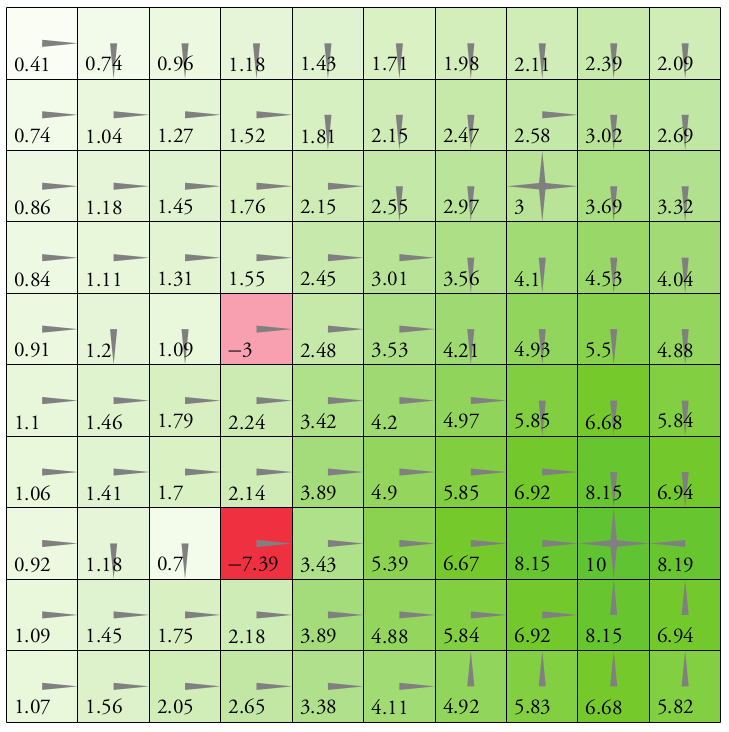

Immediate Reward: \(R(s, a)\)
Value Function: \[Q(s, a) = \text{E}\left[\sum_{t=0}^\infty R(s_t, a_t)\right]\]
\(d\) dimensions, \(k\) segments \(\,\rightarrow \, |S| = k^d\)
Curse of Dimensionality
\(d\) dimensions, \(k\) segments \(\,\rightarrow \, |\mathcal{S}| = k^d\)



1 dimension, 5 segments
\(|\mathcal{S}| = 5\)
2 dimensions, 5 segments
\(|\mathcal{S}| = 25\)
3 dimensions, 5 segments
\(|\mathcal{S}| = 125\)
Challenge: Curse of dimensionality
Adopted Solution: Online sparse tree search

MDP
POMDP
Inc. Info. Game


Online Tree Search in MDPs

Time
Estimate \(Q(s, a)\) based on children

Sparse Sampling
Expand for all actions (\(\left|\mathcal{A}\right| = 2\) in this case)
...
Expand for all \(\left|\mathcal{S}\right|\) states
\(C=3\) states
Sparse Sampling
...
[Kearns, Mansour, & Ng, 2002]
1. Near-optimal policy: \(\left|V^\text{SS}(s) - V^*(s) \right|\leq \epsilon\)
2. Running time independent of state space size:
\(O \left( ( \left|\mathcal{A} \right|C )^H \right) \)
Challenge: Curse of dimensionality
Adopted Solution: Online sparse tree search
Shortcoming: No active information gathering
Additional Challenge: Curse of history

MDP
POMDP
Inc. Info. Game



State
Timestep
Accurate Observations
Goal: \(a=0\) at \(s=0\)
Optimal Policy
Localize
\(a=0\)
POMDP Example: Light-Dark

Autonomous Driving POMDP
POMDP Sense-Plan-Act Loop
Environment
Belief Updater
Policy/Planner
\(b\)
\(a\)
\[b_t(s) = P\left(s_t = s \mid a_1, o_1 \ldots a_{t-1}, o_{t-1}\right)\]
True State
Observation



A POMDP is an MDP on the Belief Space
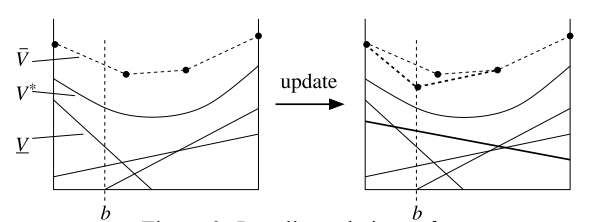
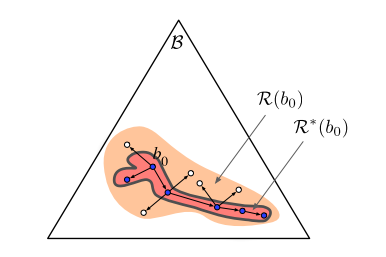
SARSOP can solve some POMDPs with thousands of states offline
but
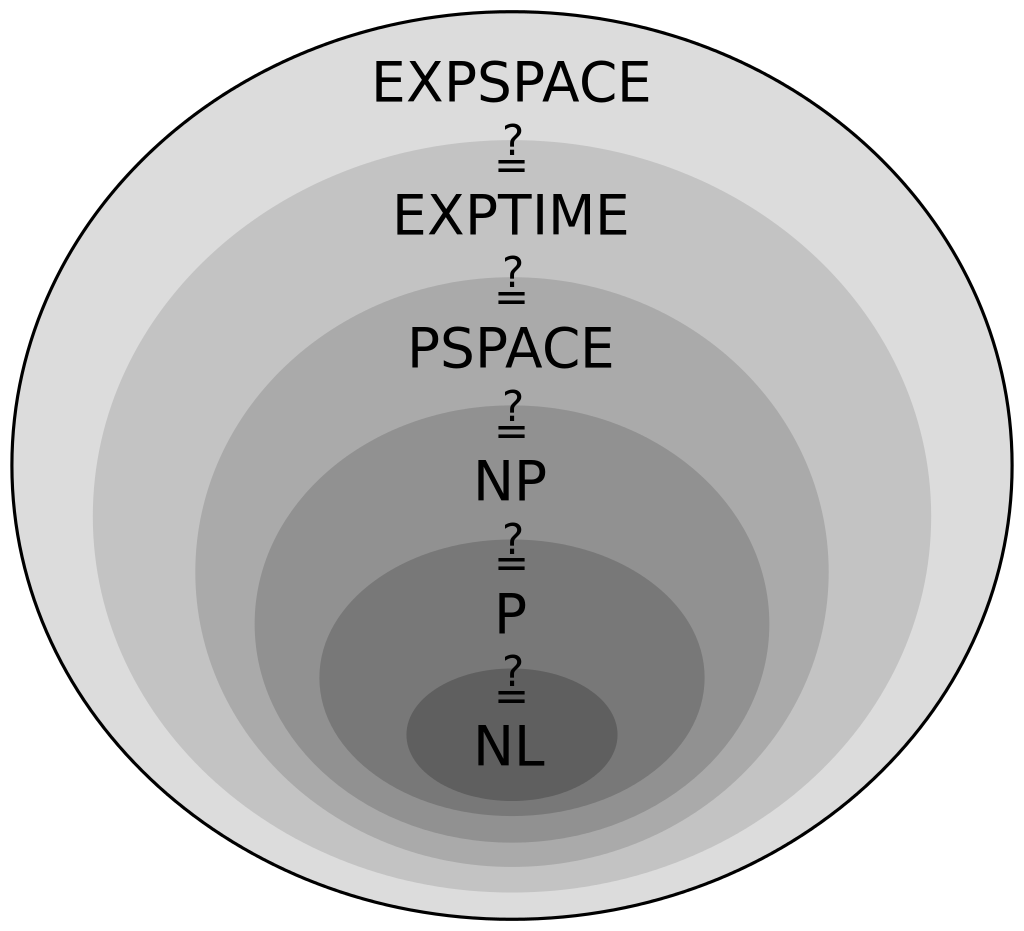
The POMDP is PSPACE-Complete
Intractable!
- A POMDP is an MDP on the Belief Space but belief updates are expensive
- POMCP* uses simulations of histories instead of full belief updates
- Each belief is implicitly represented by a collection of unweighted particles


[Ross, 2008] [Silver, 2010]
*(Partially Observable Monte Carlo Planning)
REVISE SLIDE FOR FUTURE
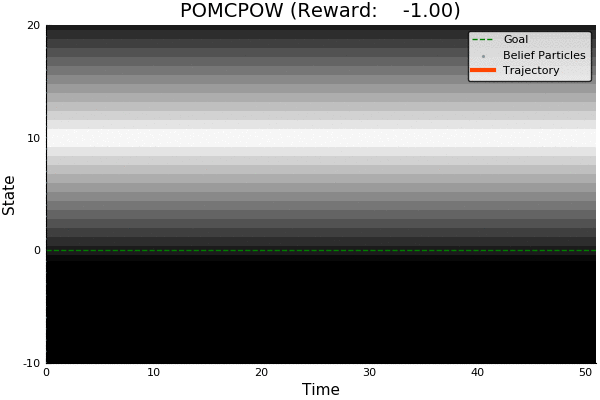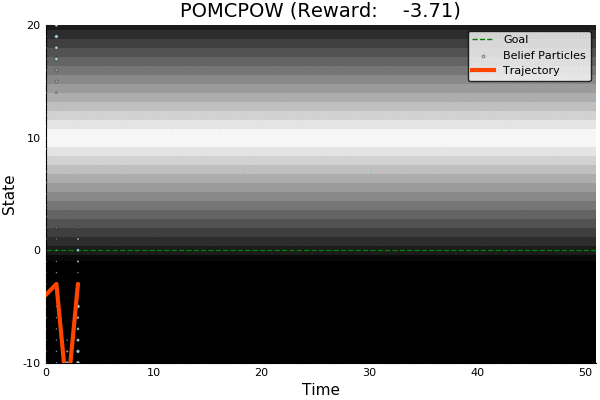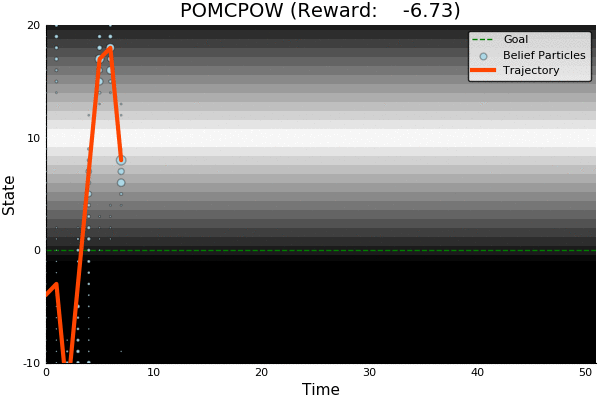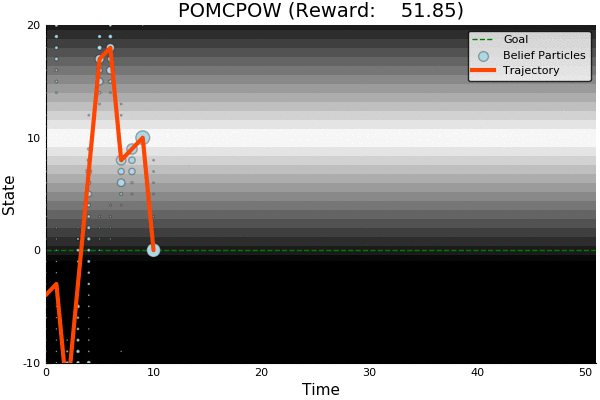



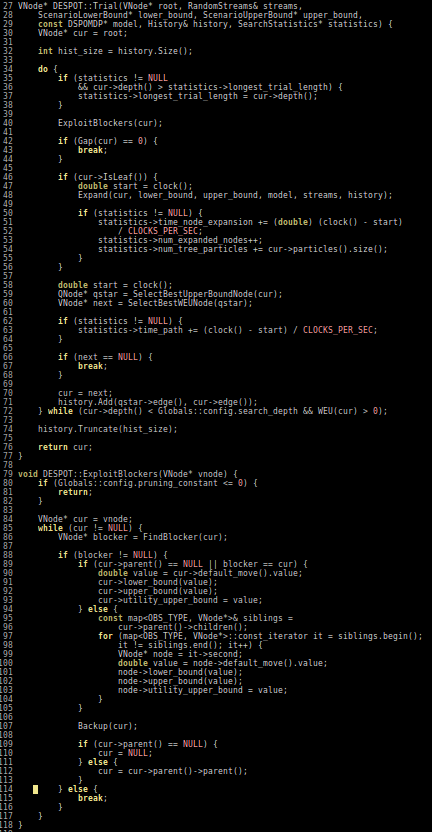
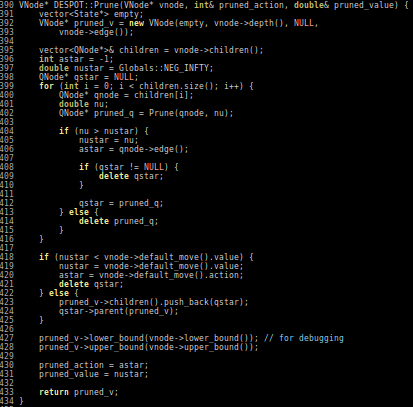
POMCP
POMCP-DPW
POMCPOW
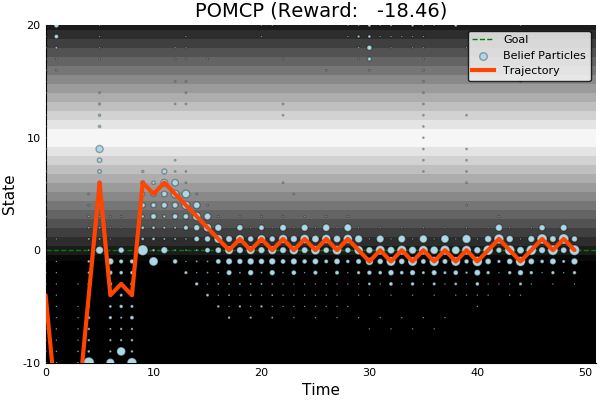
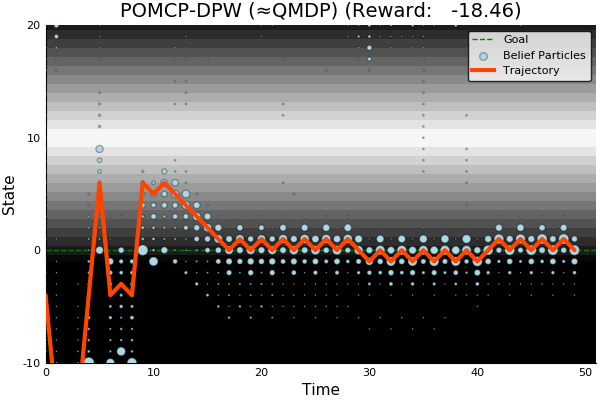
[Sunberg and Kochenderfer, ICAPS 2018]
First scalable algorithm for general POMDPs with continuous \(O\)
REMOVE SLIDE IN FUTURE
Challenge: Curse of dimensionality
Adopted Solution: Online sparse tree search
Shortcoming: No active information gathering
Additional Challenge: Curse of history
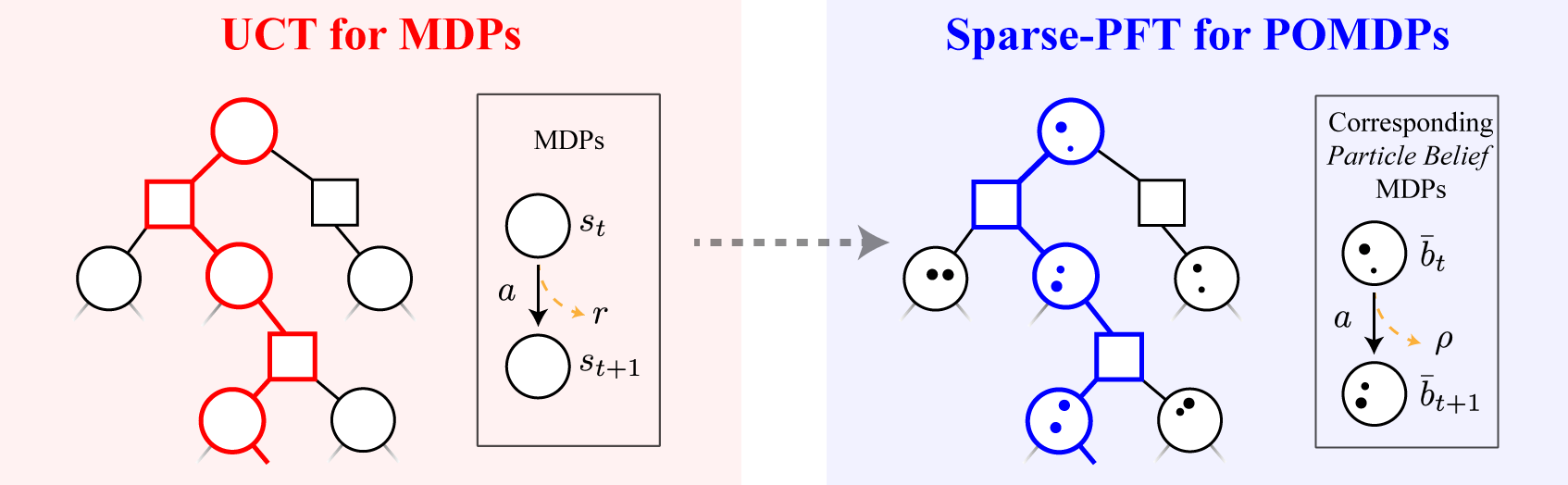
Adopted Solution: Particle filtering

MDP
POMDP
Inc. Info. Game


POMDP = Belief MDP
Efficient POMDP Approximations
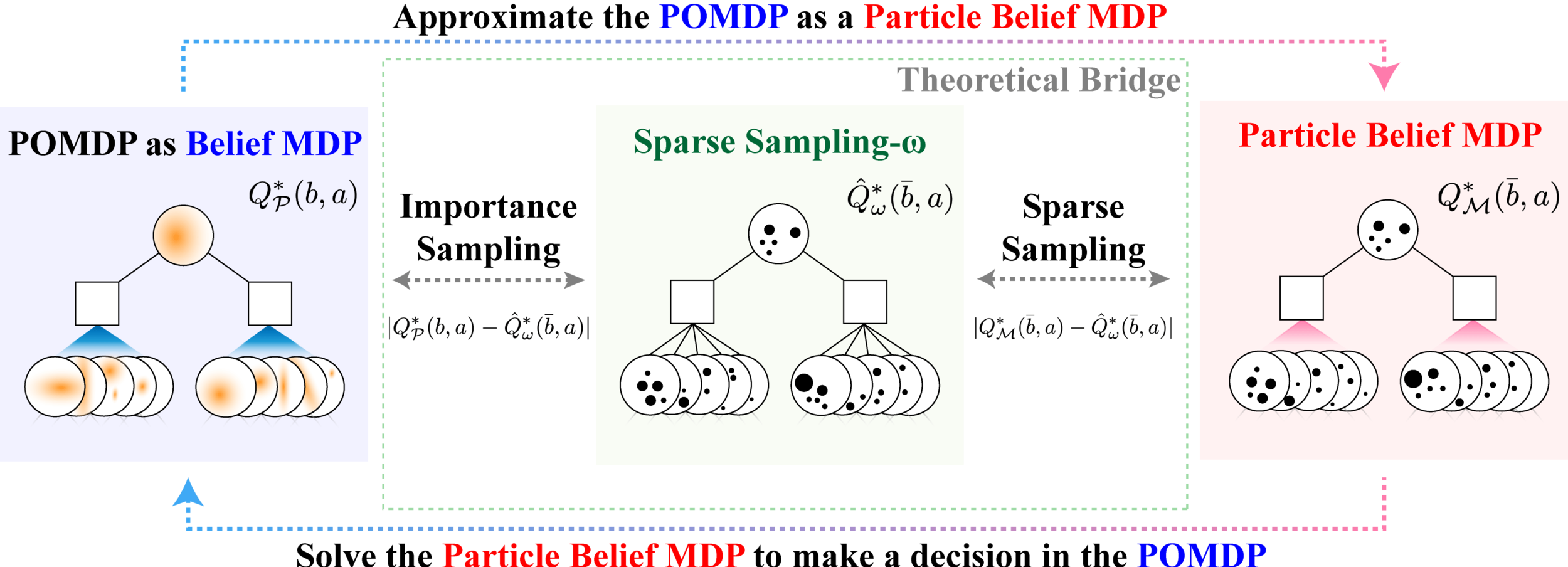
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]
For and \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,
\(\mathbf{M}_\mathbf{P}\) = Particle belief MDP approximation of POMDP \(\mathbf{P}\)
[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, 2022 (?)]
No dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!
Continuous Observation Analytical Results (POWSS)


Our simplified algorithm is near-optimal
[Lim, Tomlin, & Sunberg, IJCAI 2020]
Easy MDP to POMDP Extension






MDP trained on normal drivers



MDP trained on all drivers
Omniscient
POMCPOW (Ours)
Simulation results
[Sunberg & Kochenderfer, T-ITS 2022]

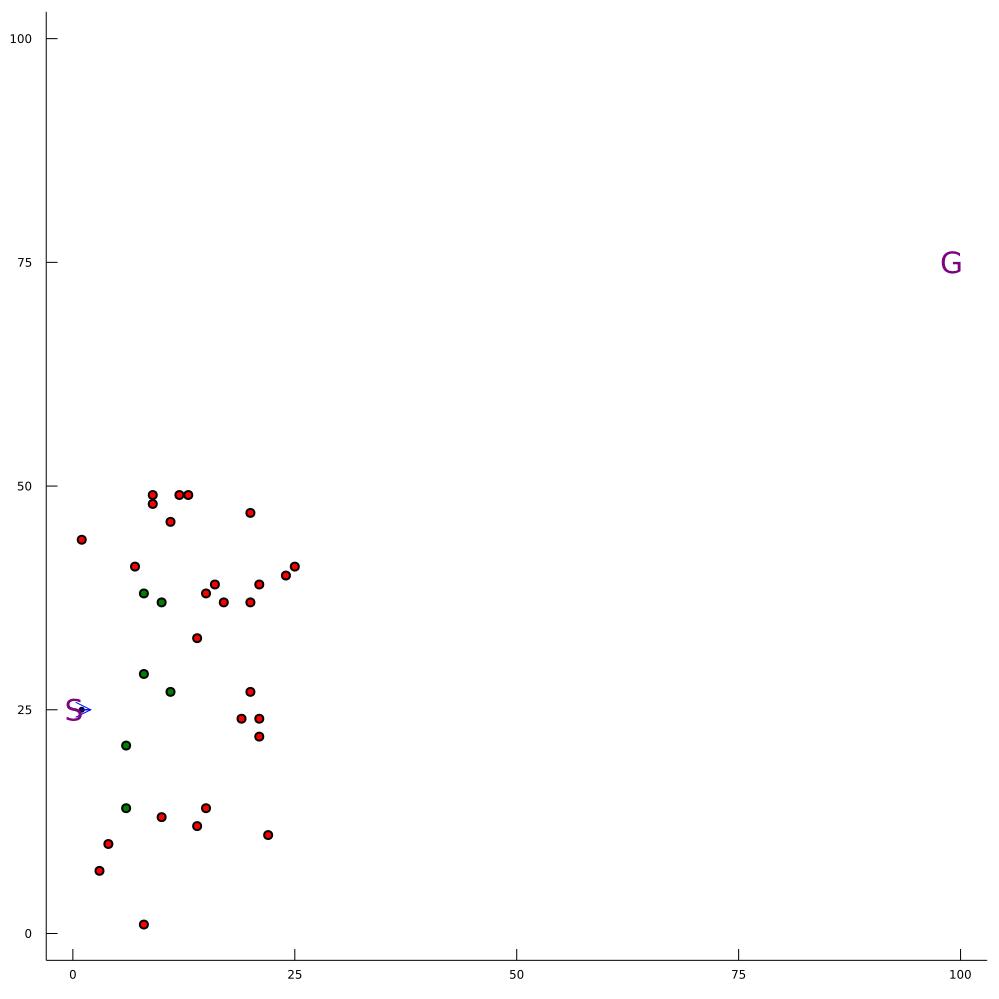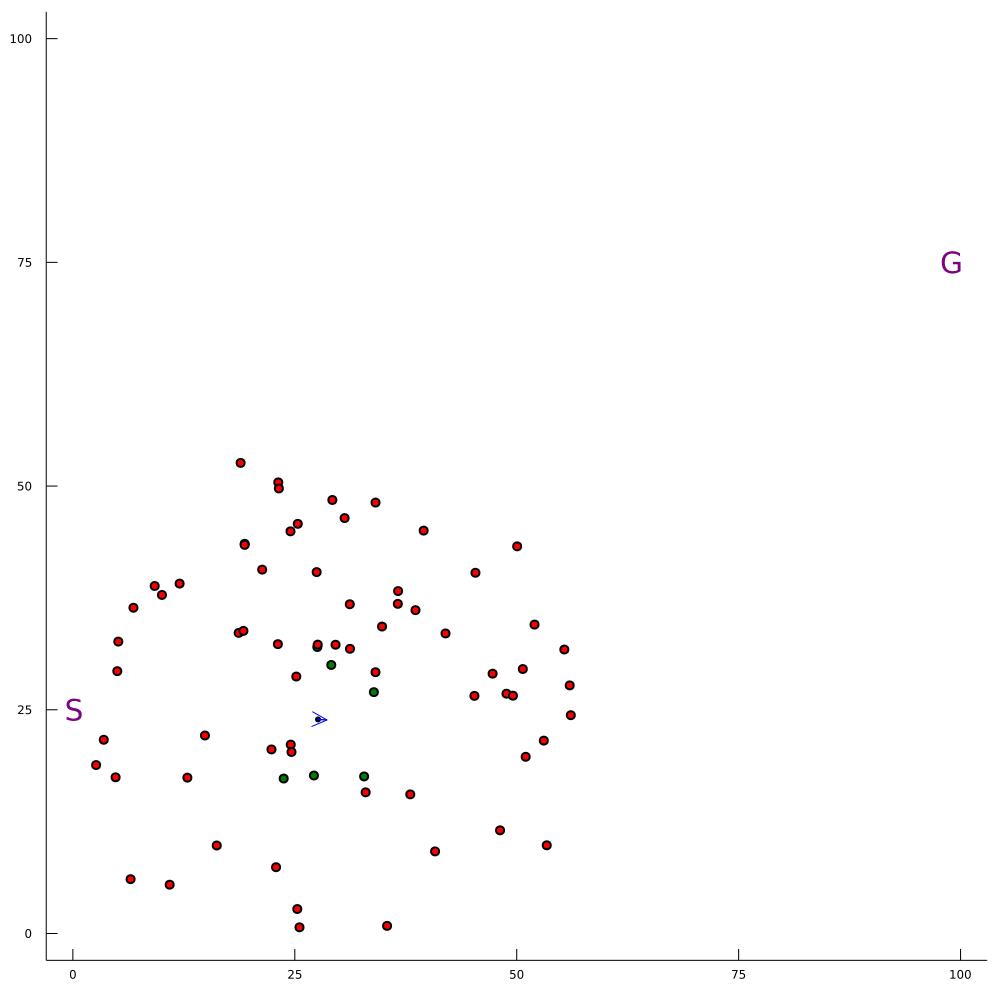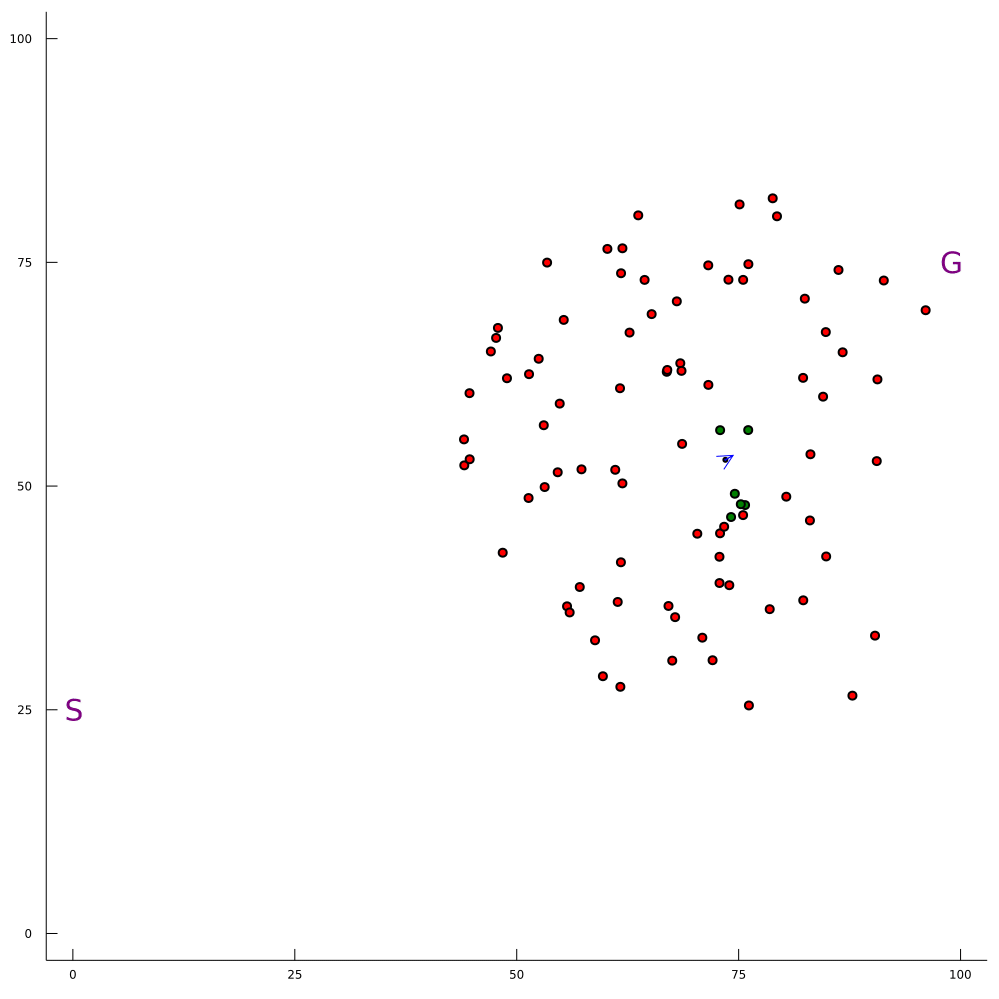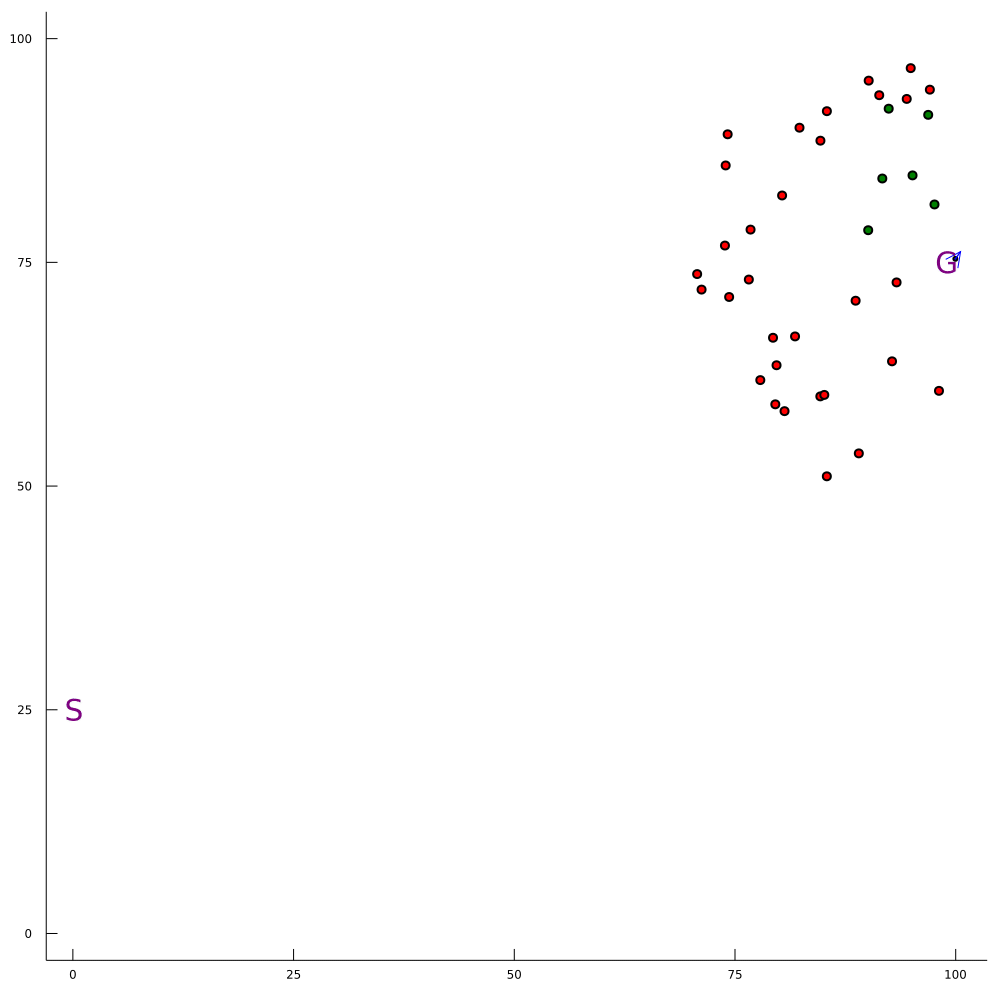
Conventional 1D POMDP
2D POMDP

Pedestrian Navigation

[Gupta, Hayes, & Sunberg, AAAI 2021]
POMDP Planning with Image Observations
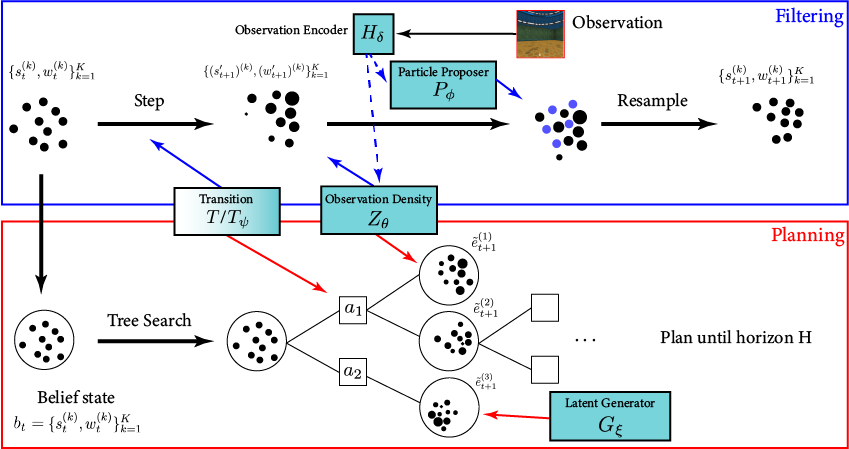
[Deglurkar, Lim, Sunberg, & Tomlin, 2023?]
Additional ADCL (PO)MDP Projects
- Motion planning under uncertainty with temporal logic specifications
- Explainability
- Adaptive Stress Testing
[Ho, Sunberg, and Lahijanian, ICRA 2022, ICRA 2023 (?)]


[Tucker, Wagner, and Sunberg, AMOS 22]
Actions
Observations
States
POMDPs with Continuous...
- PO-UCT (POMCP)
- DESPOT
- POMCPOW
- DESPOT-α
- LABECOP
- Ada-OPS
- GPS-ABT
- BOMCP
- VOMCPOW
BOMCP


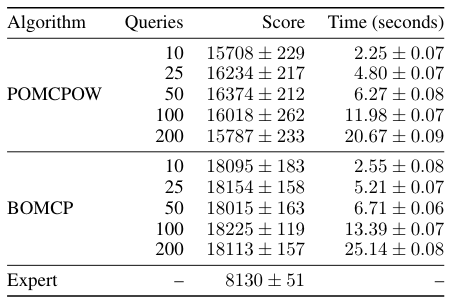
[Mern, Sunberg, et al. AAAI 2021]
Voronoi Progressive Widening
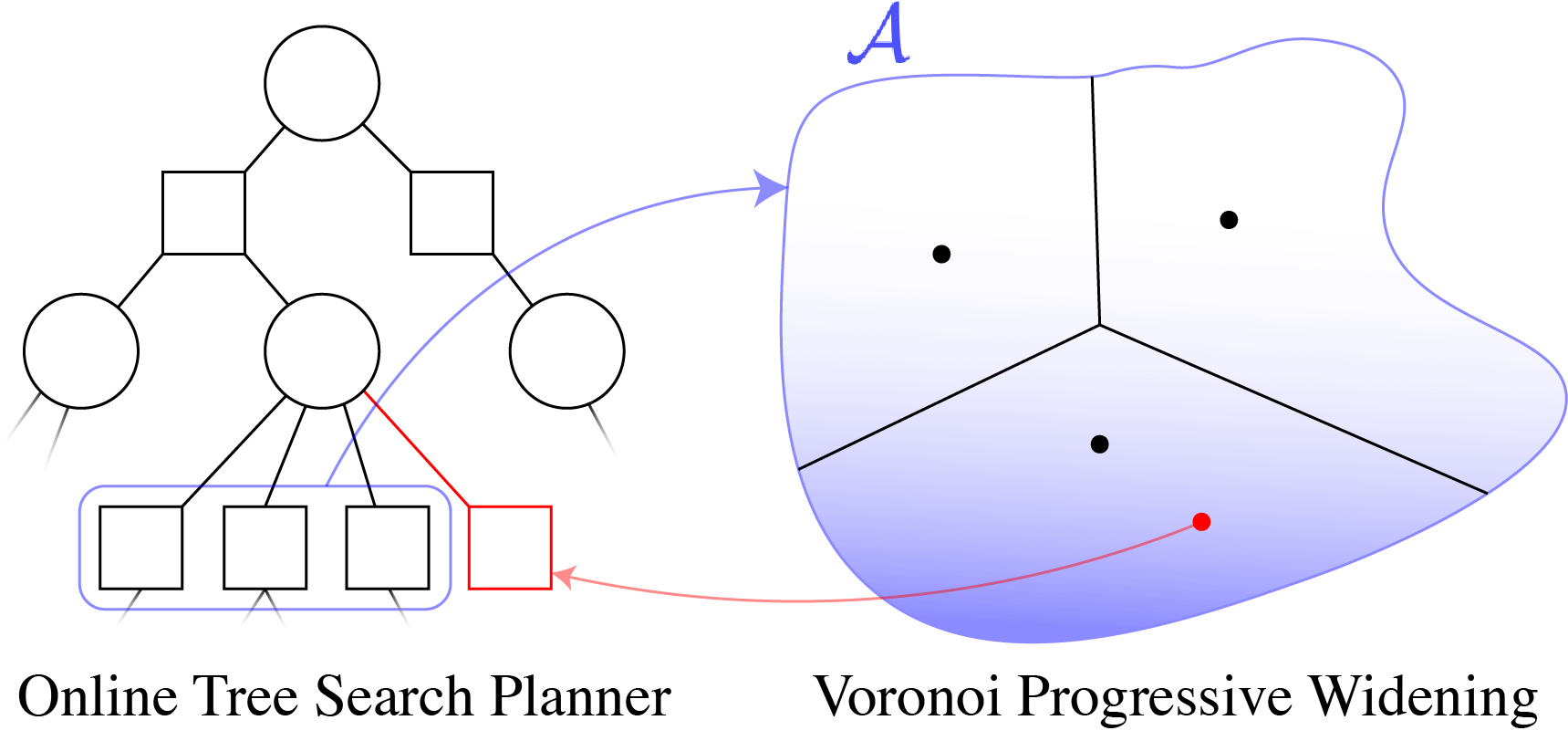
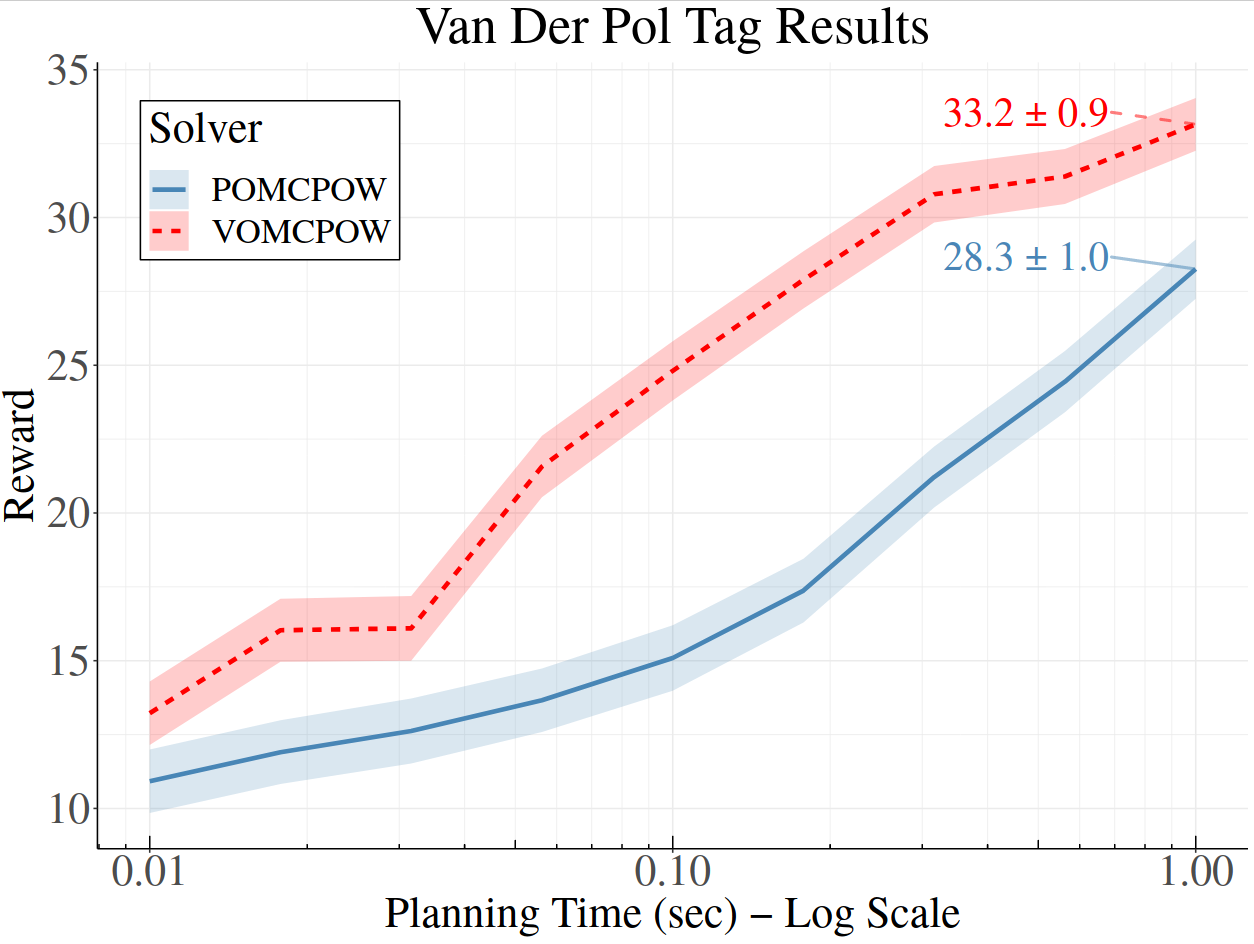

[Lim, Tomlin, & Sunberg CDC 2021]
Motion Planning under Uncertainty with Temporal Logic Specifications
[Ho, Sunberg, and Lahijanian, ICRA 2022, ICRA 2023 (?)]
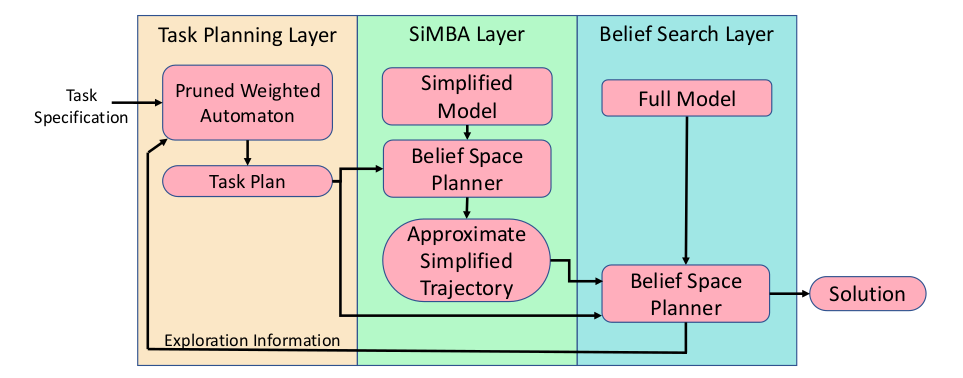
Key Idea: Simplified Model with Belief Approximation (SiMBA)

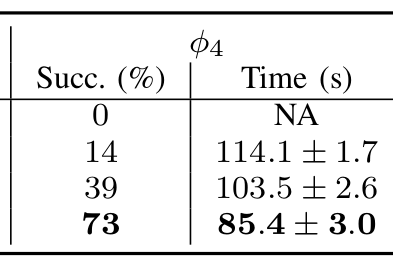

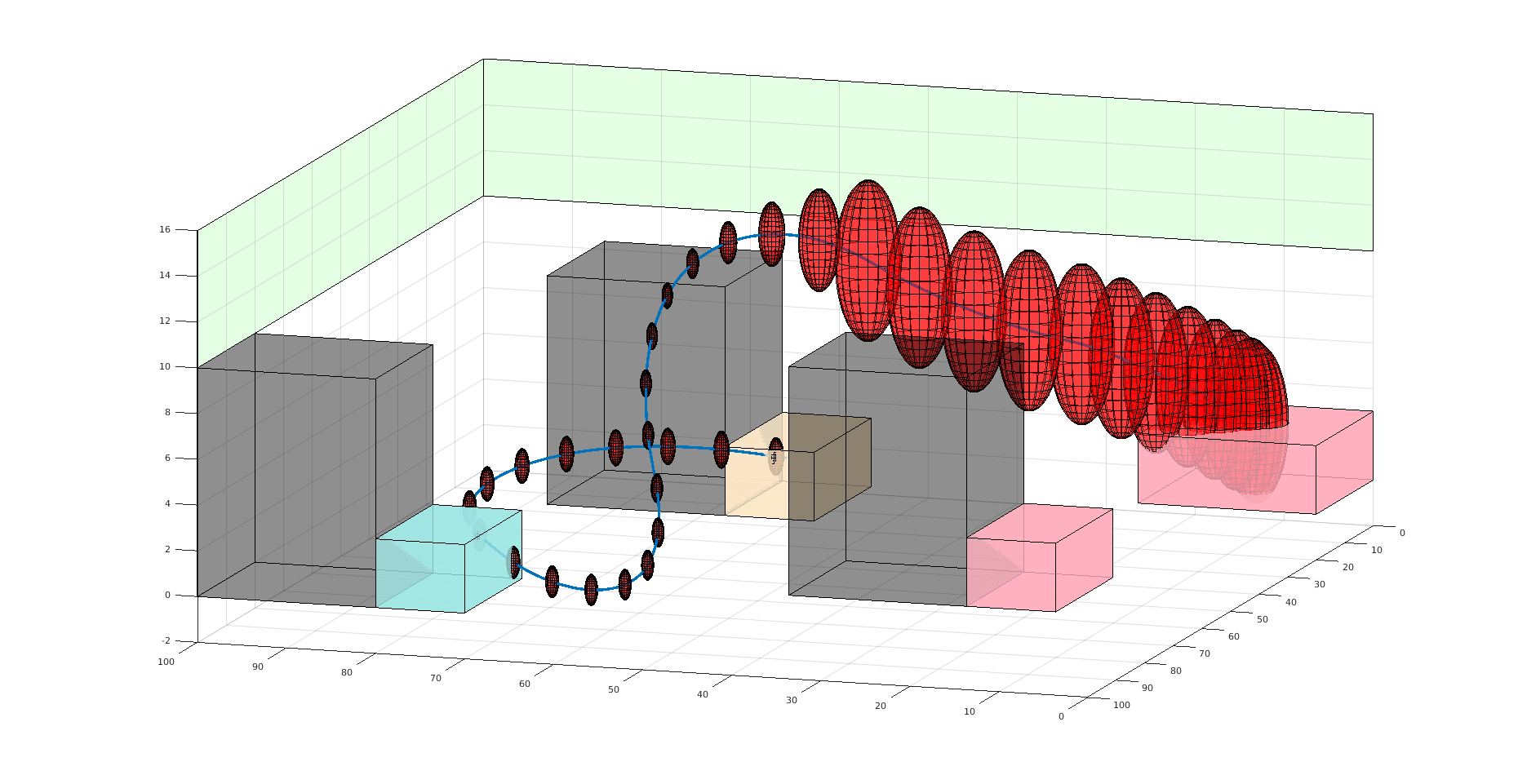
Challenge: Curse of dimensionality
Adopted Solution: Online sparse tree search
Shortcoming: No active information gathering
Additional Challenge: Curse of history
Adopted Solution: Particle filtering
Shortcoming: No mixed strategies

MDP
POMDP
Inc. Info. Game


POMDP = Belief MDP
Interaction Uncertainty

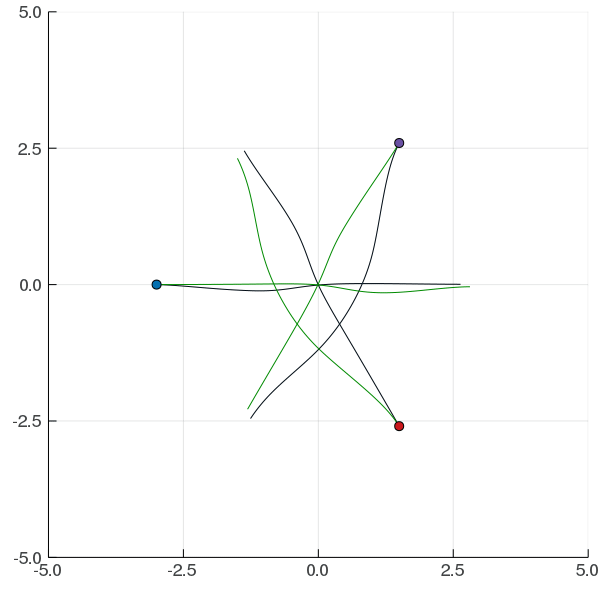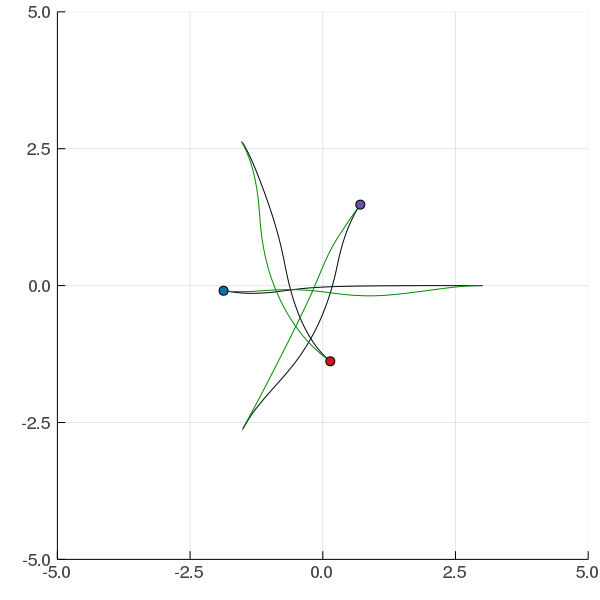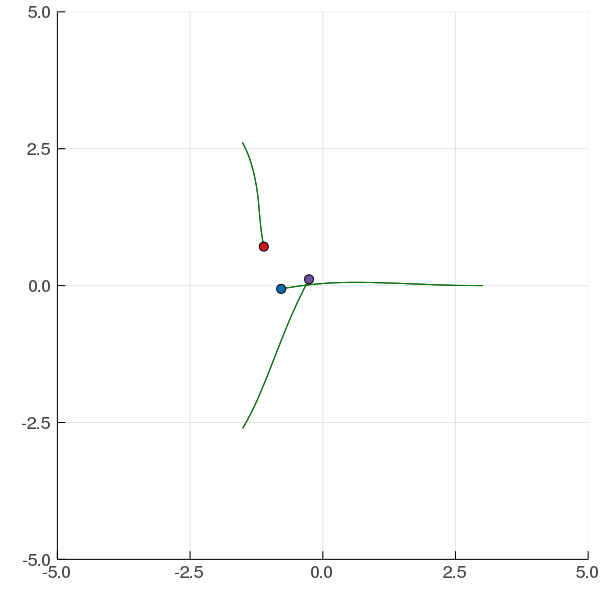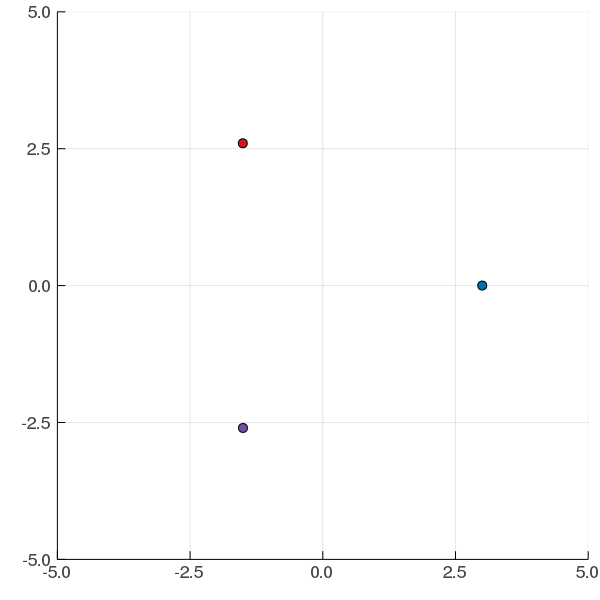
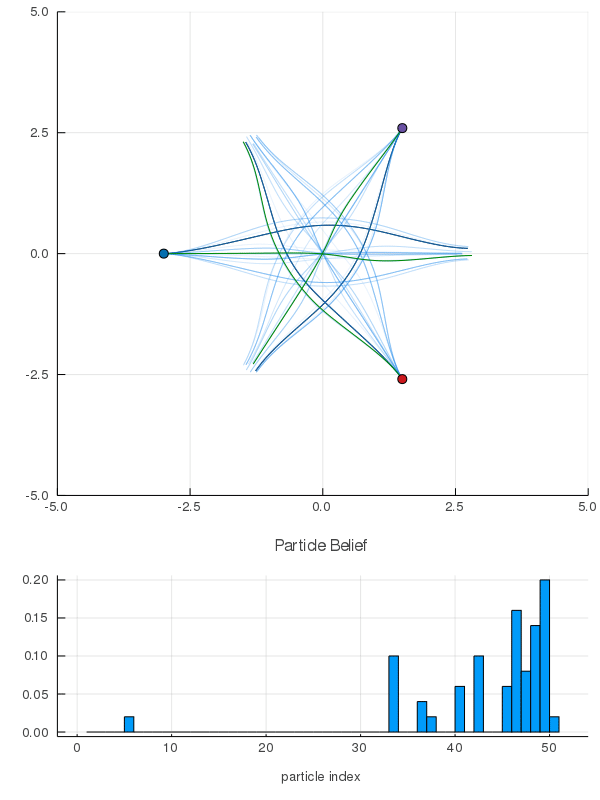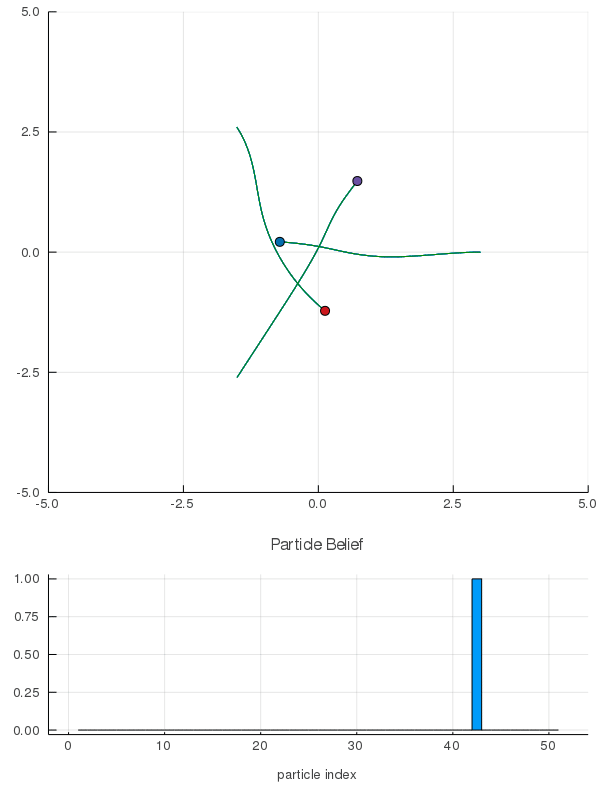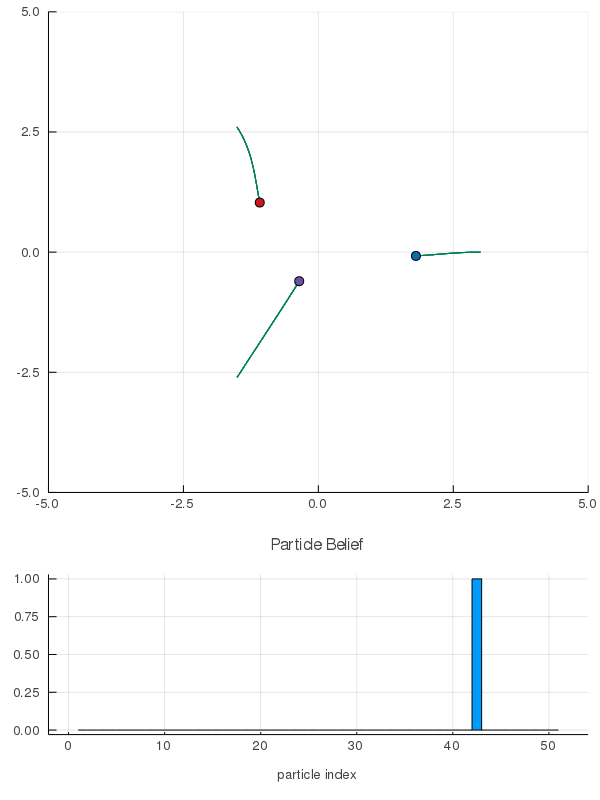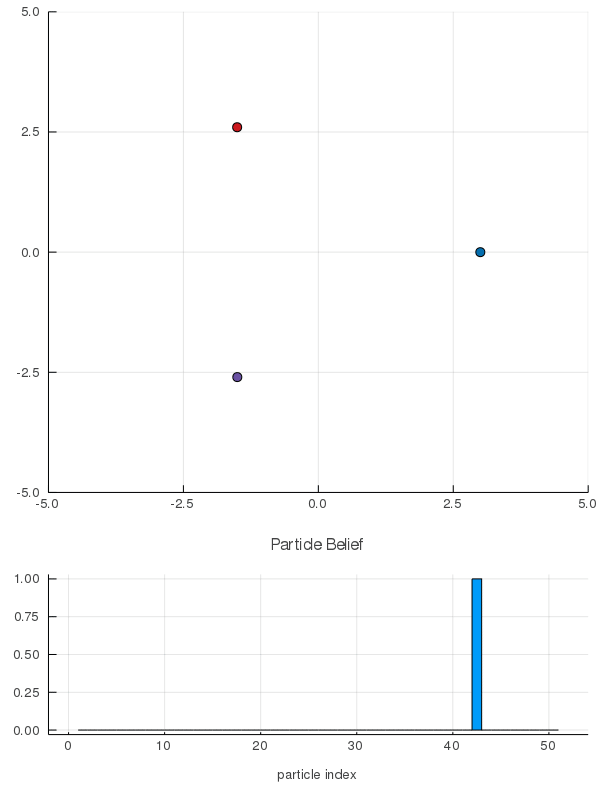

[Peters, Tomlin, and Sunberg 2020]
Game Theory
Nash Equilibrium: All players play a best response.
Optimization Problem
(MDP or POMDP)
\(\text{maximize} \quad f(x)\)
Game
Player 1: \(U_1 (a_1, a_2)\)
Player 2: \(U_2 (a_1, a_2)\)
Collision
Example: Airborne Collision Avoidance
|
|
|
|
|
Player 1
Player 2
Up
Down
Up
Down
-6, -6
-1, 1
1, -1
-4, -4

Collision
Mixed Strategies
Nash Equilibrium \(\iff\) Zero Exploitability
\[\sum_i \max_{\pi_i'} U_i(\pi_i', \pi_{-i})\]
No Pure Nash Equilibrium!
Instead, there is a Mixed Nash where each player plays up or down with 50% probability.
If either player plays up or down more than 50% of the time, their strategy can be exploited.
Exploitability (zero sum):
Strategy (\(\pi_i\)): probability distribution over actions
|
|
|
|
|
Up
Down
Up
Down
-1, 1
1, -1
1, -1
-1, 1
Collision
Collision
Challenge: Curse of dimensionality
Adopted Solution: Online sparse tree search
Shortcoming: No active information gathering
Additional Challenge: Curse of history
Adopted Solution: Particle filtering
Shortcoming: No mixed strategies

MDP
POMDP
Inc. Info. Game


Additional Challenge: Computing Mixed strategies
Solution: ???
POMDP = Belief MDP
Best response = POMDP
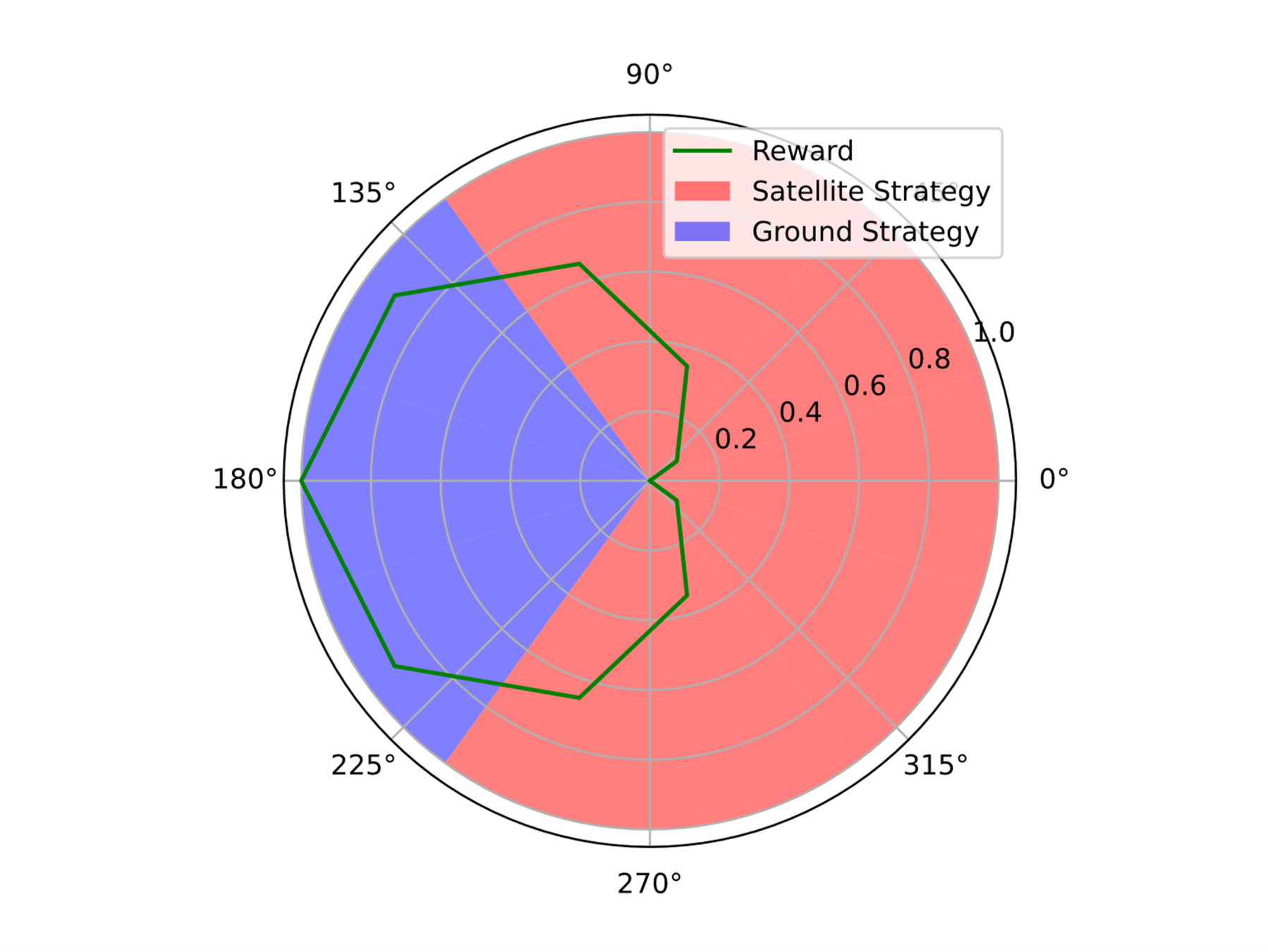
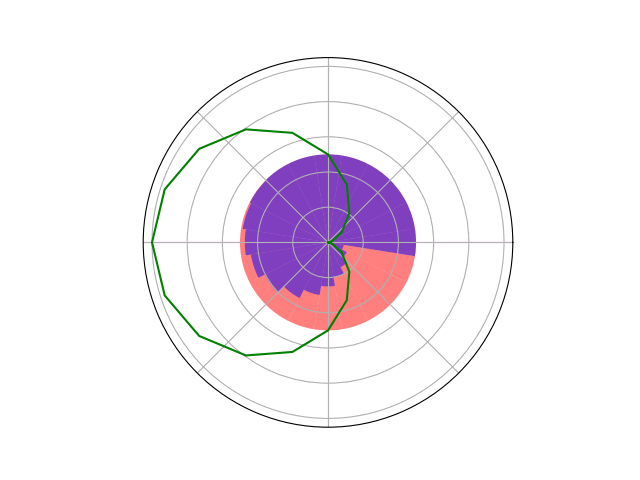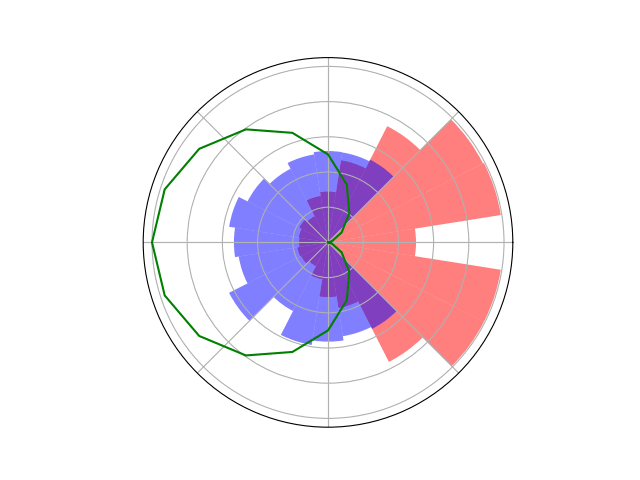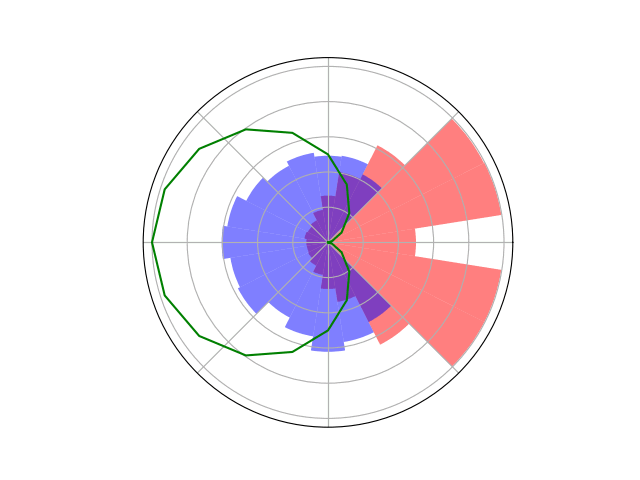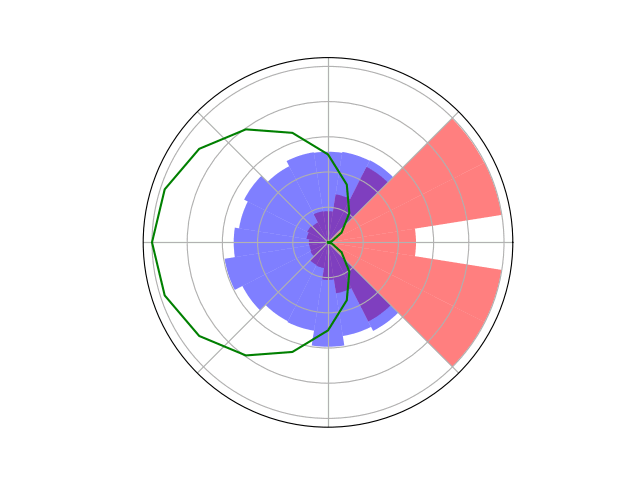
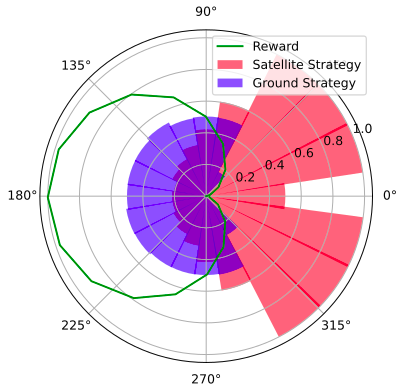
Space Domain Awareness Games
Simplified SDA Game

1
2
...
...
...
...
...
...
...
\(N\)
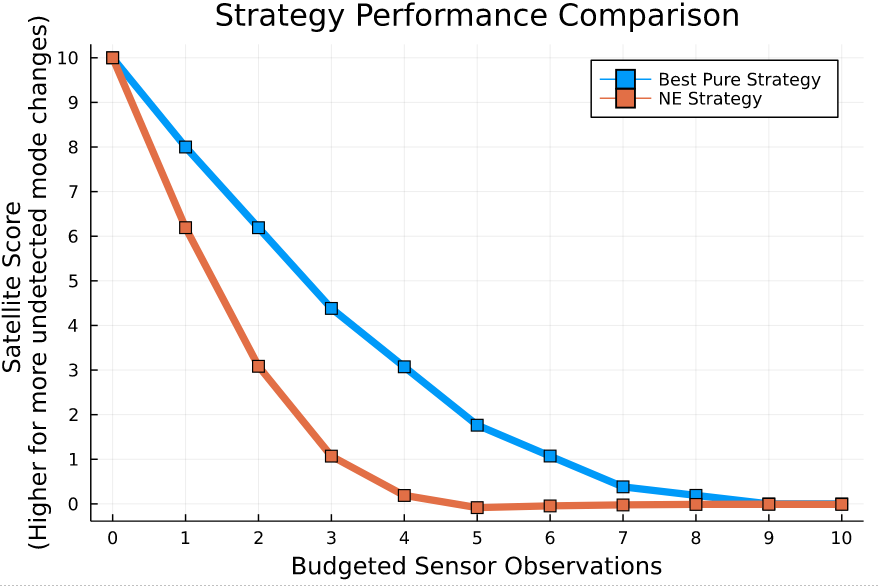
[Becker & Sunberg CDC 2021]
Counterfactual Regret Minimization Training

Open Source Research Software
Challenges for POMDP Software
- There is a huge variety of
- Problems
- Continuous/Discrete
- Fully/Partially Observable
- Generative/Explicit
- Simple/Complex
- Solvers
- Online/Offline
- Alpha Vector/Graph/Tree
- Exact/Approximate
- Domain-specific heuristics
- Problems
- POMDPs are computationally difficult.
Explicit
Black Box
("Generative" in POMDP lit.)

\(s,a\)
\(s', o, r\)
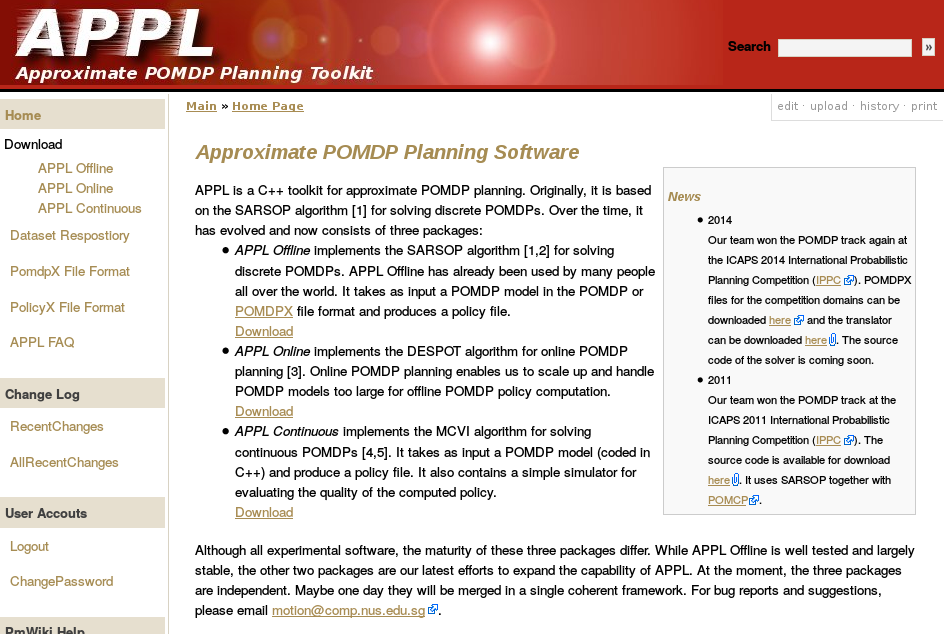
Previous C++ framework: APPL
"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."
Open Source Research Software
- Performant
- Flexible and Composable
- Free and Open
- Easy for a wide range of people to use (for homework)
- Easy for a wide range of people to understand
C++
Python
Python, Matlab
Python, Matlab
C++
C++
Python
Fast
Easy
2013

We love [Matlab, Lisp, Python, Ruby, Perl, Mathematica, and C]; they are wonderful and powerful. For the work we do — scientific computing, machine learning, data mining, large-scale linear algebra, distributed and parallel computing — each one is perfect for some aspects of the work and terrible for others. Each one is a trade-off.
We are greedy: we want more.
2012
Julia - Speed
Celeste Project
1.54 Petaflops


POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

Mountain Car
partially_observable_mountaincar = QuickPOMDP(
actions = [-1., 0., 1.],
obstype = Float64,
discount = 0.95,
initialstate = ImplicitDistribution(rng -> (-0.2*rand(rng), 0.0)),
isterminal = s -> s[1] > 0.5,
gen = function (s, a, rng)
x, v = s
vp = clamp(v + a*0.001 + cos(3*x)*-0.0025, -0.07, 0.07)
xp = x + vp
if xp > 0.5
r = 100.0
else
r = -1.0
end
return (sp=(xp, vp), r=r)
end,
observation = (a, sp) -> Normal(sp[1], 0.15)
)using POMDPs
using QuickPOMDPs
using POMDPPolicies
using Compose
import Cairo
using POMDPGifs
import POMDPModelTools: Deterministic
mountaincar = QuickMDP(
function (s, a, rng)
x, v = s
vp = clamp(v + a*0.001 + cos(3*x)*-0.0025, -0.07, 0.07)
xp = x + vp
if xp > 0.5
r = 100.0
else
r = -1.0
end
return (sp=(xp, vp), r=r)
end,
actions = [-1., 0., 1.],
initialstate = Deterministic((-0.5, 0.0)),
discount = 0.95,
isterminal = s -> s[1] > 0.5,
render = function (step)
cx = step.s[1]
cy = 0.45*sin(3*cx)+0.5
car = (context(), circle(cx, cy+0.035, 0.035), fill("blue"))
track = (context(), line([(x, 0.45*sin(3*x)+0.5) for x in -1.2:0.01:0.6]), stroke("black"))
goal = (context(), star(0.5, 1.0, -0.035, 5), fill("gold"), stroke("black"))
bg = (context(), rectangle(), fill("white"))
ctx = context(0.7, 0.05, 0.6, 0.9, mirror=Mirror(0, 0, 0.5))
return compose(context(), (ctx, car, track, goal), bg)
end
)
energize = FunctionPolicy(s->s[2] < 0.0 ? -1.0 : 1.0)
makegif(mountaincar, energize; filename="out.gif", fps=20)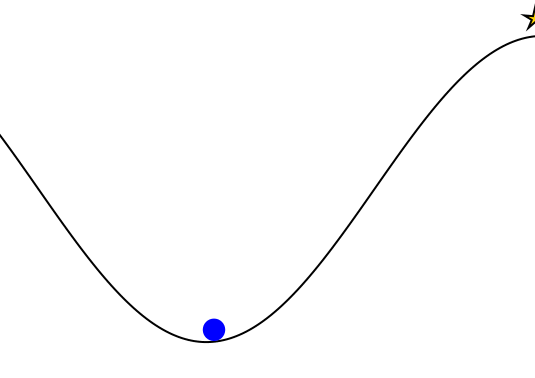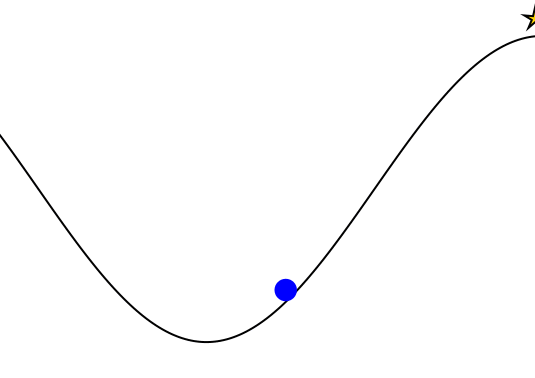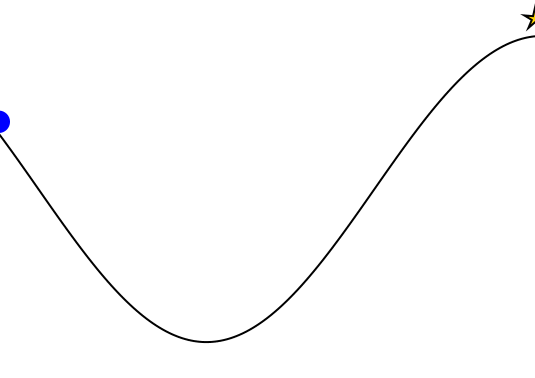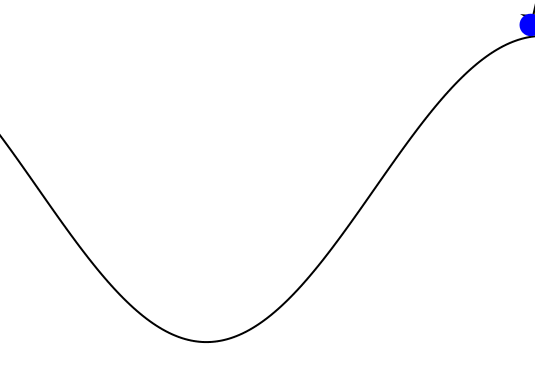




Members








- Astrodynamics
- Autonomous Systems (me)
- Bioastronautics
- Fluids, Structures and Materials
- Remote Sensing
-
Application Deadlines
Spring 2023: October 1
Fall 2023: December 1 -
Applicant Mentoring program
Thank You!

Recent and Current Projects
Human Behavior Model: IDM and MOBIL

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).
A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).
A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).





All drivers normal




Omniscient
Mean MPC
QMDP
POMCPOW
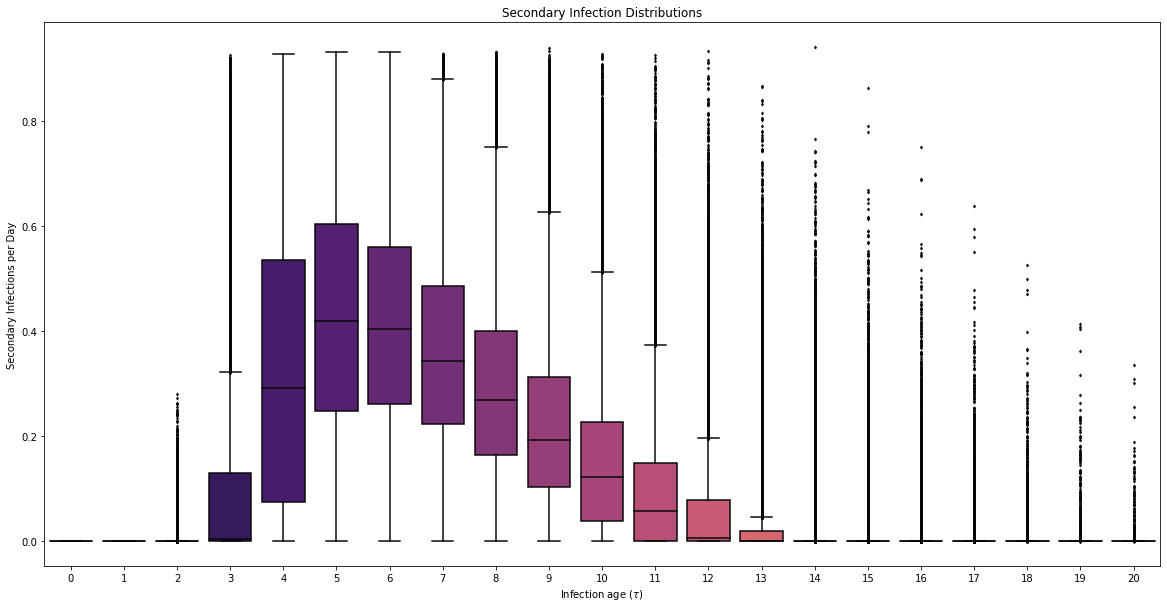
COVID POMDP
Individual Infectiousness
Infection Age
Incident Infections

Need
Test sensitivity is secondary to frequency and turnaround time for COVID-19 surveillance
Larremore et al.
Viral load represented by piecewise-linear hinge function


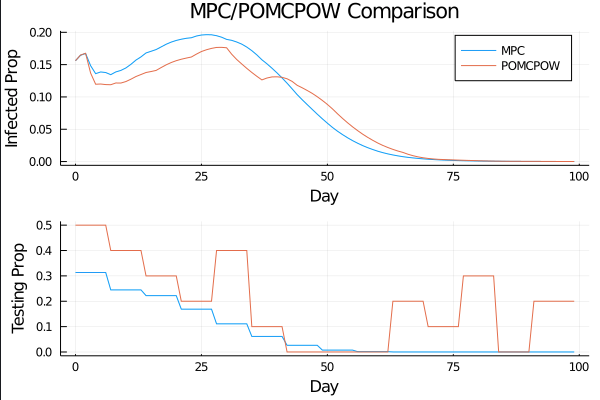
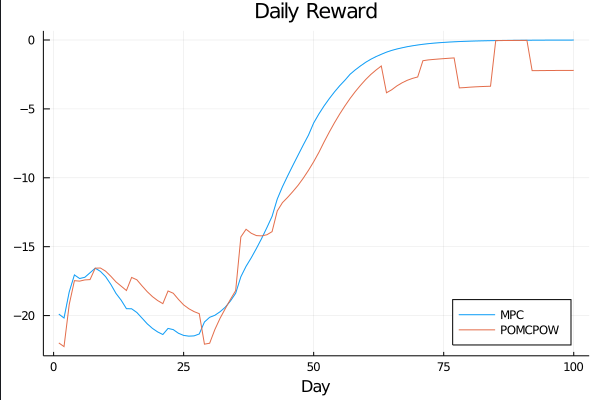
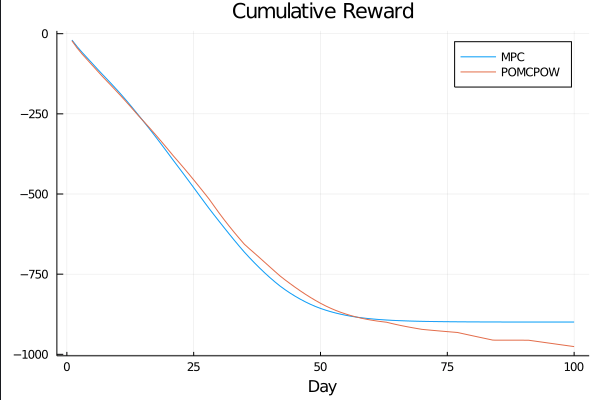

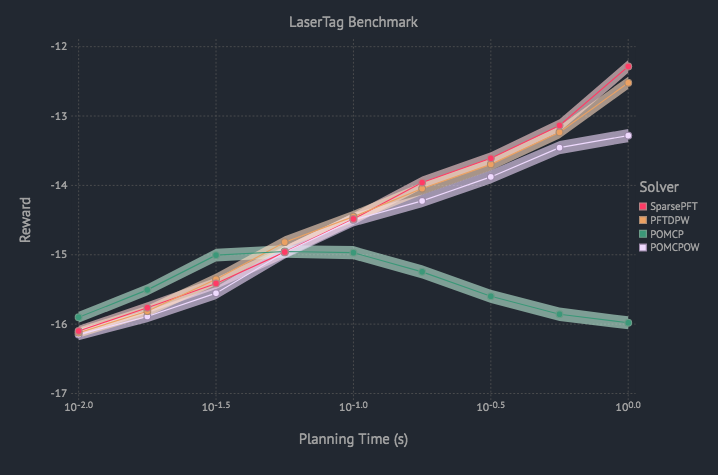
Sparse PFT


Active Information Gathering for Safety
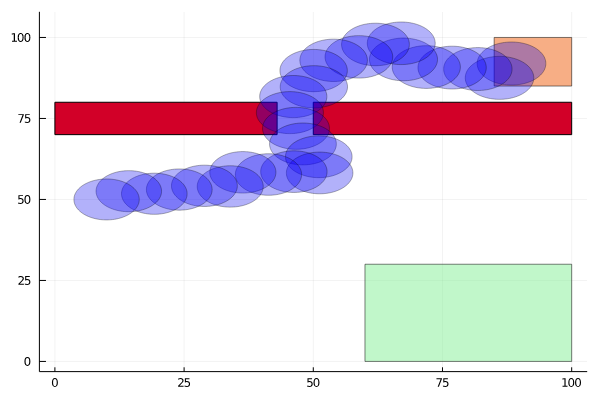
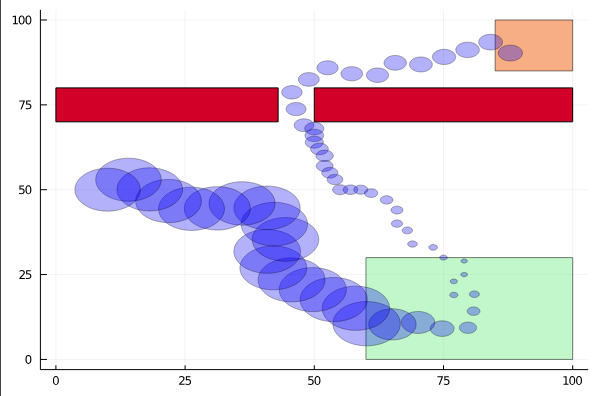


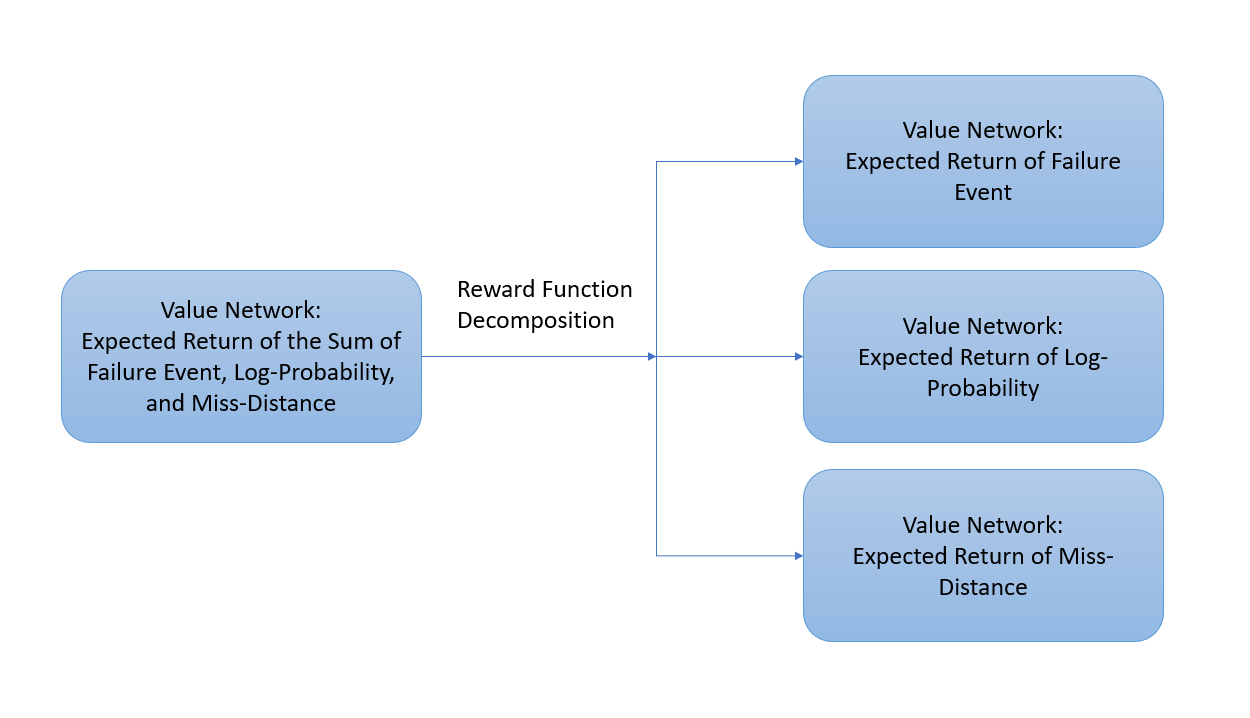
Reward Decomposition for Adaptive Stress Testing

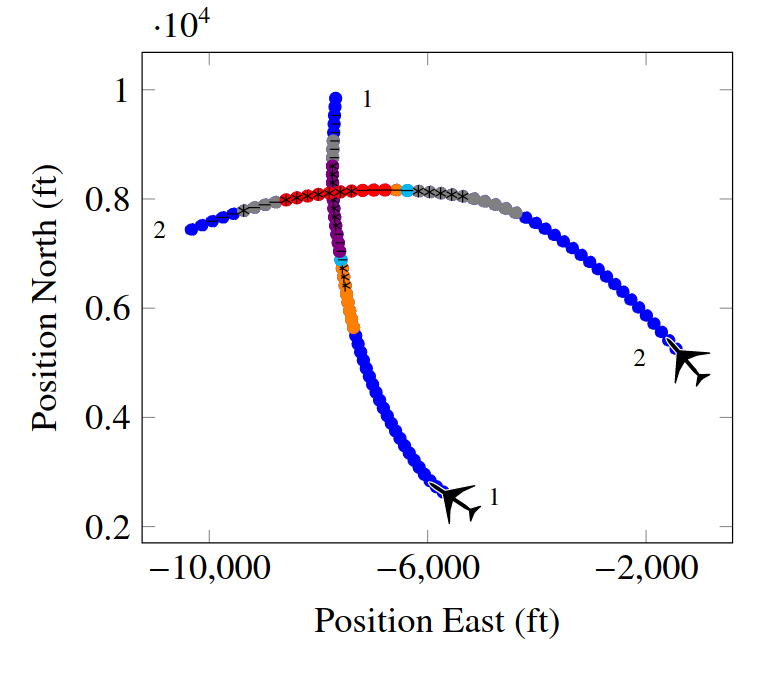


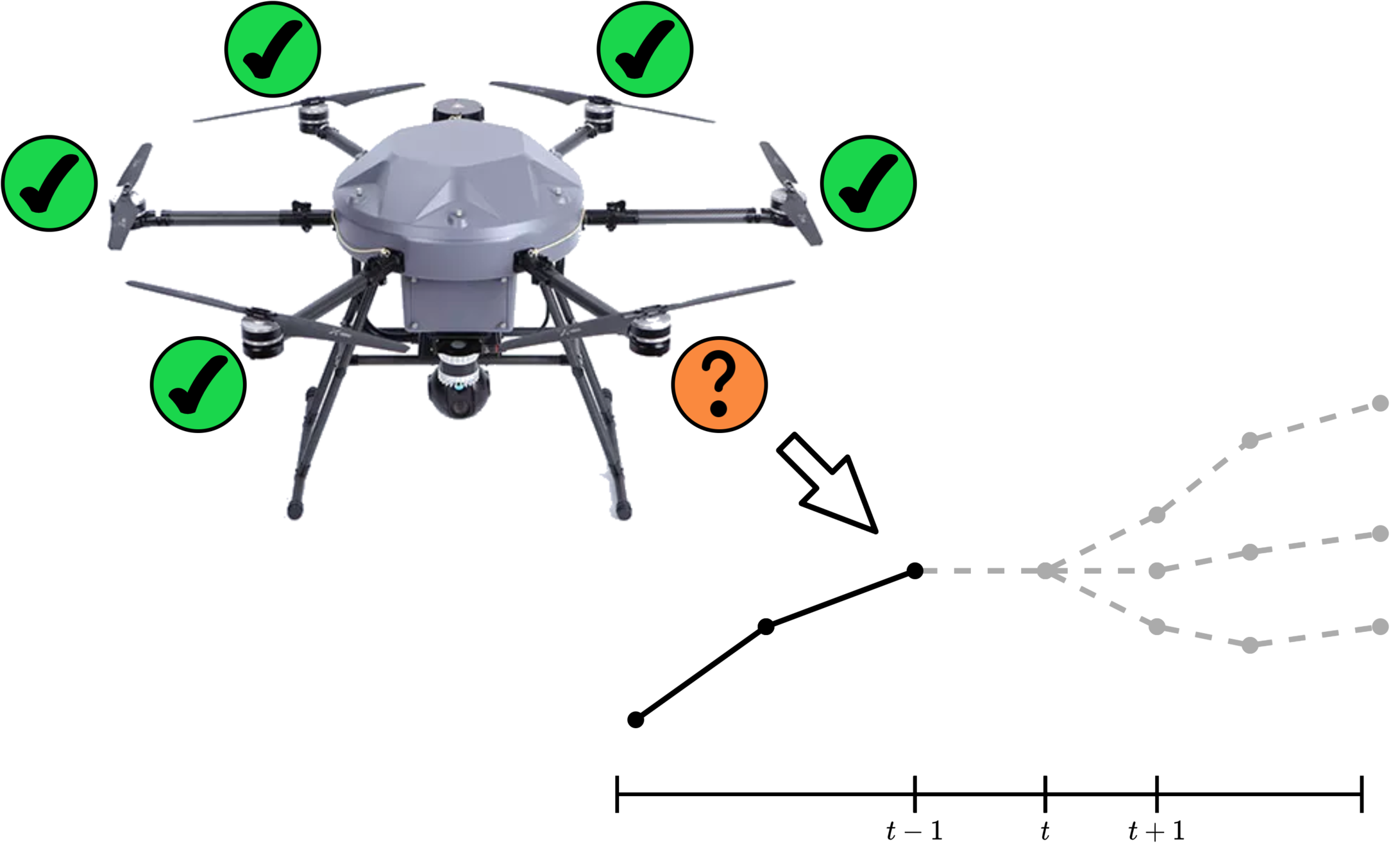
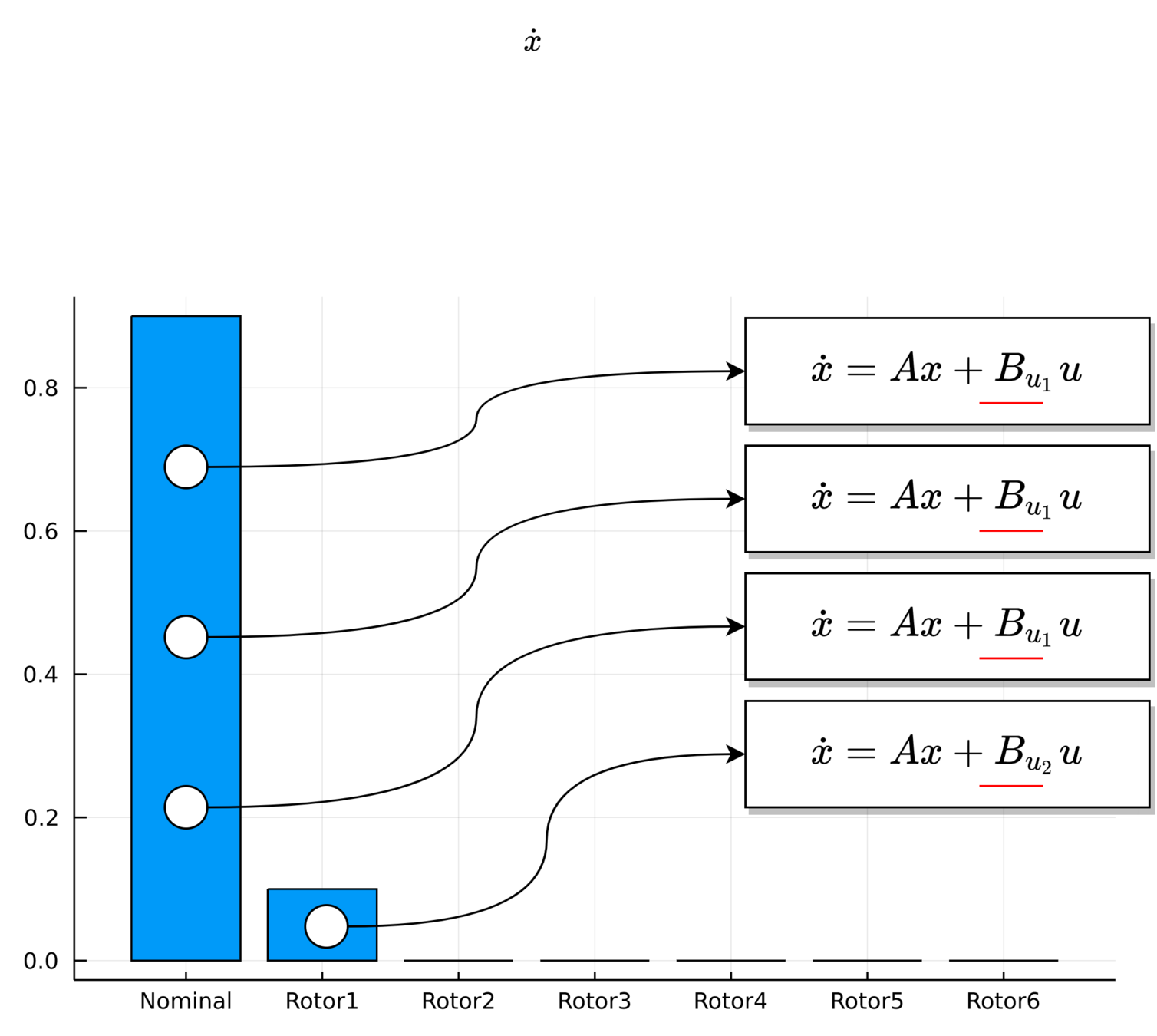
UAV Component Failures
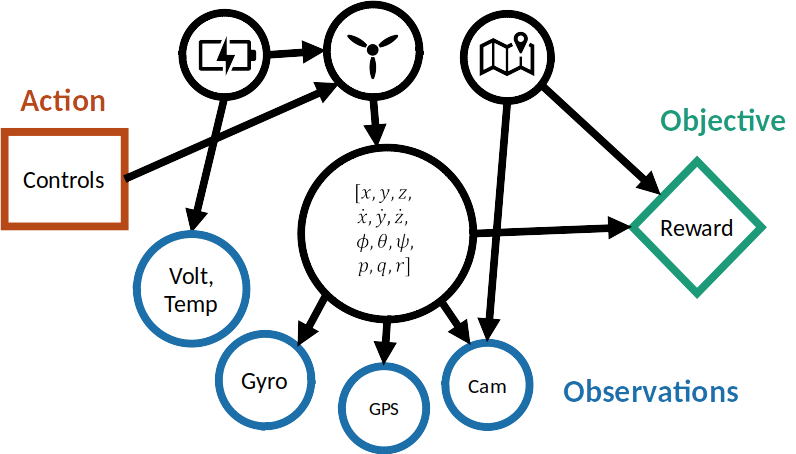
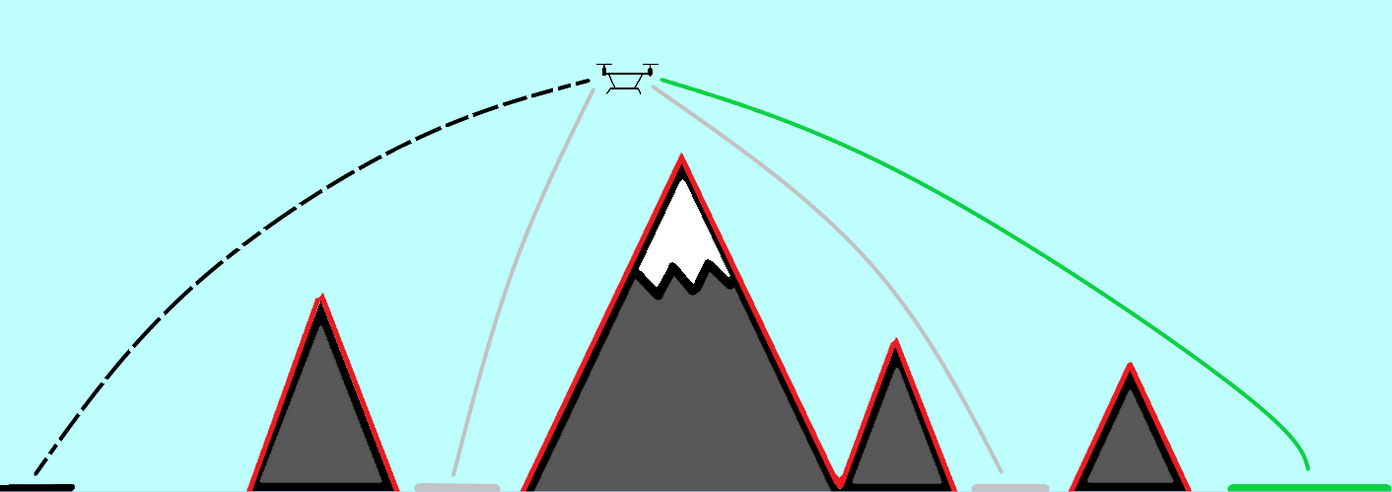

MPC for Intermittent Rotor Failures
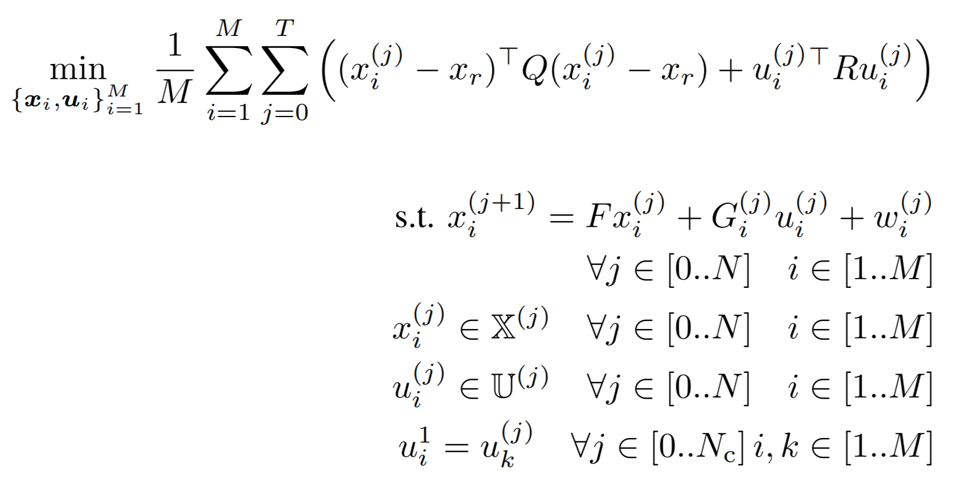

Freshman Seminar
By Zachary Sunberg
Freshman Seminar
- 655



