Safety and Efficiency in Autonomous Vehicles through Planning with Uncertainty
Zachary Sunberg
May 25, 2018



Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl




Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl

Controlling an Autonomous Vehicle is inherently a multi-objective problem
EFFICIENCY
SAFETY
Minimize resource use
(especially time)
Minimize the risk of harm to oneself and others
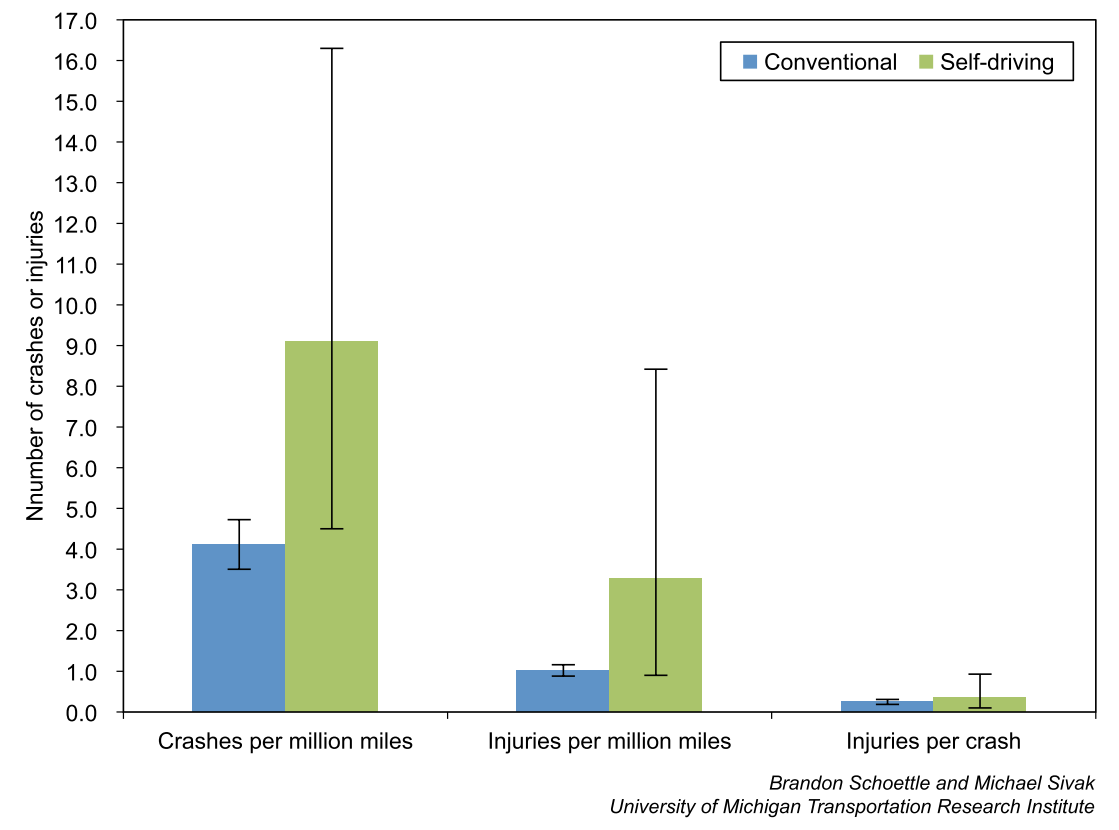
Shoettle and Sivak, "A Preliminary Analysis of Real-World Crashes Involving Self-Driving Vehicles" UMTRI-2015-34


Two extremes:
Objective Function
$$R(s_t, a_t) = R_\text{E}(s_t, a_t) + \lambda R_\text{S}(s_t, a_t)$$
Safety
Weight
Efficiency
\[\text{maximize} \quad E \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right]\]
Objective Function
Safety
Better Performance
Model \(M_2\), Algorithm \(A_2\)
Model \(M_1\), Algorithm \(A_1\)
Efficiency
$$R(s_t, a_t) = R_\text{E}(s_t, a_t) + \lambda R_\text{S}(s_t, a_t)$$
Safety
Weight
Efficiency
Dynamic Model: Types of Uncertainty
OUTCOME
MODEL
STATE




Markov Model
- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}\) - Transition probability distributions
Markov Decision Process (MDP)
- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward

Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward
- \(\mathcal{O}\) - Observation space
- \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution
Contributions
- Quantified the performance price of certifiability for a UAV collision avoidance system and showed how to reduce it.
- Quantified the safety and efficiency advantage of planning with internal states.
- Developed online algorithms for continuous POMDPs.
- Showed that current solvers and naive double progressive widening are suboptimal.
- Used weighted particle filtering to achieve first performance better than QMDP with POMCPOW.
- Led development of POMDPs.jl






Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl

Trusted and Optimized UAV Collision Avoidance

Challenge: Certification
- Government agencies and vehicle operators often seek certification that a control system will never command a near mid-air collision (NMAC).
- Simple, deterministic algorithms are much easier to certify.

Trusted Resolution Logic
Additional buffer compensates for uncertainty



1.0
1.5
2.0
3.0
4.0
MDP Formulation
Transition: \(\quad \dot{\psi}^{(o)}_t = \frac{g \, \tan \phi^{(o)}_t}{v^{(o)}}\), \(\quad \dot{\psi}^{(i)}_t \sim \mathcal{N}(0, 10^\circ/s)\)
Ownship State
Intruder State
Bank Angle


\(s=\left(x^{(o)}, y^{(o)}, \psi^{(o)}, x^{(i)}, y^{(i)}, \psi^{(i)}, \text{dev}\right)\)
\(a = \phi^{(o)}\), \(\mathcal{A} = \{-45^\circ, -22.5^\circ, 0^\circ, 22.5^\circ, 45^\circ\}\)
\(R(s, a) = -c_\text{step} + r_\text{goal} \, \text{in\_goal}(s) - c_\text{dev} \, \text{dev}(s,a) - \lambda \,\text{nmac}(s) \)
Efficiency
Safety
Solving MDPs and POMDPs - The Value Function
$$\mathop{\text{maximize}} V_\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \bigm| s_0 = s, a_t = \pi(s_t) \right]$$
$$V^*(s) = \max \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$
Involves all future time
Involves only \(t\) and \(t+1\)
\(a \in \mathcal{A}\)
Features


\[\tilde{V}(s) = \beta(s)^\top \theta\]
\[\tilde{V}_{k+1}(s) = \Pi \mathcal{B}[\tilde{V}_k](s)\]
\(45^\circ\)
\(-45^\circ\)
\(\phi=0^\circ\)




Sunberg, Zachary N., Mykel J. Kochenderfer, and Marco Pavone. "Optimized and trusted collision avoidance for unmanned aerial vehicles using approximate dynamic programming." Robotics and Automation (ICRA), 2016 IEEE International Conference on. IEEE, 2016.
Value Function
Policy
Price of certifiability




Trusted Resolution Logic

Directly Optimized Turn Rate
Sunberg, Zachary N., Mykel J. Kochenderfer, and Marco Pavone. "Optimized and trusted collision avoidance for unmanned aerial vehicles using approximate dynamic programming." Robotics and Automation (ICRA), 2016 IEEE International Conference on. IEEE, 2016.
Maintaining certifiability
\[\tilde{\mathcal{A}}(s) = \left\{a \in \mathcal{A} \mid \text{mindist}(s, a) \geq D_\text{NMAC} \right\}\]

Price of certifiability




Trusted Resolution Logic

Directly Optimized Turn Rate

Trusted Optimized Turn Rate




Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl


Sadigh, Dorsa, et al. "Information gathering actions over human internal state." Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference on. IEEE, 2016.
Schmerling, Edward, et al. "Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction." arXiv preprint arXiv:1710.09483 (2017).
Sadigh, Dorsa, et al. "Planning for Autonomous Cars that Leverage Effects on Human Actions." Robotics: Science and Systems. 2016.
Tweet by Nitin Gupta
29 April 2018
https://twitter.com/nitguptaa/status/990683818825736192
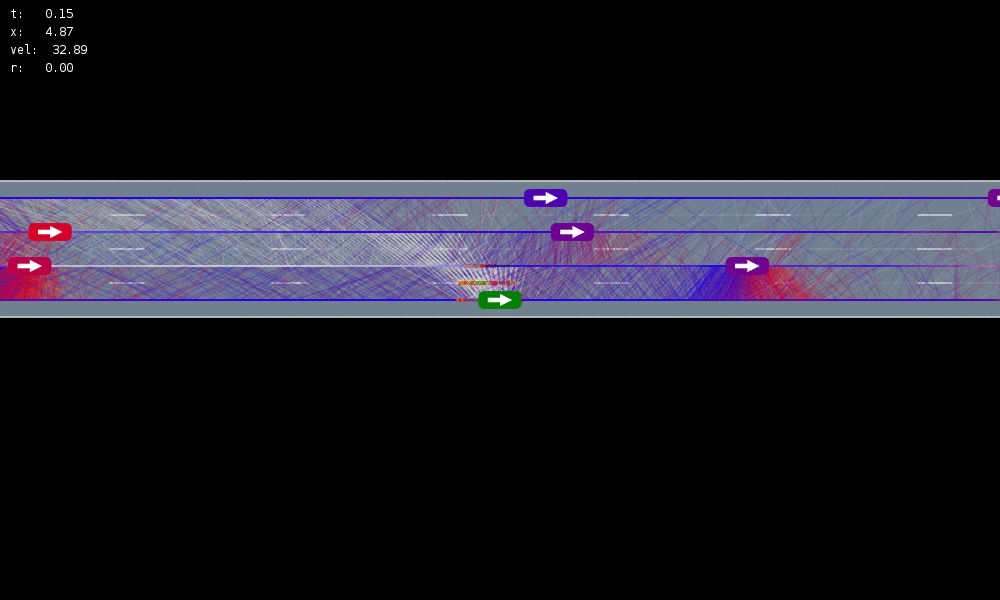
Human Behavior Model: IDM and MOBIL

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).
A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).
A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).
POMDP Formulation
\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)
\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)
\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

Ego physical state
Physical states of other cars
Internal states of other cars
Physical states of other cars

- Actions filtered so they can never cause crashes
- Braking action always available
Efficiency
Safety
Belief
History: all previous actions and observations
\[h_t = (b_0, a_0, o_1, a_1, o_2, ..., a_{t-1}, o_t)\]
Belief: probability distribution over \(\mathcal{S}\) encoding everything learned about the state from the history
\[b_t(s) = P(s_t=s \mid h_t)\]
A POMDP is an MDP on the belief space
Solving MDPs and POMDPs - Offline vs Online



ONLINE
OFFLINE
Value Iteration
Sequential Decision Trees
QMDP
\[Q_{MDP}(b, a) = \sum_{s \in \mathcal{S}} Q_{MDP}(s,a) b(s) \geq Q^*(b,a)\]
Equivalent to assuming full observability on the next step
Will not take costly exploratory actions
$$Q_\pi(b,a) = E \left[ \sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \bigm| s_0 = s, a_0 = a\right]$$








All drivers normal





Outcome only
Omniscient
Mean MPC
QMDP
POMCPOW
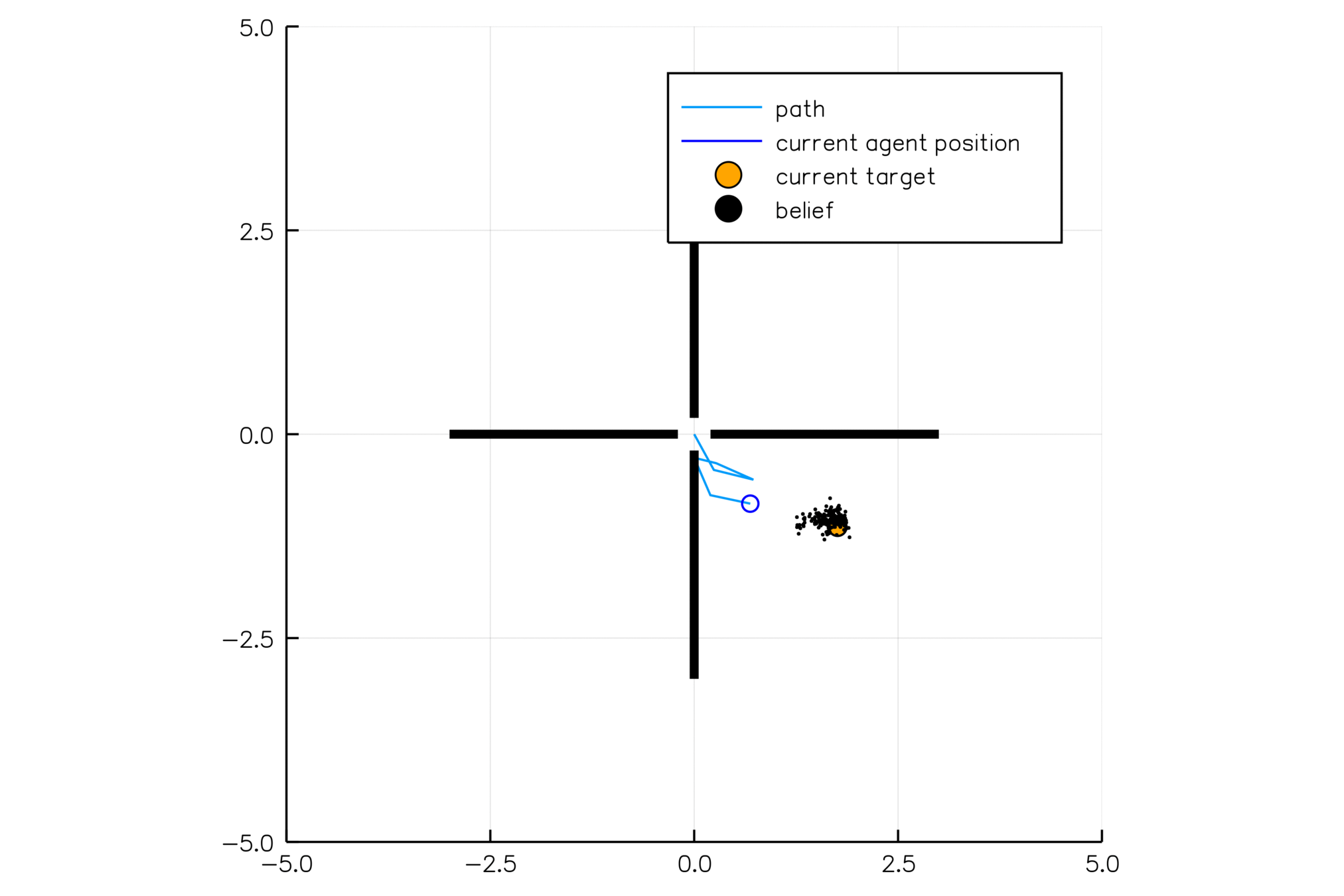
Simulation results





All drivers normal




Omniscient
Mean MPC
QMDP
POMCPOW



Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl


Monte Carlo Tree Search
Image by Dicksonlaw583 (CC 4.0)
POMCP
- Uses simulations of histories instead of full belief updates
- Each belief is implicitly represented by a collection of unweighted particles


Silver, David, and Joel Veness. "Monte-Carlo planning in large POMDPs." Advances in neural information processing systems. 2010.
Ross, Stéphane, et al. "Online planning algorithms for POMDPs." Journal of Artificial Intelligence Research 32 (2008): 663-704.
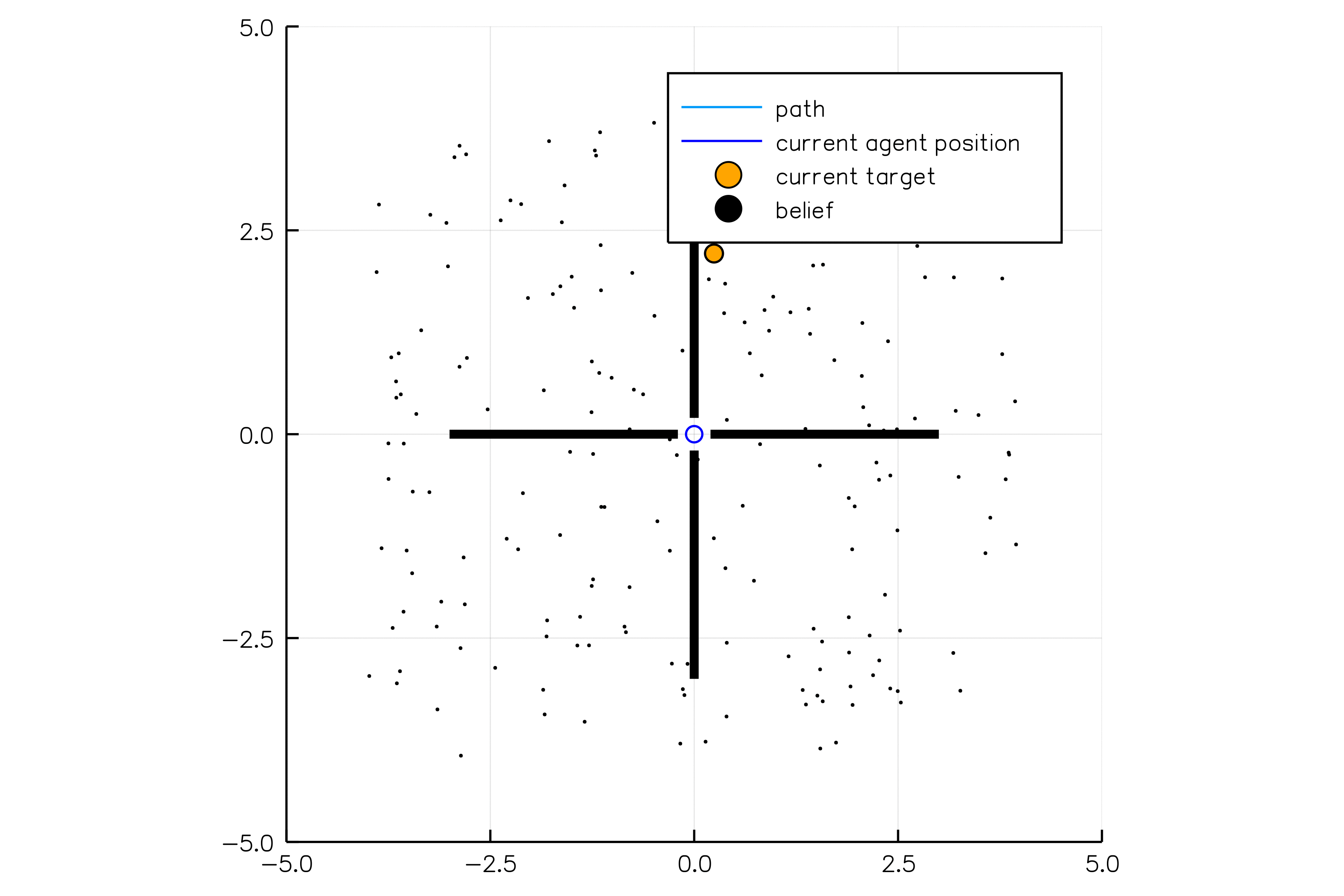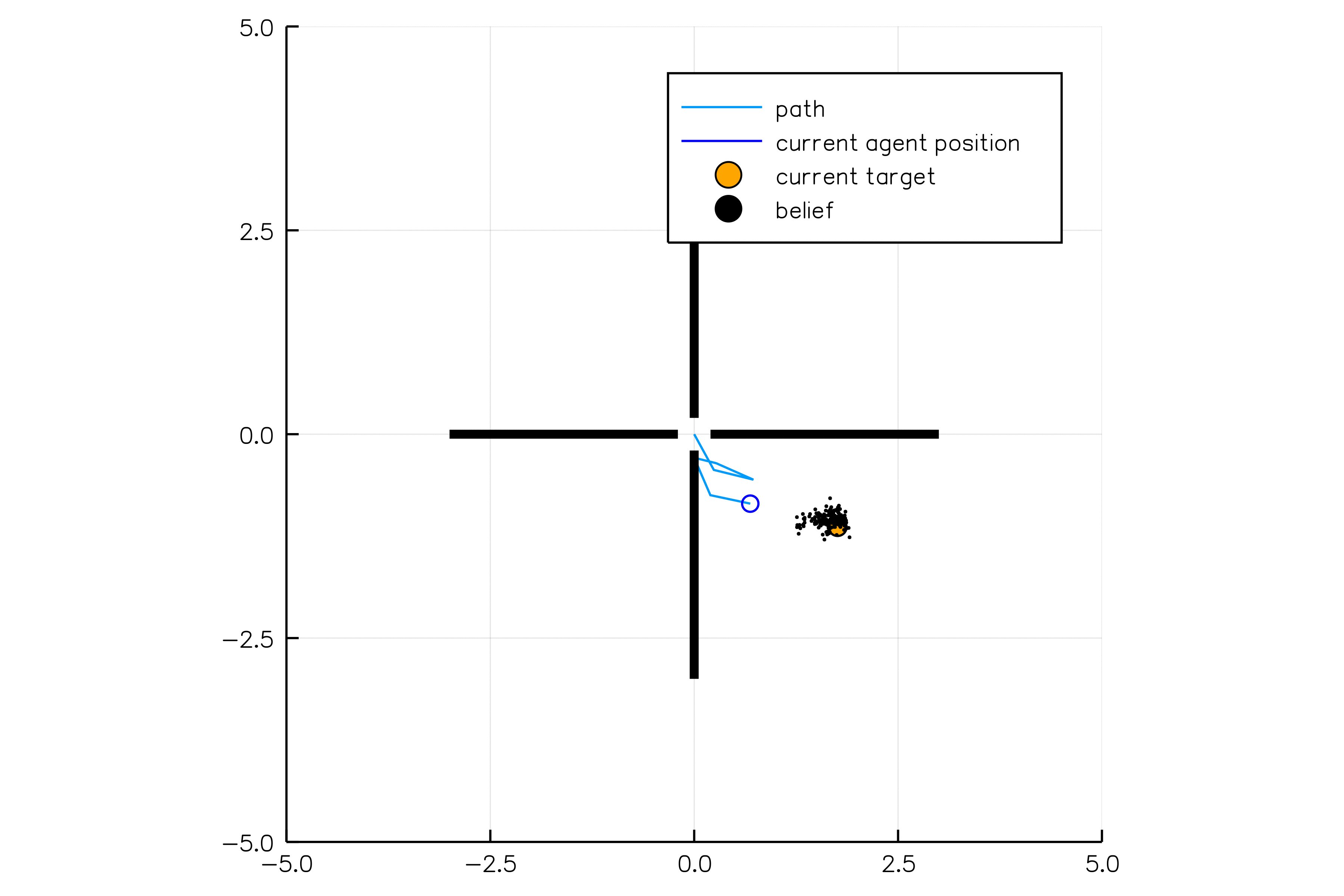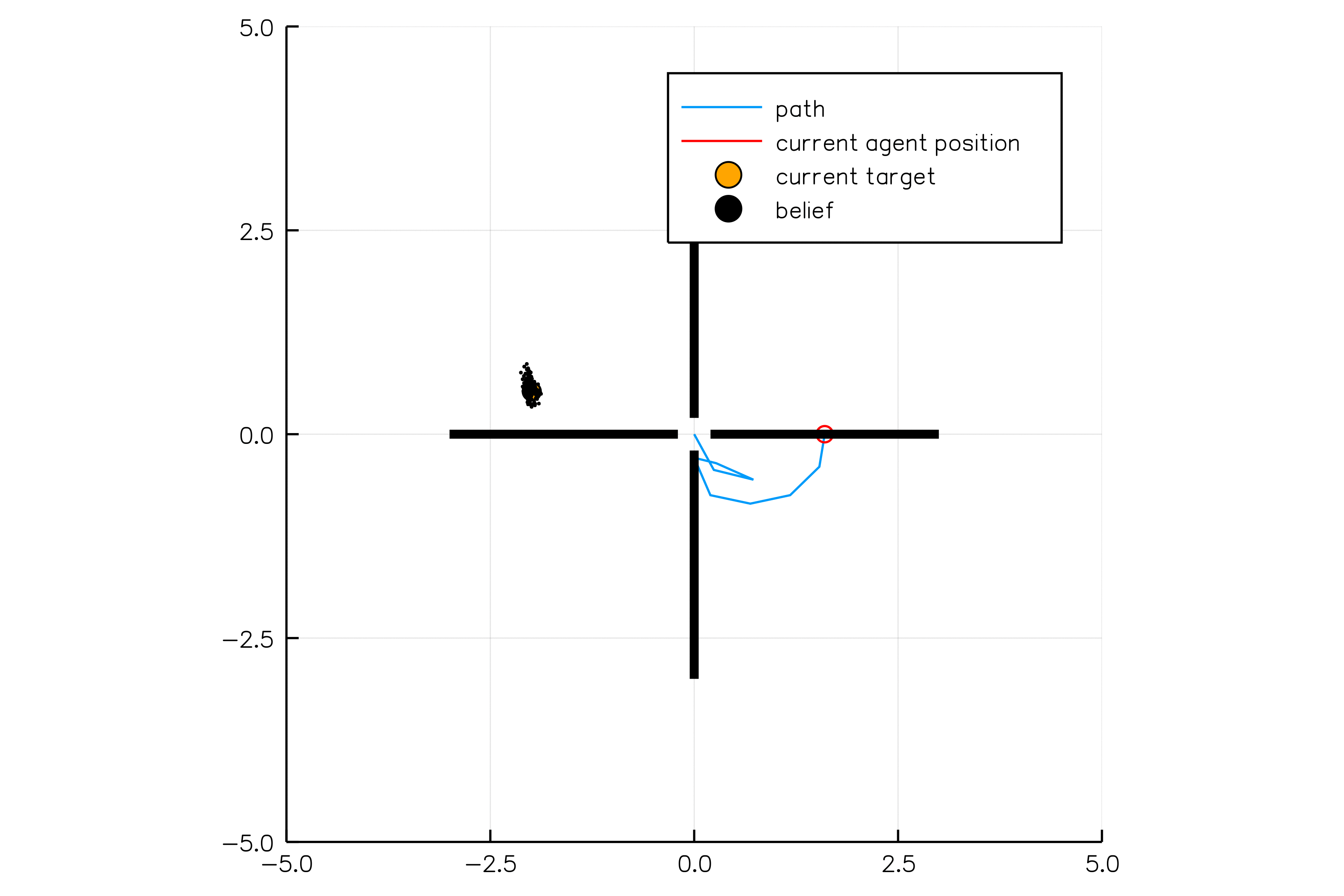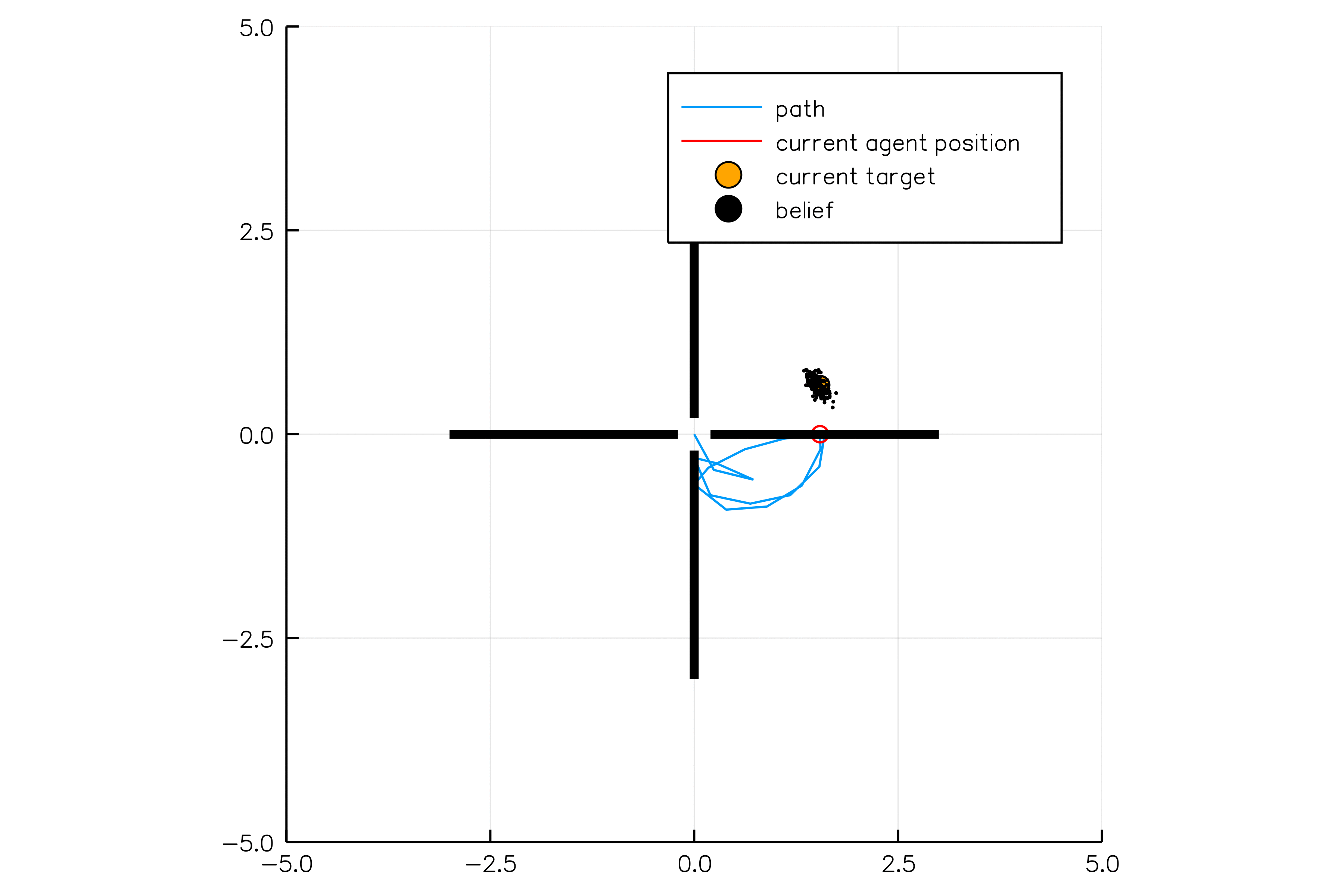
Light-Dark Problem

State
Timestep
Accurate Observations
Goal: \(a=0\) at \(s=0\)
Optimal Policy
Localize
\(a=0\)
[ ] An infinite number of child nodes must be visited
[ ] Each node must be visited an infinite number of times
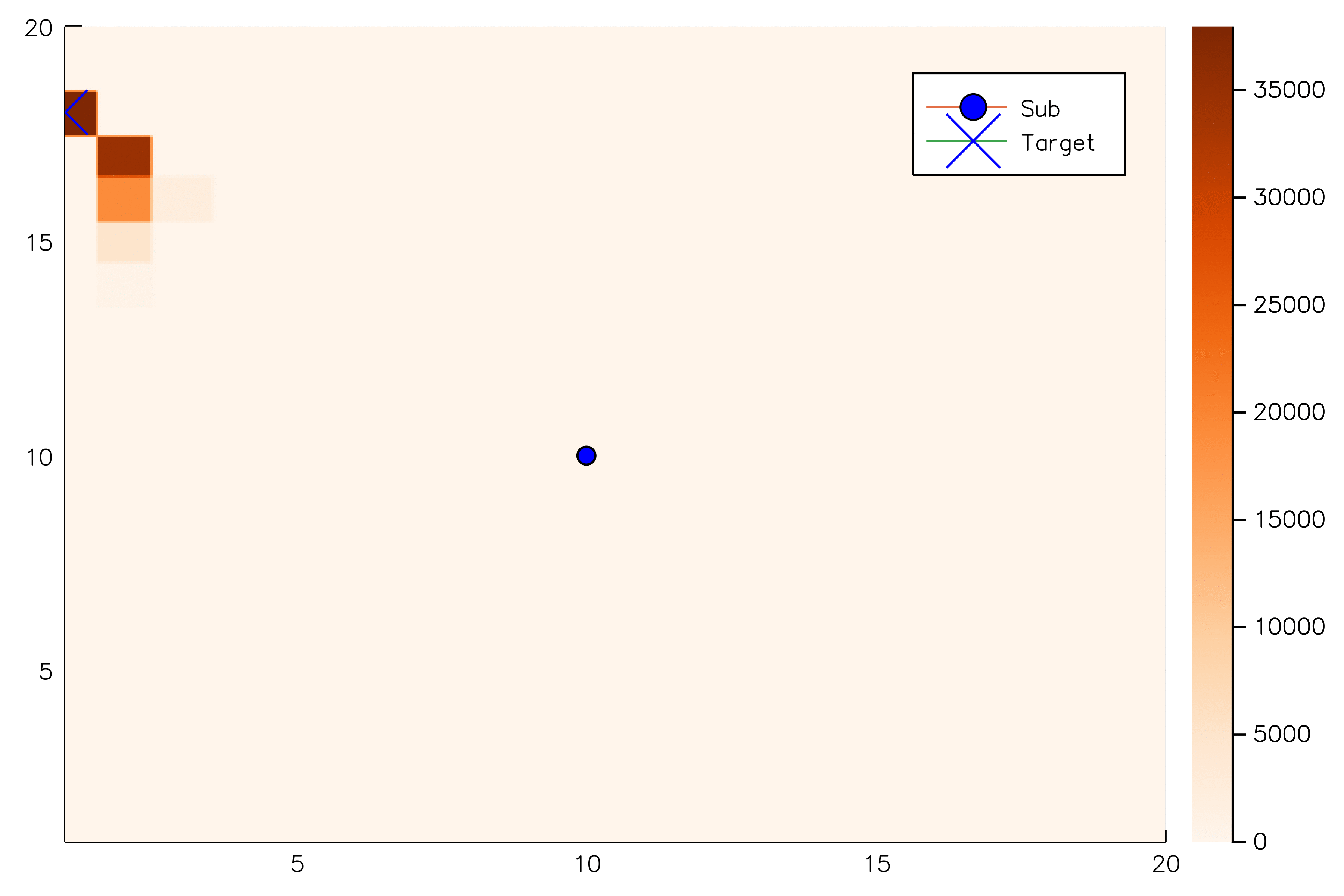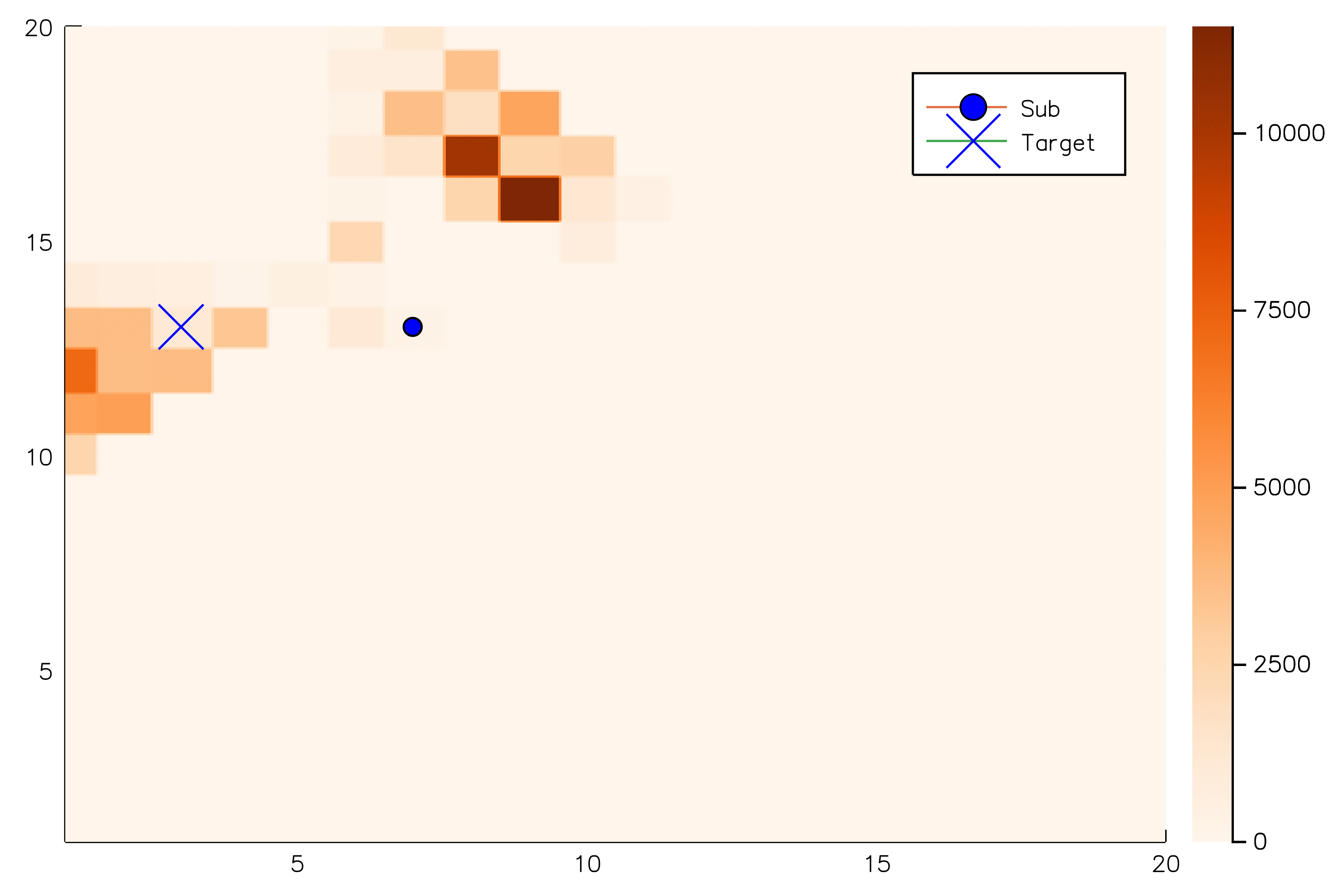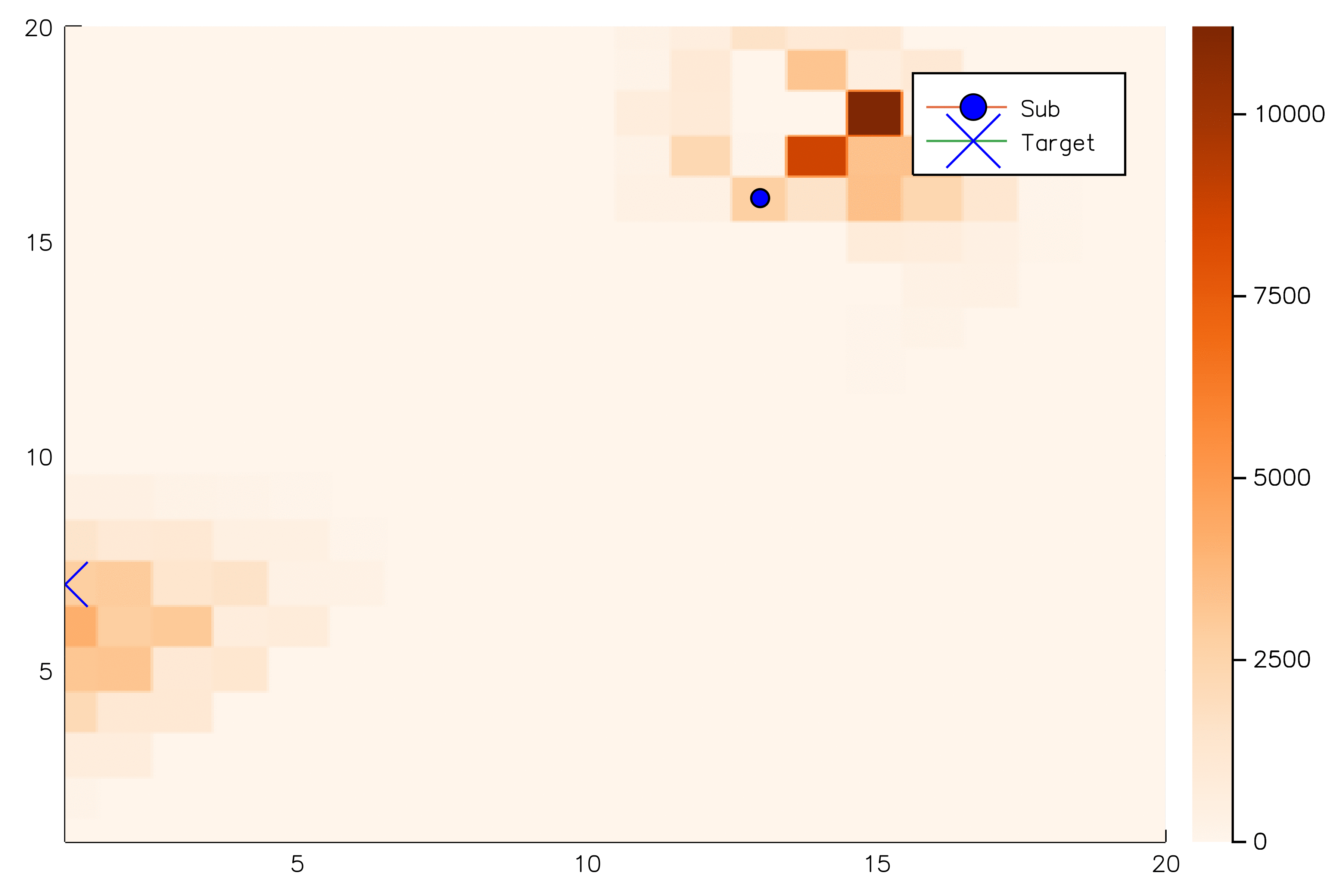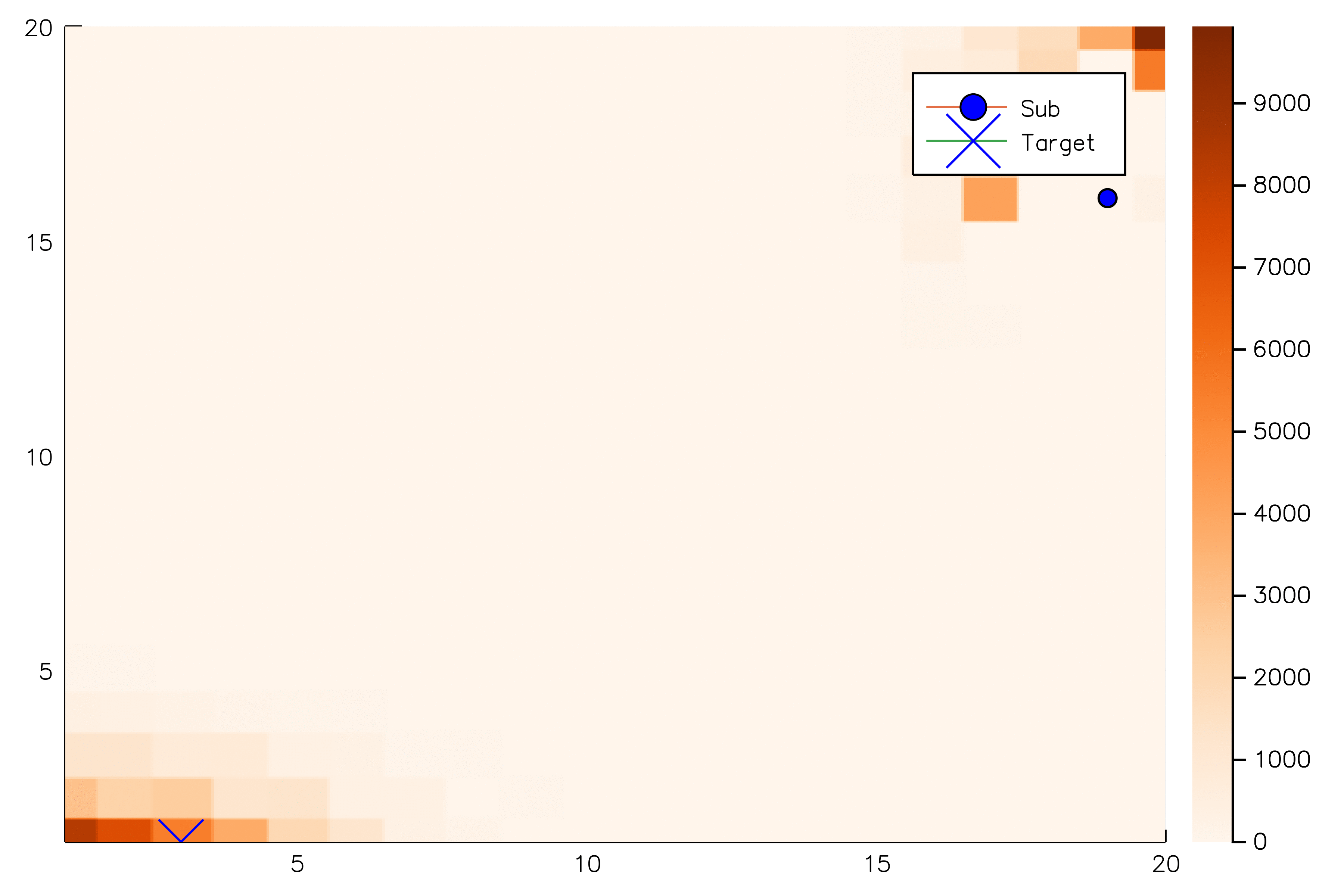
Solving continuous POMDPs - POMCP fails
[1] Adrien Coutoux, Jean-Baptiste Hoock, Nataliya Sokolovska, Olivier Teytaud, Nicolas Bonnard. Continuous Upper Confidence Trees. LION’11: Proceedings of the 5th International Conference on Learning and Intelligent OptimizatioN, Jan 2011, Italy. pp.TBA. <hal-00542673v2>
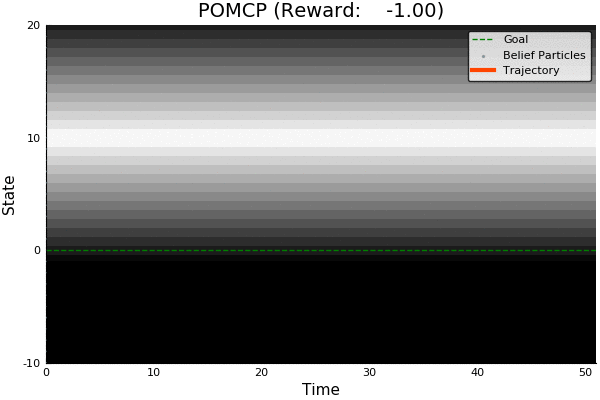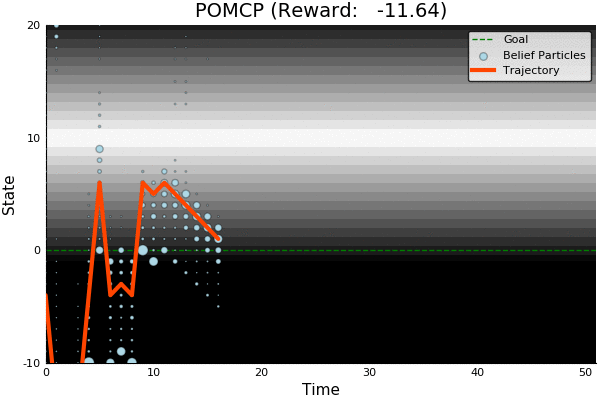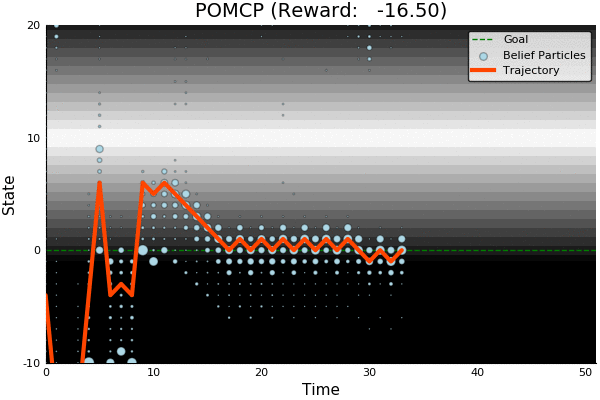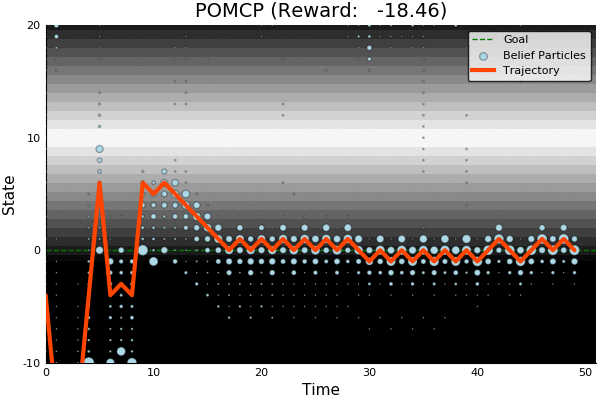

POMCP
✔
✔
Limit number of children to
\[k N^\alpha\]
Necessary Conditions for Consistency [1]



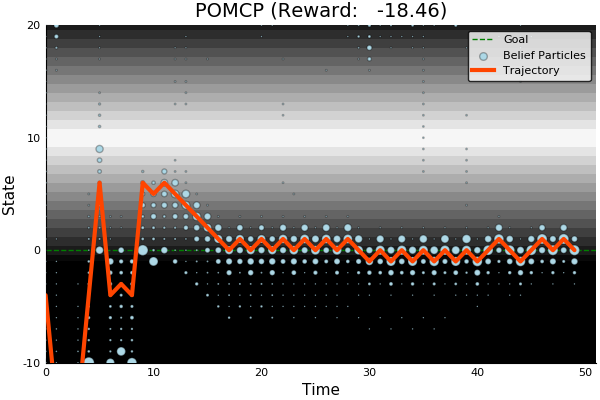
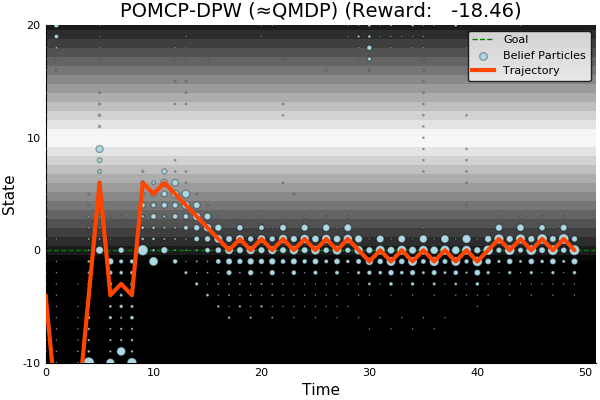
POMCP
POMCP-DPW
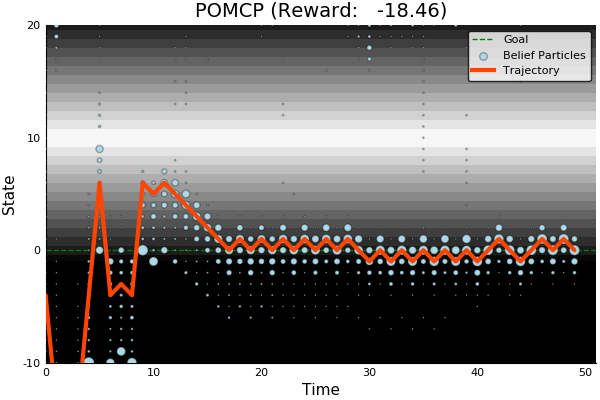

POMCP-DPW converges to QMDP
Proof Outline:
-
Observation space is continuous → observations unique w.p. 1.
-
(1) → One state particle in each belief, so each belief is merely an alias for that state
-
(2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state
-
Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP



Sunberg, Z. N. and Kochenderfer, M. J. "Online Algorithms for POMDPs with Continuous State, Action, and Observation Spaces", ICAPS (2018)

POMCP-DPW
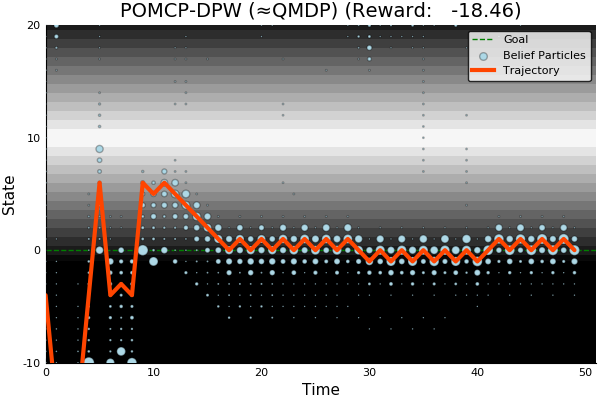
[ ] An infinite number of child nodes must be visited
[ ] Each node must be visited an infinite number of times
[ ] An infinite number of particles must be added to each belief node
✔
✔
Necessary Conditions for Consistency
Use \(Z\) to insert weighted particles
✔


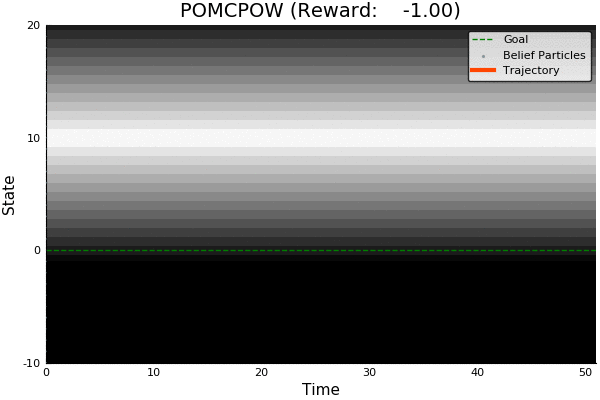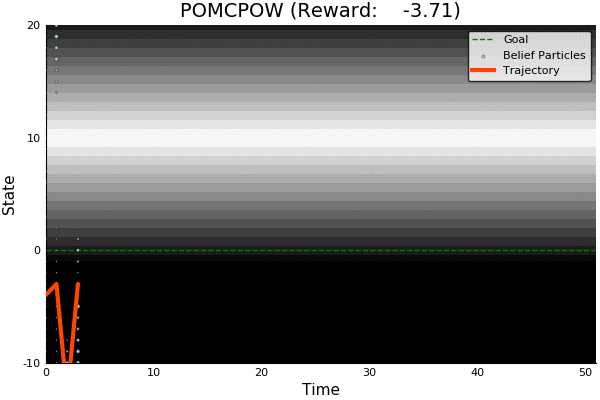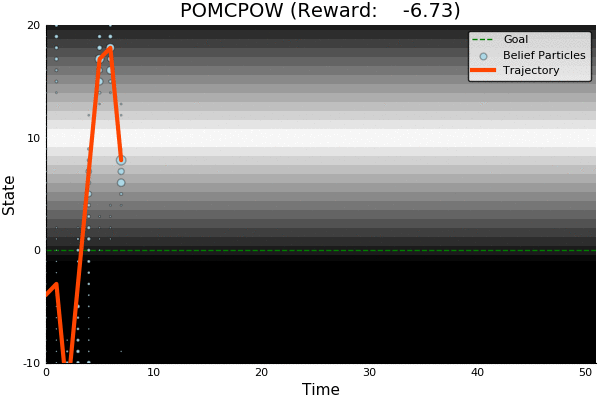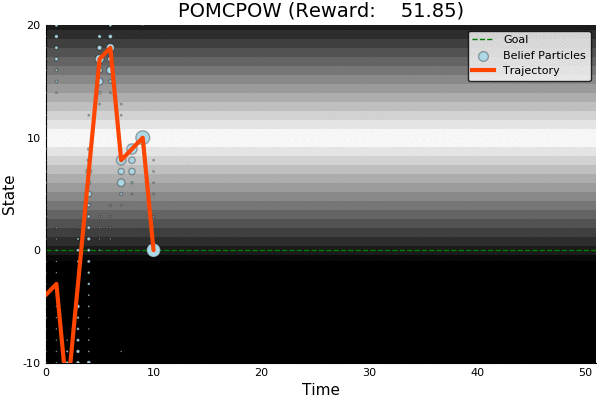



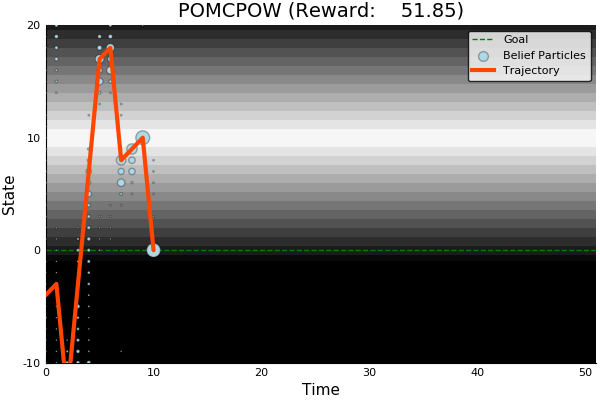
POMCP
POMCP-DPW
POMCPOW



Ye, Nan, et al. "DESPOT: Online POMDP planning with regularization." Journal of Artificial Intelligence Research 58 (2017): 231-266.
















Introduction
UAV Collision Avoidance
Lane Changing with Internal States
Solving Continuous POMDPs
POMDPs.jl

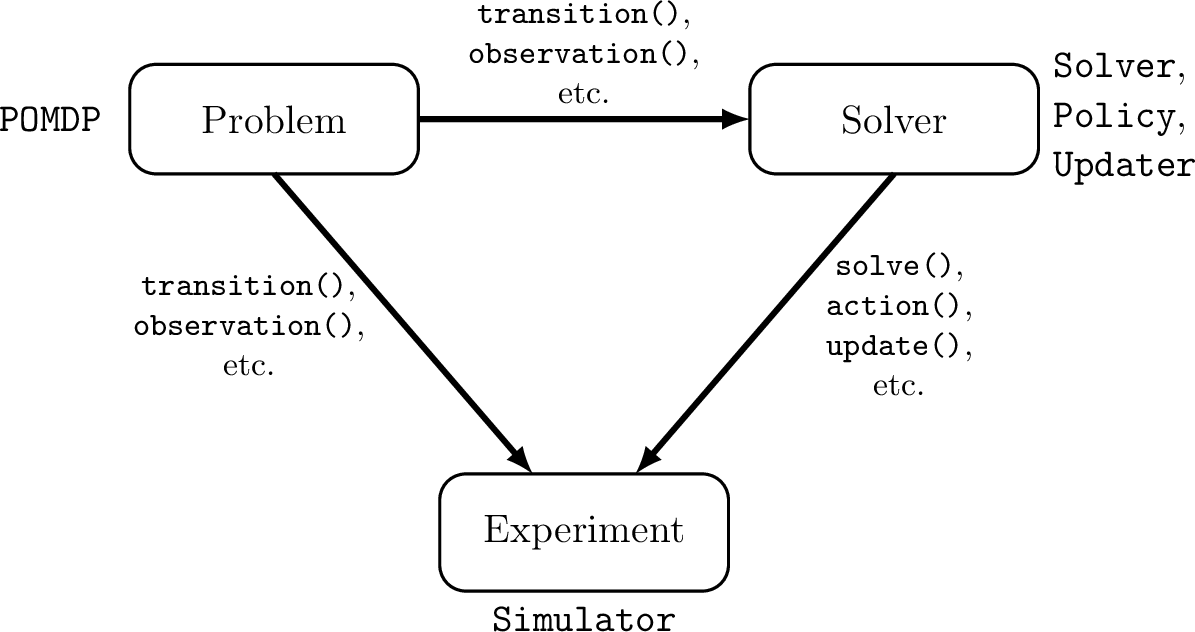

POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia
Challenges for POMDP Software
- POMDPs are computationally difficult.
- There is a huge variety of
- Problems
- Continuous/Discrete
- Fully/Partially Observable
- Generative/Explicit
- Simple/Complex
- Solvers
- Online/Offline
- Alpha Vector/Graph/Tree
- Exact/Approximate
- Domain-specific heuristics
- Problems

Explicit
Generative
\(s,a\)
\(s', o, r\)
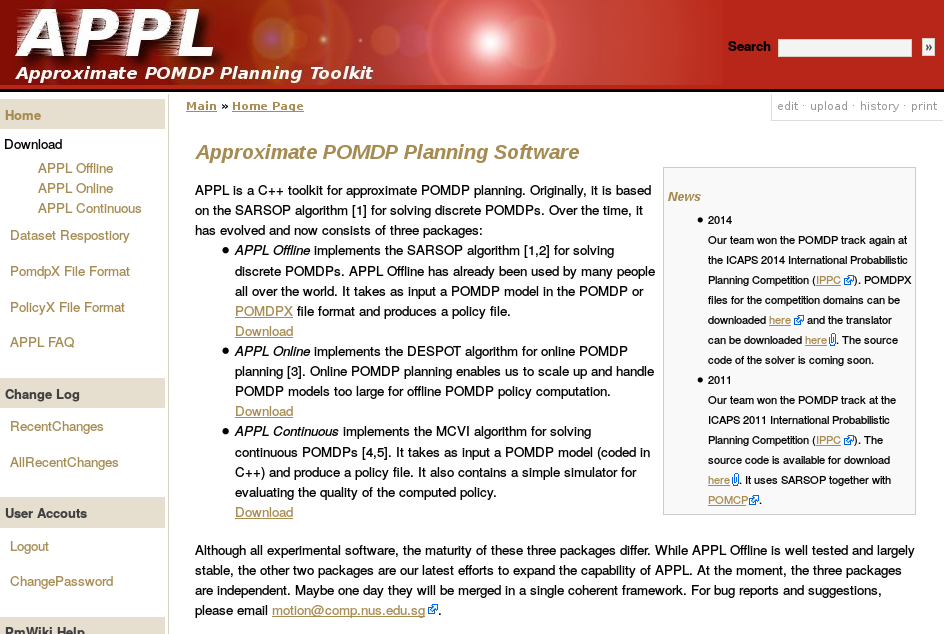
Previous C++ framework: APPL
"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."



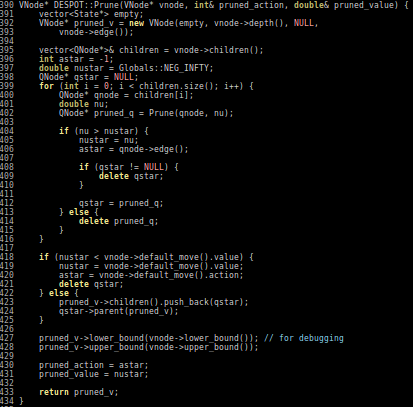
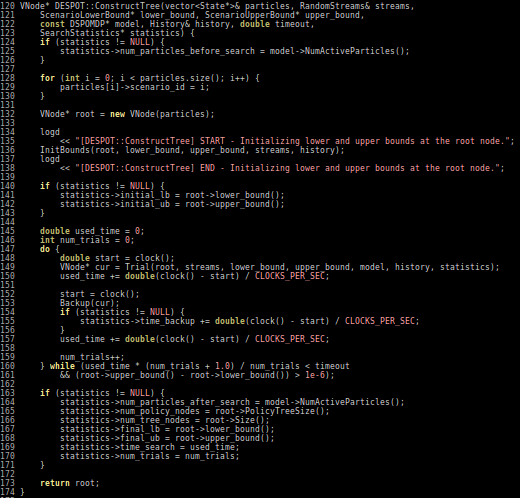
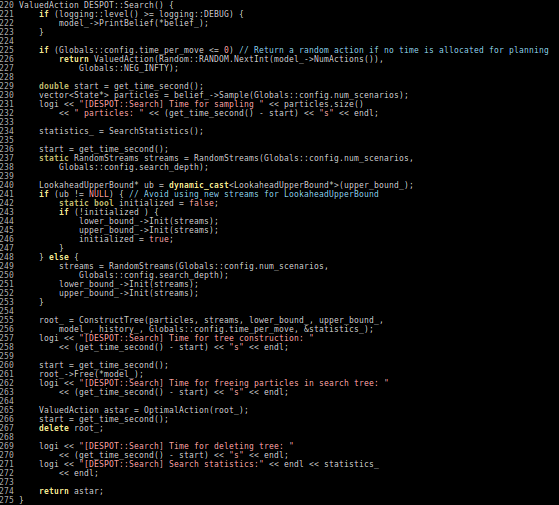


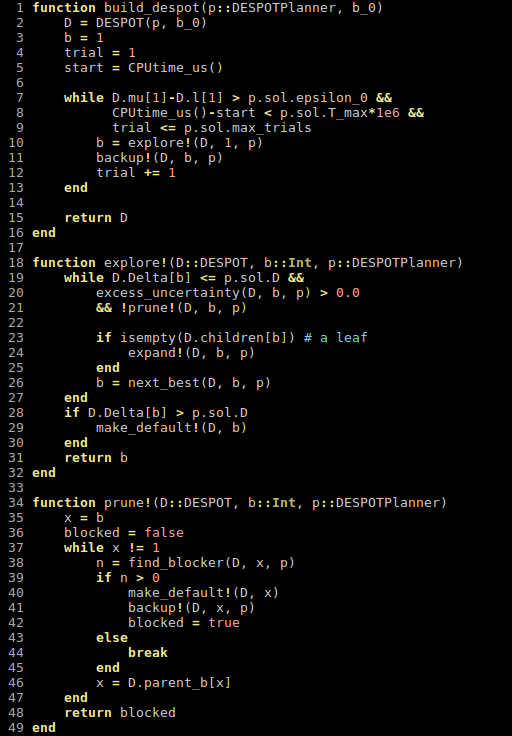
Conclusions
- Solving UAV collision avoidance problems as MDPs offline offers safety an efficiency improvements even when combined with conservative safety constraints
- In a simplified highway lane-changing scenario, there is a significant performance gap caused by ignoring the internal states of other drivers
- This gap can be largely closed using POMDP planning
- Current online POMDP solvers and naive double progressive widening are unable to solve POMDPs with continuous observation spaces that require costly exploration
- POMCPOW and PFT-DPW are the first algorithms to obtain better-than-QMDP performance on such problems
- POMDPs.jl provides a fast and easy to use framework for POMDP research and education



Peer-Reviewed Publications




Future Work
- Investigate the effects of communication in lane changing with turn signals, "nudging in", etc. in highway lane changing
- Test POMDP lane change planners on driver models learned from real data
- Apply to internal-state-aware planning to simpler situations and test with real vehicles
- Extend DESPOT to handle continuous POMDPs
- Search for theoretical guarantees about the convergence of online continuous POMDP algorithms
- Thoroughly investigate parallelism in online continuous POMDP algorithms
- Implement declarative interfaces for simple problems on top of POMDPs.jl
- Implement better interfaces for classes of factored problems in POMDPs.jl


Acknowledgements
Funding Sources
The content of my thesis reflects my opinions and conclusions, and is not necessarily endorsed by these organizations.


Committee & Mentors








Chris Gerdes
Dorsa Sadigh
Mac Schwager
Dan DeBra
Jon Rogers
Suman Chakravorty
Marco Pavone
Mykel Kochenderfer
ASL and SISL


Church Family

Friends















Happy Birthday Kevin

Family


Thesis Defense
By Zachary Sunberg
Thesis Defense
- 2,775



