Incomplete Information Dynamic Games
Incomplete Information

Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
- \(\mathcal{O}\) - Observation space
- \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution
Alleatory
Epistemic (Static)
Epistemic (Dynamic)
Partially Observable Markov Game
Alleatory
Epistemic (Static)
Epistemic (Dynamic)
Interaction
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, \bm{a})\) - Transition probability distribution
- \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
- \(R^i(s, \bm{a})\) - Reward function
- \(\mathcal{O}^i, \, i \in 1..k\) - Observation space
- \(Z(o^i \mid \bm{a}, s')\) - Observation probability distribution

Partially Observable Markov Game
Hierarchy of Problems

Belief updates?
Reduction to Simple Game
Reduction to Simple Game

Pruning in Dynamic Programming


Extensive Form Game
(Alternative to POMGs that is more common in the literature)
- Similar to a minimax tree for a turn-taking game
- Chance nodes
- Information sets
Extensive Form Game
(Alternative to POMGs that is more common in the literature)
- Similar to a minimax tree for a turn-taking game
- Chance nodes
- Information sets
Extensive Form Game
Extensive-form game definition (\(h\) is a sequence of actions called a "history"):
- Finite set of \(n\) players, plus the "chance" player
- \(P(h)\) (player at each history)
- \(A(h)\) (set of actions at each history)
- \(I(h)\) (information set that each history maps to)
- \(U(h)\) (payoff for each leaf node in the game tree)
King-Ace Poker Example
- 4 Cards: 2 Aces, 2 Kings
- Each player is dealt a card
- P1 can either raise (\(r\)) the payoff to 2 points or check (\(k\)) the payoff at 1 point
- If P1 raises, P2 can either call (\(c\)) Player 1's bet, or fold (\(f\)) the payoff back to 1 point
- The highest card wins
King-Ace Poker Example
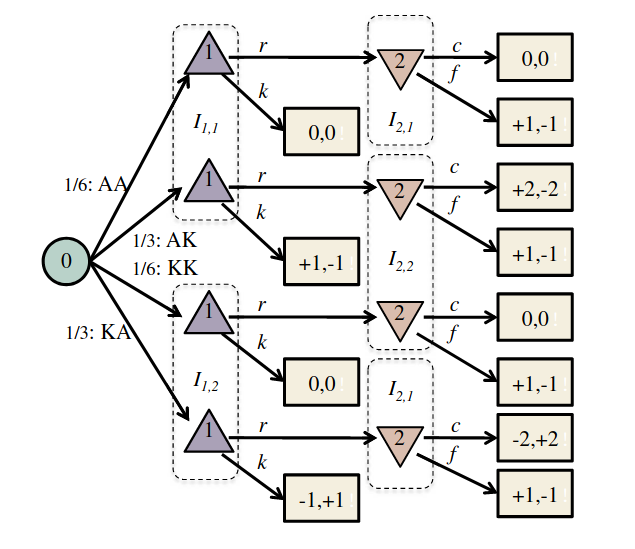
- 4 Cards: 2 Aces, 2 Kings
- Each player is dealt a card
- P1 can either raise (\(r\)) the payoff to 2 points or check (\(k\)) the payoff at 1 point
- If P1 raises, P2 can either call (\(c\)) Player 1's bet, or fold (\(f\)) the payoff back to 1 point
- The highest card wins
Extensive to Matrix Form


Exponential in number of info states!
A more interesting example: Kuhn Poker

Fictitious Play in Extensive Form Games


Heinrich et al. 2015 "Fictitious Self Play in Extensive-Form Games"
Deep Stack: Scaling to Heads Up No Limit Texas Hold 'Em

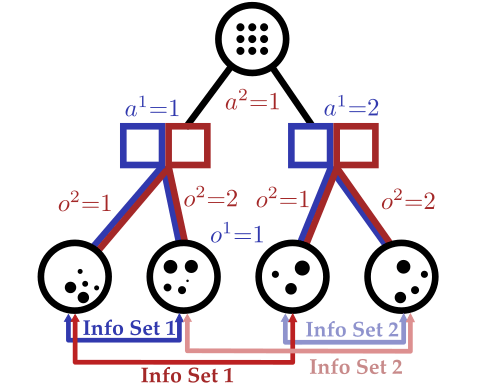
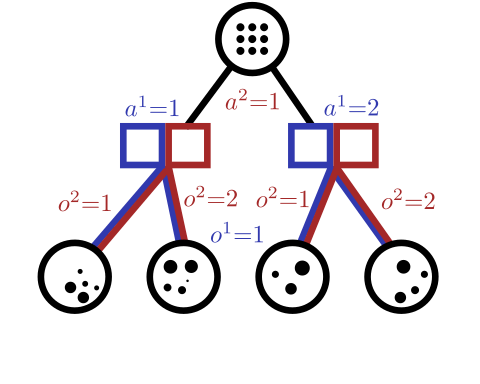
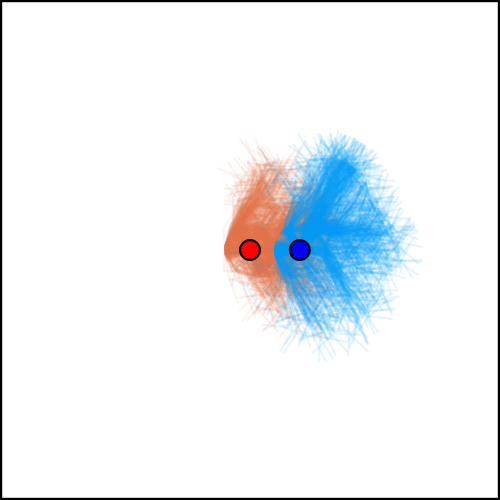
[Becker & Sunberg, AAMAS 2025]
Tree-Based Planning in POSGs
Our approach: combine particle filtering and information sets
Joint Belief
Joint Action
Alpha Star



Deep Nash

Stratego


255 Incomplete Information Games
By Zachary Sunberg
255 Incomplete Information Games
- 573



