Particle Filters
POMDP Sense-Plan-Act Loop
Environment
Option 2: Belief Updater
Policy
\(b\)
\(a\)
True State
\(s = TL\)
Observation \(o = TL\)
Belief: \(b_t = P(s_t \mid h_t)\)
\(TL\)
\(TR\)
(Options below)
Option 1: History
\(h\)
History: \(h_t = (b_0, a_0, o_1, a_1, \ldots a_{t-1}, o_{t})\)
Review: Bayesian Filter
\(b_t(s) = P(s_t = s \mid h_t)\)
\(b' = \tau (b, a, o)\)
\[b'(s') \propto Z(o \mid a, s') \sum_{s} T(s' \mid s, a) \, b(s)\]
Rejection Particle Filter
Weighted Particle Filtering
Weighted Particle Filtering
Weighted Particle Filtering
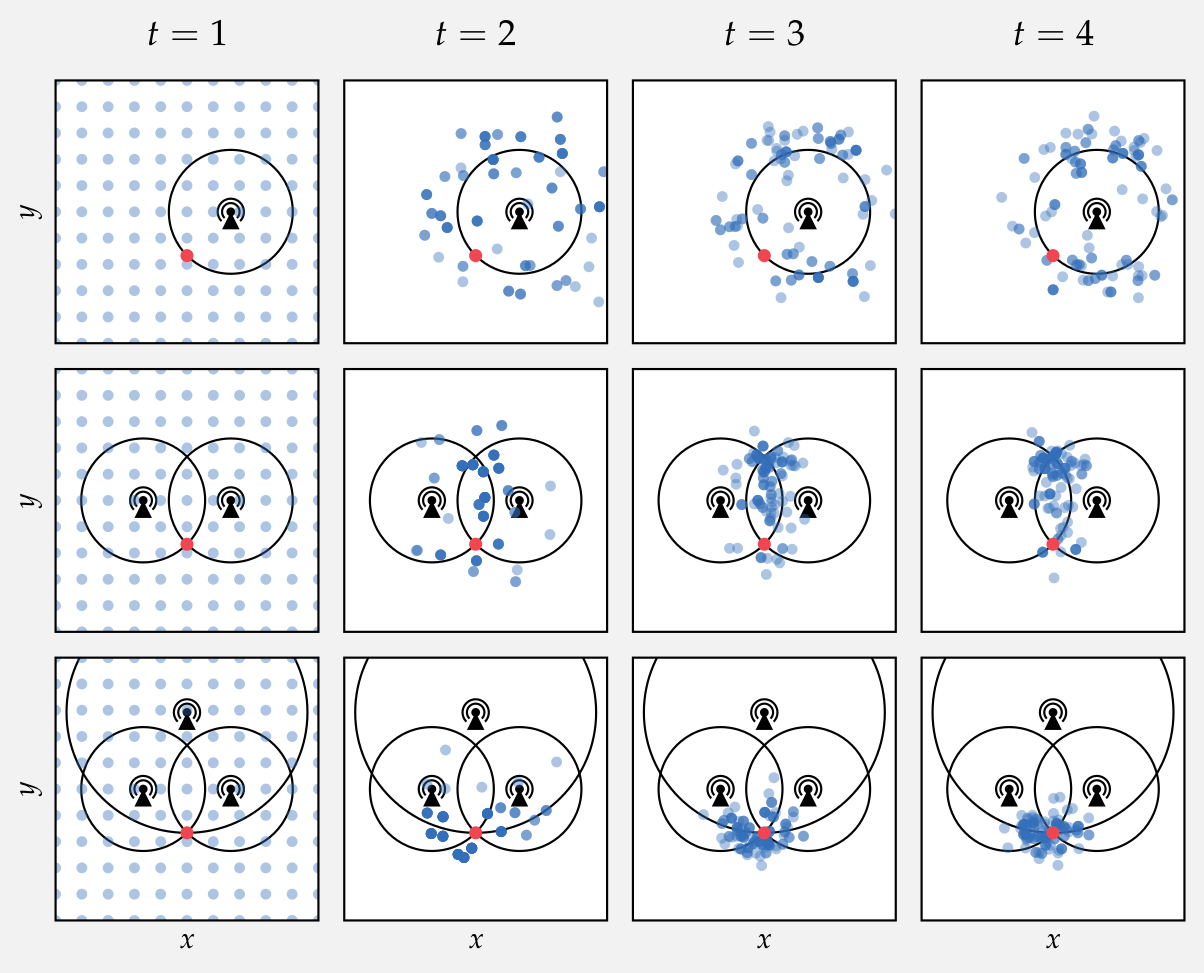
Particle Depletion
Solution: Domain specific particle injection based on:
- Weights
- Particle Diversity
Important Particle Filter Properties
- When only estimating the reward, the number of particles does NOT need to scale exponentially with the dimension (i.e. \(n \neq k^d\))
- Implementation should have \(O(n)\) complexity.
200 Particle Filters
By Zachary Sunberg
