Neural Network Function Approximation
Do we really need to keep track of \(U(s)\) for every \(U\) separately?
Function Approximation
\(y \approx f_\theta(x)\)
Example: Linear Function Approximation:
\[f_\theta(x) = \theta^\top \beta(x)\]
e.g. \(\beta_i(x) = \sin(i \, \pi \, x)\)
AI = Neural Nets
Neural Nets are just another function approximator
Neural Network
\(h(x) = \sigma(Wx + b)\)
Neural Network
\(h(x) = \sigma(Wx + b)\)
Neural Network
\(h(x) = \sigma(Wx + b)\)
\(f_\theta(x) = h^{(2)}\left(h^{(1)}(x)\right)\)
\(= \sigma^{(2)}\left(W^{(2)} \sigma^{(1)}\left(W^{(1)} x + b^{(1)}\right) + b^{(2)}\right)\)
\(\theta = (W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)})\)
Nonlinearities
Training
\[\theta^* = \argmin_\theta \sum_{(x,y) \in \mathcal{D}} l(f_\theta(x), y)\]
Stochastic Gradient Descent: \(\theta \gets \theta - \alpha \, \nabla_\theta\, l (f_\theta(x), y)\)
Chain Rule
Chain Rule
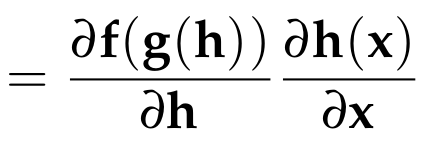
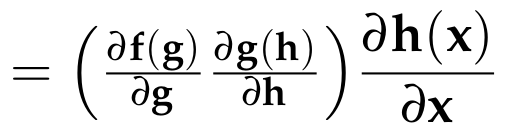
Example:
\[\hat{y} = W^{(2)} \sigma (W^{(1)} x + b^{(1)}) + b^{(2)}\]
\[\frac{\partial l}{\partial W^{(2)}} =\]
\[\frac{\partial l}{\partial \hat{y}} \left(\frac{\partial \hat{y}}{\partial W^{(2)}}\right)\]
\[ = \frac{\partial l}{\partial \hat{y}}\, \sigma\left(W^{(1)} x + b^{(1)}\right)^\top\]
\[W^{(2)} \gets W^{(2)} - \alpha \frac{\partial l}{\partial W^{(2)}}\]
(assume \(\hat{y}\) is scalar)
Automatic Differentiation
Backprop
\[l(x, y_\text{true}) = \left(\theta_2 x + \theta_1 - y_\text{true}\right)^2\]
a “fast and furious” approach to training neural networks does not work and only leads to suffering. Now, suffering is a perfectly natural part of getting a neural network to work well, but it can be mitigated by being thorough, defensive, paranoid, and obsessed with visualizations of basically every possible thing. The qualities that in my experience correlate most strongly to success in deep learning are patience and attention to detail.
- Andrej Karpathy
Adaptive Step Size: RMSProp
Adaptive Step Size: RMSProp
Adaptive Step Size: ADAM
(Adaptive Moment Estimation)
\(\odot\) means elementwise multiplication.
Adaptive Step Size: ADAM
Circle dot is elementwise product
On Your Radar: ConvNets
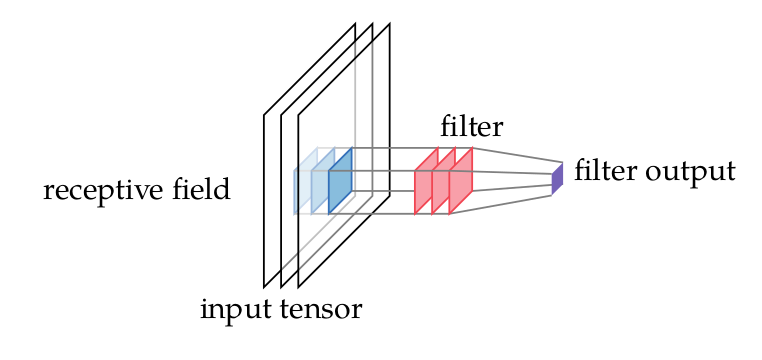
On Your Radar: Regularization
e.g. Batch norm, layer norm, dropout
On Your Radar: Skip Connections (Resnets)
Resources
OpenAI Spinning up
075 Neural Network Function Approximation
By Zachary Sunberg
