






A bit about me



Teaching is only half of my job...

Linux

Autonomous Decision and Control Laboratory

-
Algorithmic Contributions
- Scalable algorithms for partially observable Markov decision processes (POMDPs)
- Motion planning with safety guarantees
- Game theoretic algorithms
-
Theoretical Contributions
- Particle POMDP approximation bounds
-
Applications
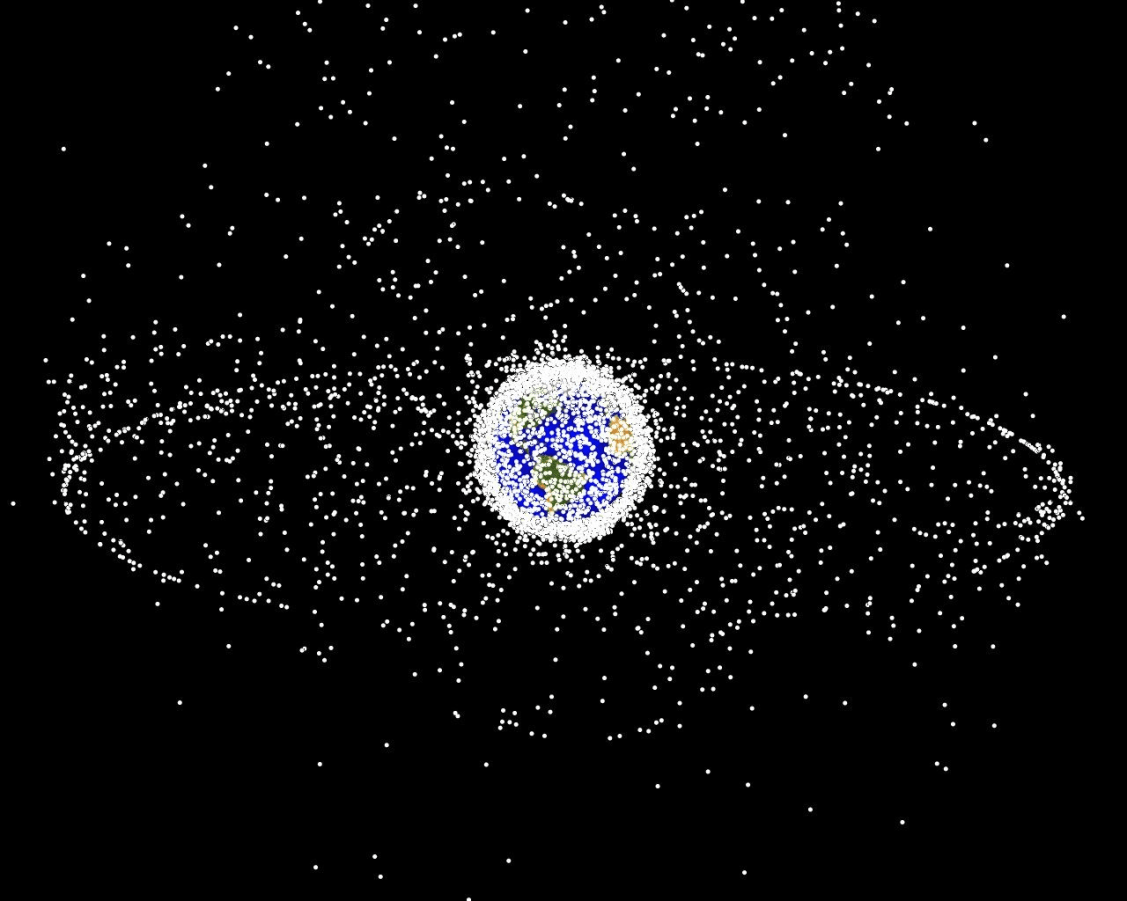
- Space Domain Awareness
- Autonomous Driving
- Autonomous Aerial Scientific Missions
- Search and Rescue
- Space Exploration
- Ecology
-
Open Source Software
- POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students









Postdoc



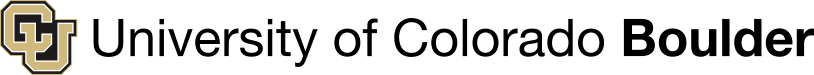


Tweet by Nitin Gupta
29 April 2018
https://twitter.com/nitguptaa/status/990683818825736192
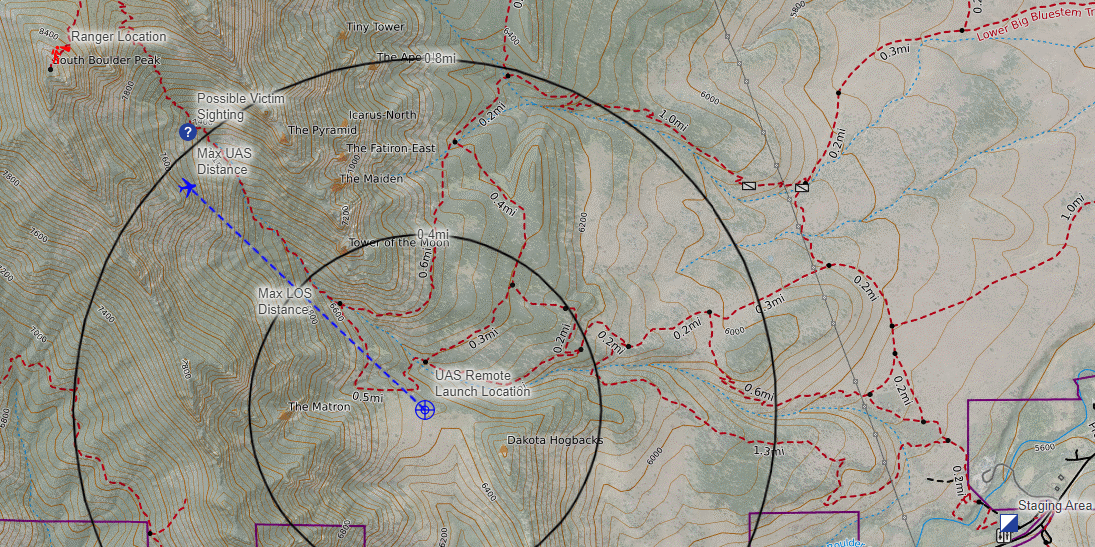
Example 1:
Autonomous Driving
Example 2: Tornados
Video: Eric Frew
Example 2: Tornados



Example 3: Search and Rescue


What do they have in common?
Driving: what are the other road users going to do?
Tornado Forecasting: what is going on in the storm?
Search and Rescue: where is the lost person?
All are sequential decision-making problems with uncertainty!
All can be modeled as a POMDP (with a very large state and observation spaces).



Markov Decision Process (MDP)
- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Aleatory

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)
\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)
\[\underset{\pi:\, \mathcal{S} \to \mathcal{A}}{\text{maximize}} \quad \text{E}\left[ \sum_{t=0}^\infty R(s_t, a_t) \right]\]
Reinforcement Learning
- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
Aleatory
Epistemic (Static)


\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)
\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)
Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
- \(\mathcal{O}\) - Observation space
- \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution
Aleatory
Epistemic (Static)
Epistemic (Dynamic)

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)
\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)
Solving a POMDP
Environment
Belief Updater
Planner
\(a = +10\)


True State
\(s = 7\)
Observation \(o = -0.21\)

\(b\)
\[b_t(s) = P\left(s_t = s \mid b_0, a_0, o_1 \ldots a_{t-1}, o_{t}\right)\]

\[ = P\left(s_t = s \mid b_{t-1}, a_{t-1}, o_{t}\right)\]
\(Q(b, a)\)
\(O(|\mathcal{S}|^2)\)
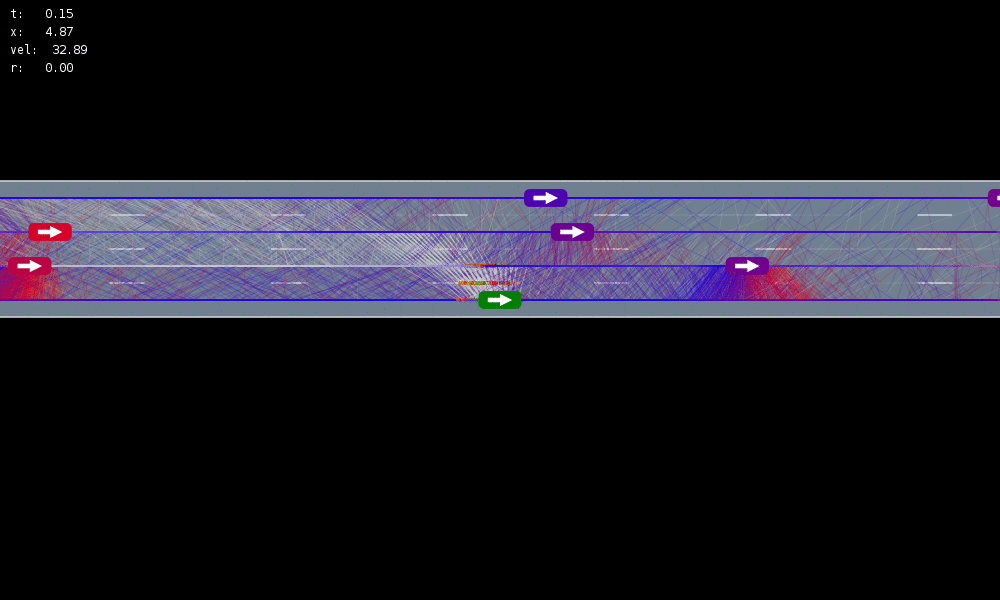
Navigation among Pedestrians
[Gupta, Hayes, & Sunberg, AAMAS 2022]
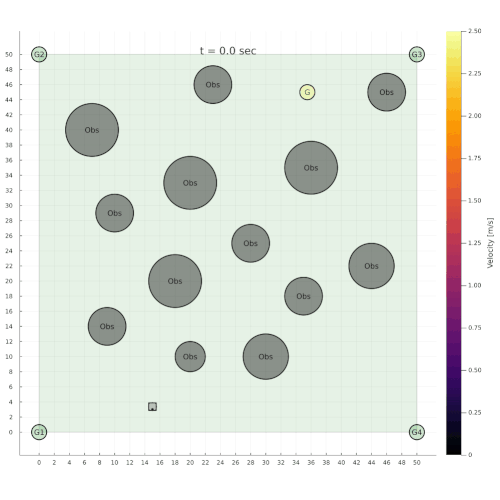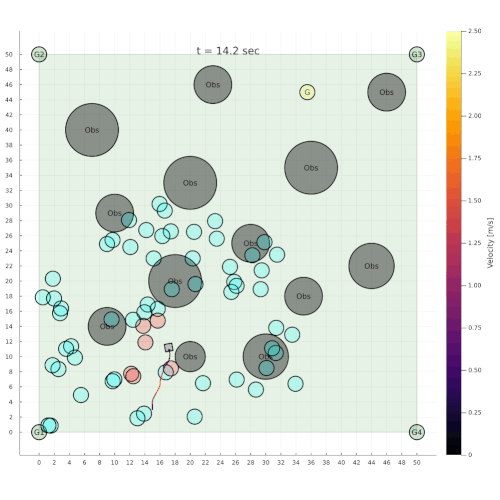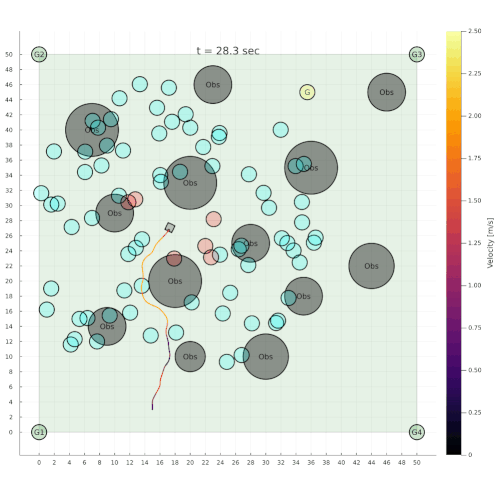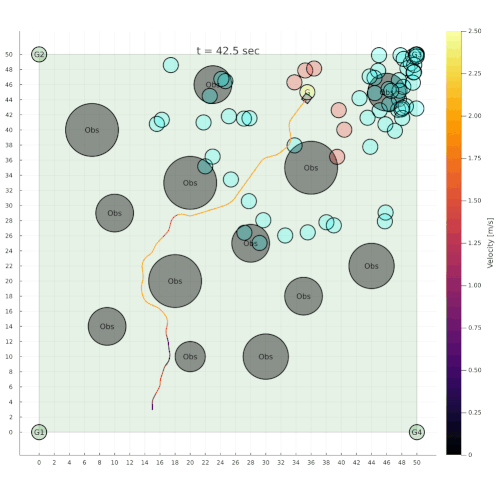


Previous solution: 1-D POMDP (92s avg)
Our solution (65s avg)
State:
- Vehicle physical state
- Human physical state
- Human intention

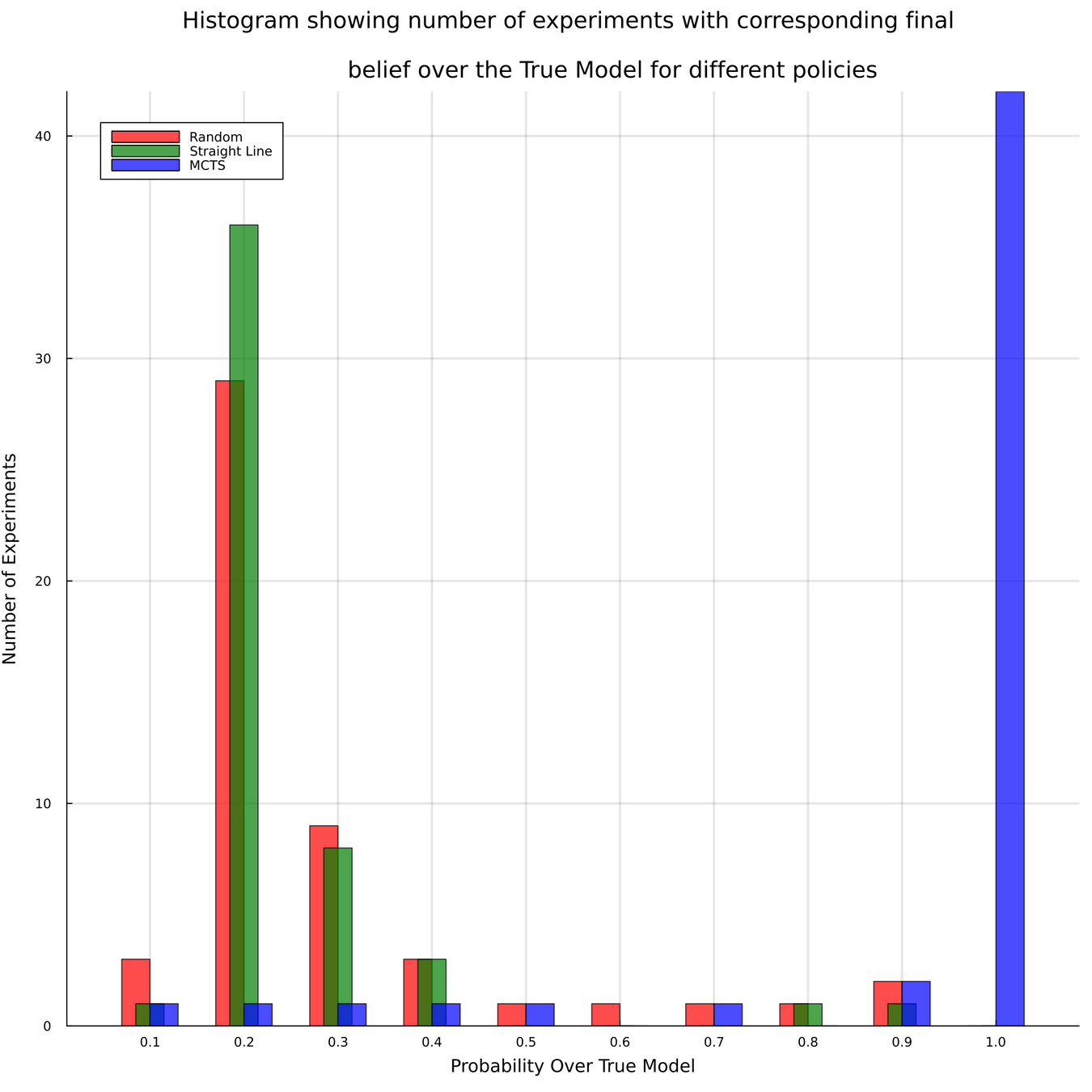
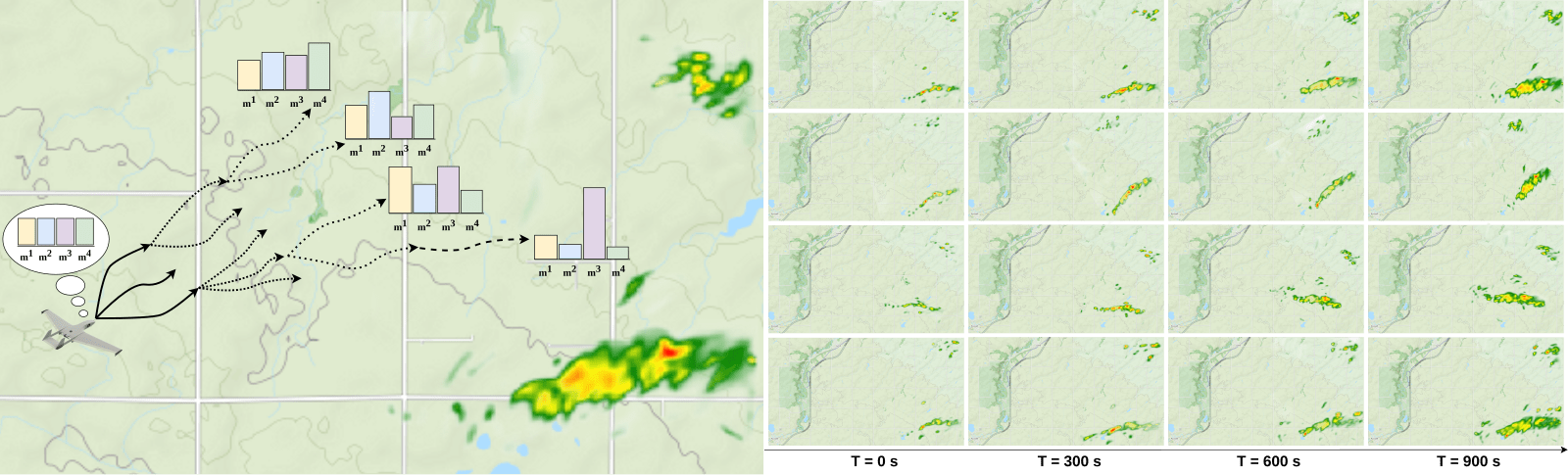
Meteorology
- State: (physical state of aircraft, which forecast is the truth)
- Action: (flight direction, drifter deploy)
- Reward: Terminal reward for correct weather prediction
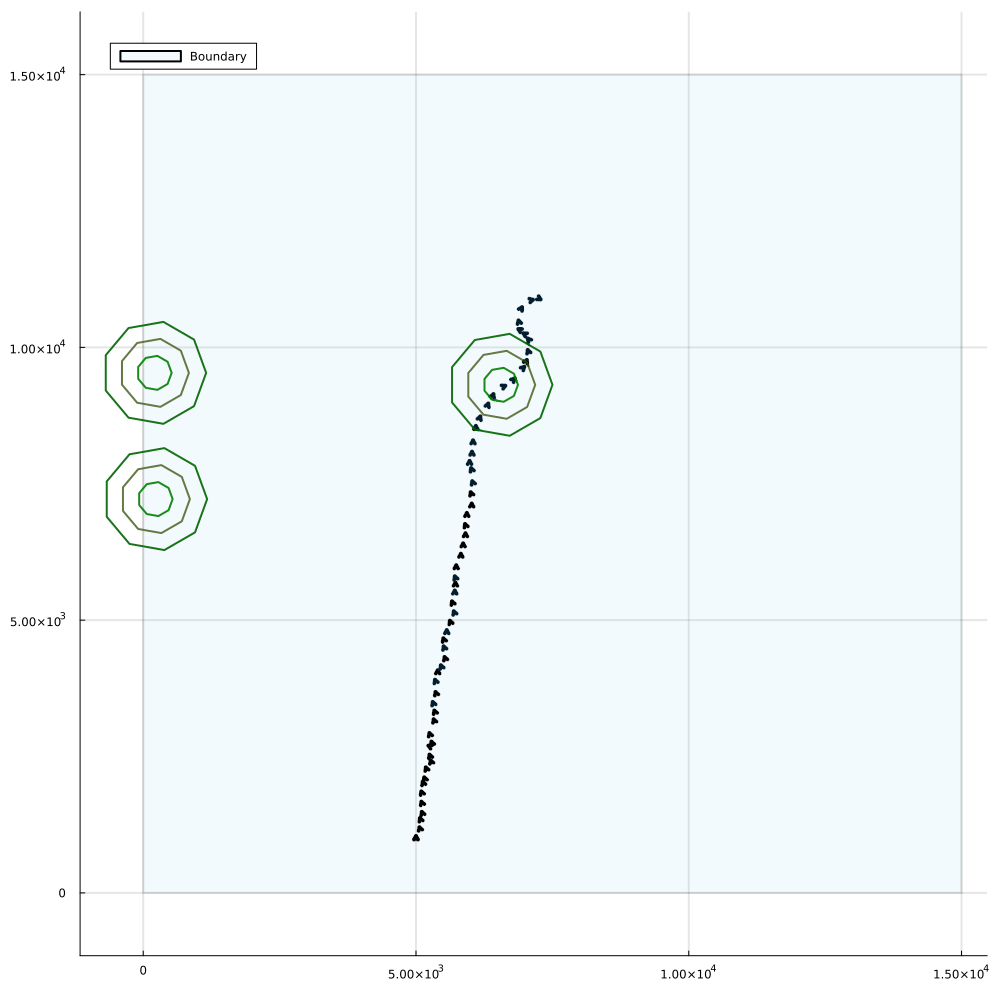

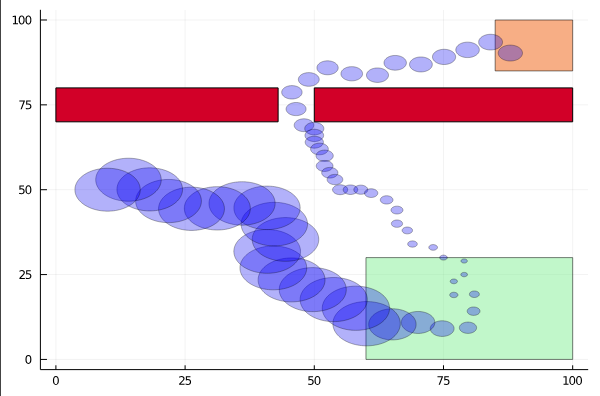
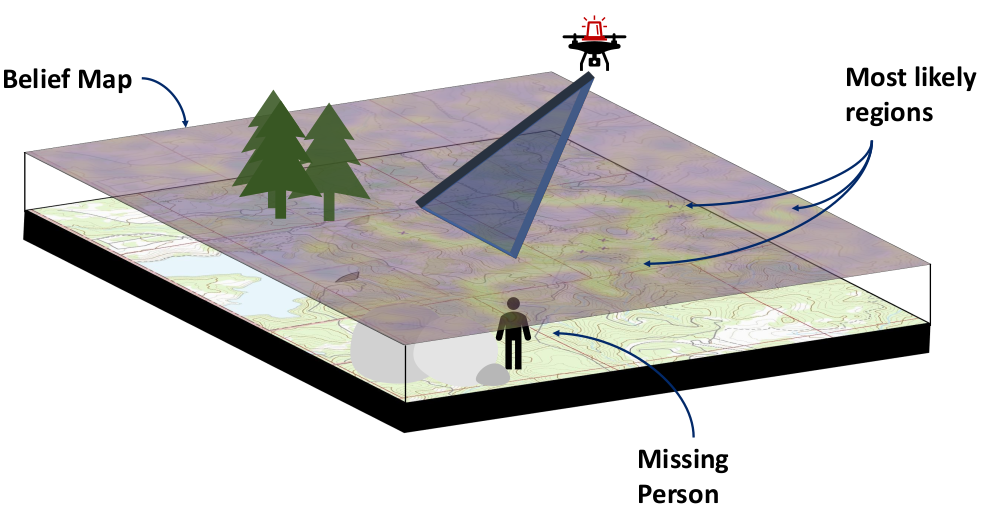
Drone Search and Rescue
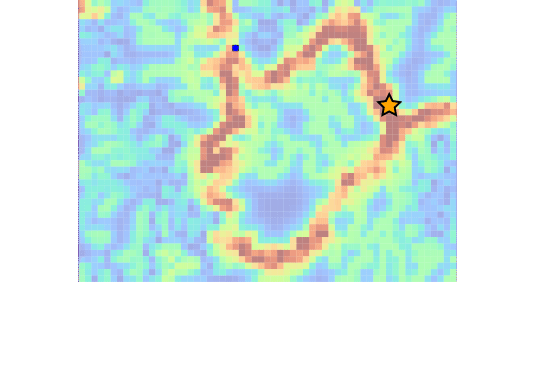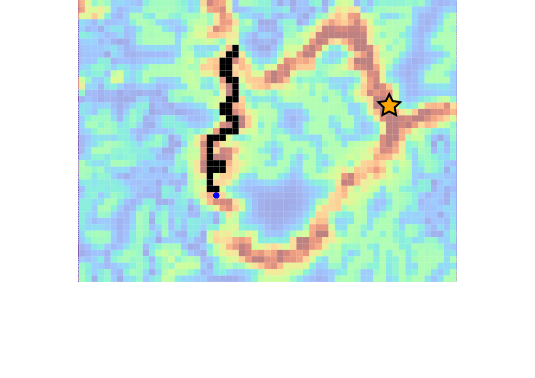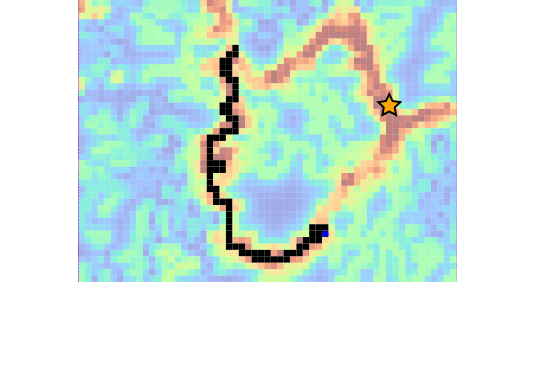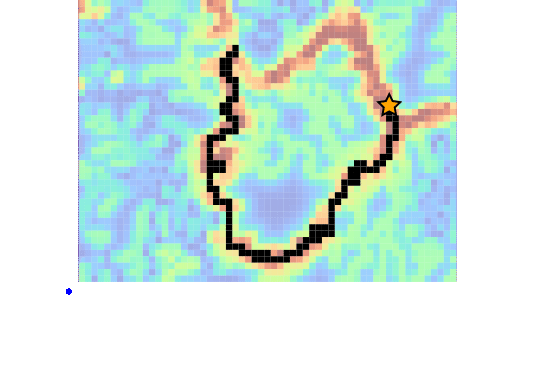
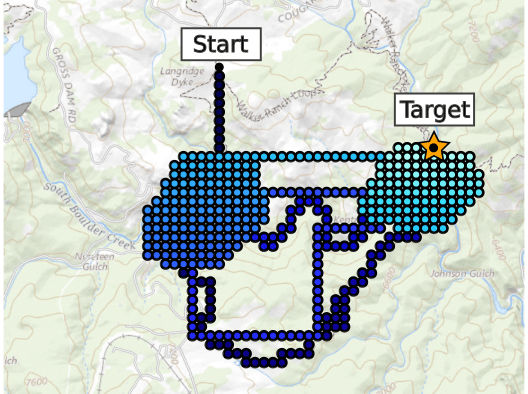




State:
- Location of Drone
- Location of Human
Baseline
Our POMDP Planner

[Ray, Laouar, Sunberg, & Ahmed, ICRA 2023]
Drone Search and Rescue
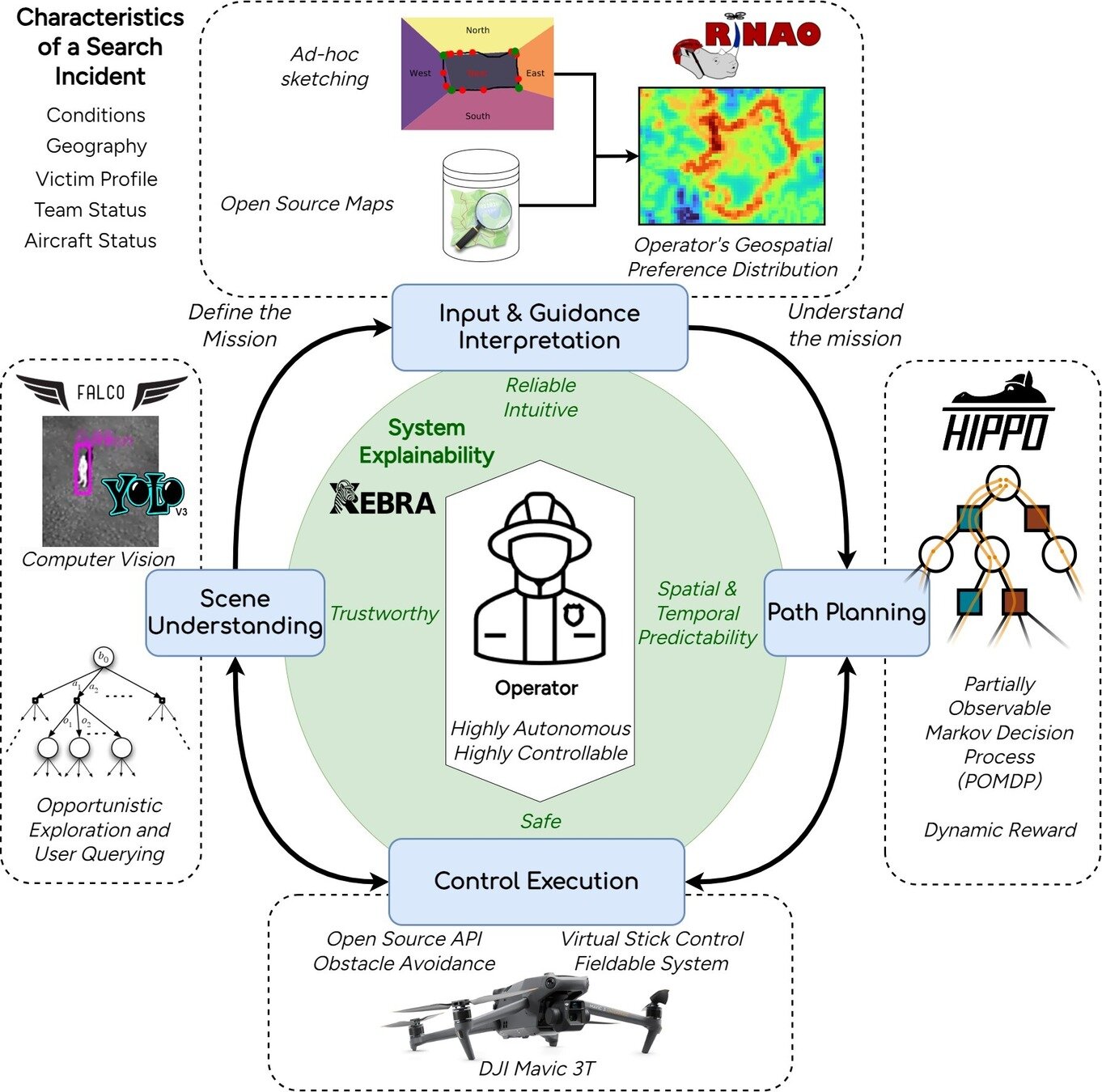





[Ray, Laouar, Sunberg, & Ahmed, ICRA 2023]
Space Domain Awareness

(Result for simplified dynamical system)

State:
- Position, velocity of object-of-interest
- Anomalies: navigation failure, suspicious maneuver, thruster failure, etc.
Innovation: Large language models allow analysts to quickly specify anomaly hypotheses
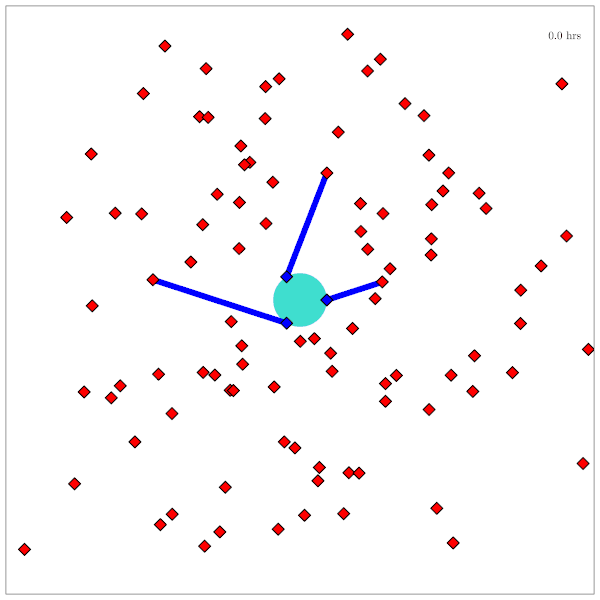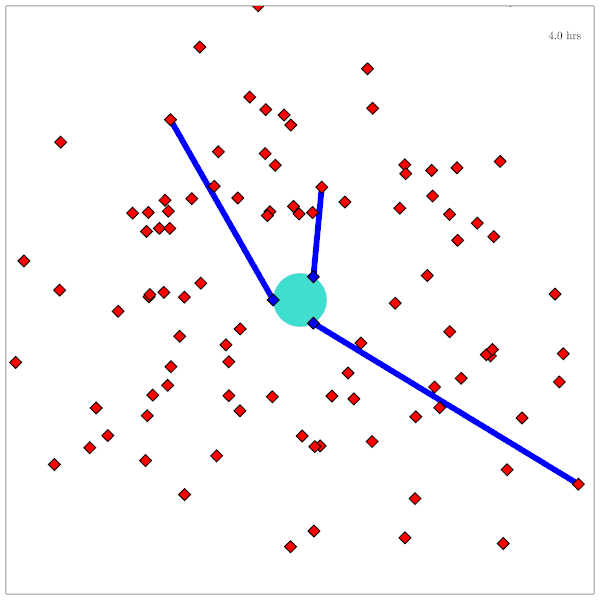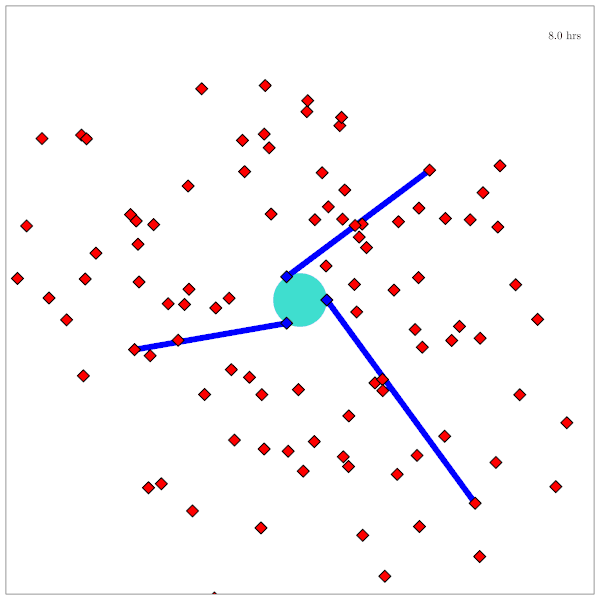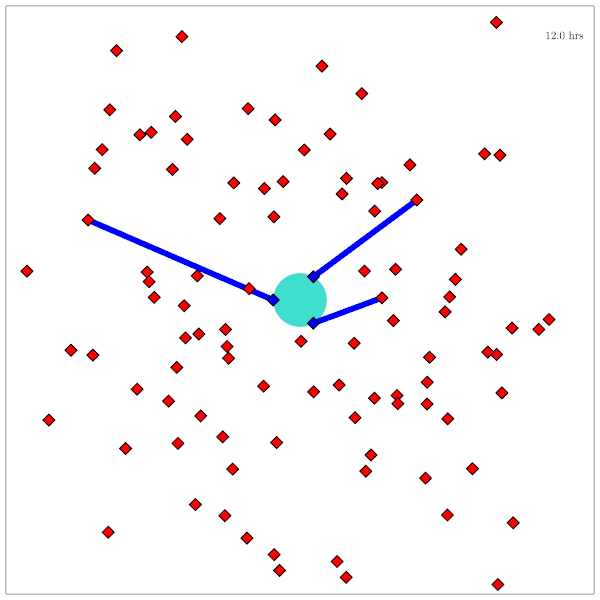
Catalog Maintenance Plan


Partially Observable Stochastic Game (POSG)
Aleatory
Epistemic (Static)
Epistemic (Dynamic)
Interaction
- \(\mathcal{S}\) - State space
- \(T(s' \mid s, \bm{a})\) - Transition probability distribution
- \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
- \(R^i(s, \bm{a})\) - Reward function (cooperative, opposing, or somewhere in between)
- \(\mathcal{O}^i, \, i \in 1..k\) - Observation spaces
- \(Z(o^i \mid \bm{a}, s')\) - Observation probability distributions

POSG Example: Missile Defense
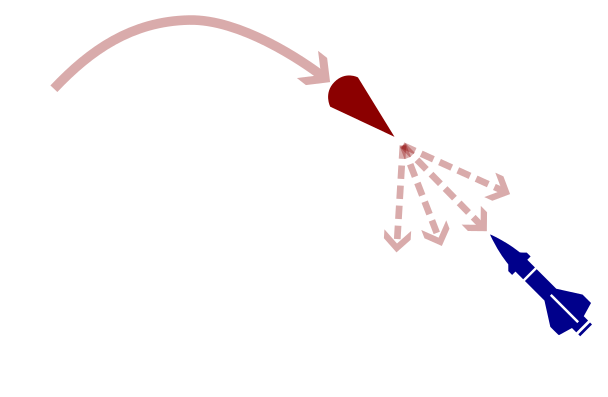
POMDP Solution:
- Assume a distribution for the missile's actions
- Update belief according to this distribution
- Use a POMDP planner to find the best defensive action
Nash equilibrium: All players play a best response to the other players
Fundamentally impossible for POMDP solvers to compute.
May include stochastic behavior (bluffing)
A shrewd missile operator will use different actions, invalidating our belief
Tree Search Algorithms for POSGs
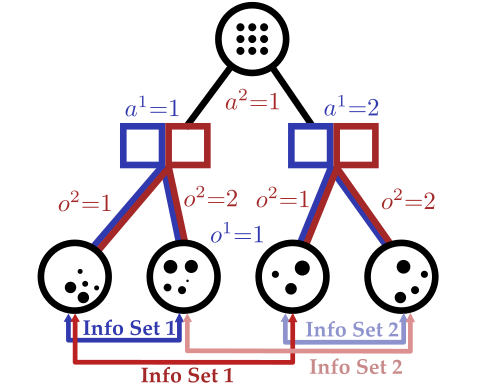
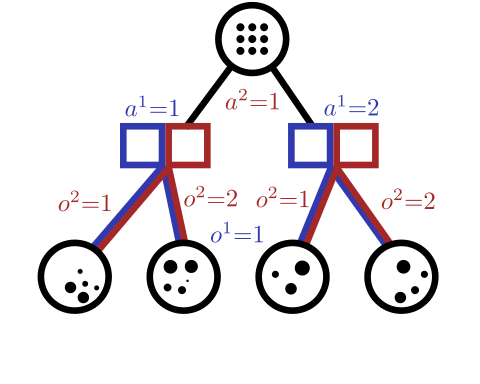
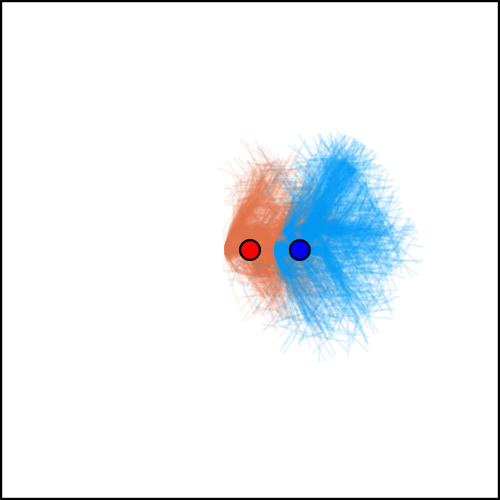
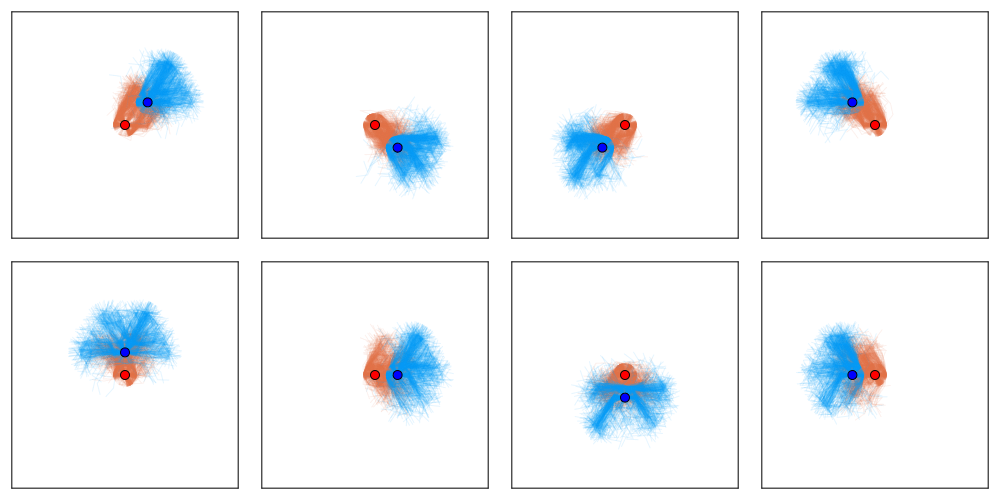
[Becker & Sunberg, NeurIPS 2024 (Under Review)]

Thank You!











Funding orgs: (all opinions are my own)






VADeR
006-A-Bit-About-Me
By Zachary Sunberg
006-A-Bit-About-Me
- 304



