Research Update
Tyler Becker
R^T_i(\sigma_i') = \sum_{t=1}^T \left[u(\sigma'_i,\sigma^t_{-i}) - u(\sigma^t_i,\sigma^t_{-i})\right]
Regret in not playing pure strategy \(\sigma'\), having instead played \(\sigma^t\)
Regret Matching
Decompose joint strategy \(\sigma\) into \(\sigma_i, \sigma_{-i} \)
R^T_i(\sigma_i') = \sum_{t=1}^T \left[u(\sigma'_i,\sigma^t_{-i}) - u(\sigma^t_i,\sigma^t_{-i})\right]
\sigma_{i}^{T+1}(\sigma')= \begin{cases}\frac{R_{i}^{T,+}(\sigma')}{\sum_{\sigma \in \Sigma_i} R_{i}^{T,+}(\sigma)} & \text { if } \sum_{\sigma \in \Sigma_i} R_{i}^{T,+}(\sigma)>0 \\ \frac{1}{|\Sigma_i|} & \text { otherwise. }\end{cases}
\bar{\sigma}_i = \frac{1}{T}\sum_{t=1}^T\sigma_i^t
Regret Matching
Finding Unexploitable Strategies
Finding maximally exploitative strategy with static opponent
Converging to unexploitable strategy via self-play
1
2
...
...
...
...
...
...
...
\(N\)
Ability to solve arbitrarily sized matrix games efficiently
\(\mathcal{A} = \mathbb{R}^{N\times N}\)
U(\vec{\sigma}) = \begin{bmatrix}
(10,-10) & (-1,1) & \dots & (-1,1)\\
(-1,1) & (10,-10) & & \vdots\\
\vdots & & \ddots & & \\
(-1,1) & \dots & \dots & (10,-10) \\
\end{bmatrix}
U(\vec{\sigma}) = \begin{bmatrix}
(10,-10) & (-1,1) & \dots & (-1,1)\\
(-1,1) & (10,-10) & & \vdots\\
\vdots & & \ddots & & \\
(-1,1) & \dots & \dots & (10,-10) \\
\end{bmatrix}
Static Opponent Strategy
U(\vec{\sigma}) = \begin{bmatrix}
(10,-10) & (-1,1) & \dots & (-1,1)\\
(-10,10) & (10,-10) & & \vdots\\
\vdots & & \ddots & & \\
(-10,10) & \dots & \dots & (10,-10) \\
\end{bmatrix}
Non-uniform Equilibria
Extensive Form Games
- Reasoning about action histories
R
P
S
Player 1
Player 2
\sigma : H \rightarrow \mathcal{A}
R
P
S
R
P
S
R
P
S
R
P
S
Player 1
Player 2
(0,0)
(0,0)
(0,0)
(-1,1)
(-1,1)
(-1,1)
(1,-1)
(1,-1)
(1,-1)
\sigma : H \rightarrow \mathcal{A}
Extensive Form Games
- Reasoning about action histories
Imperfect Information Extensive Form Games
- Reasoning about information sets
R
P
S
R
P
S
R
P
S
R
P
S
Player 1
Player 2
(0,0)
(0,0)
(0,0)
(-1,1)
(-1,1)
(-1,1)
(1,-1)
(1,-1)
(1,-1)
I_1
I_2
\sigma : \mathcal{I} \rightarrow \mathcal{A}
Counterfactual Regret Minimization
R_{i}^{T}(I, a)=\frac{1}{T} \sum_{t=1}^{T} \pi_{-i}^{\sigma^{t}}(I)\left(u_{i}\left(\left.\sigma^{t}\right|_{I \rightarrow a}, I\right)-u_{i}\left(\sigma^{t}, I\right)\right)
u_{i}(\sigma, I)=\frac{\sum_{h \in I, h^{\prime} \in Z} \pi_{-i}^{\sigma}(h) \pi^{\sigma}\left(h, h^{\prime}\right) u_{i}\left(h^{\prime}\right)}{\pi_{-i}^{\sigma}(I)}
Counterfactual Regret Minimization
\sigma_{i}^{T+1}(I)(a)= \begin{cases}\frac{R_{i}^{T,+}(I, a)}{\sum_{a \in A(I)} R_{i}^{T,+}(I, a)} & \text { if } \sum_{a \in A(I)} R_{i}^{T,+}(I, a)>0 \\ \frac{1}{|A(I)|} & \text { otherwise. }\end{cases}
\bar{\sigma}_{i}^{t}(I)(a)=\frac{\sum_{t=1}^{T} \pi_{i}^{\sigma^{t}}(I) \sigma^{t}(I)(a)}{\sum_{t=1}^{T} \pi_{i}^{\sigma^{t}}(I)}
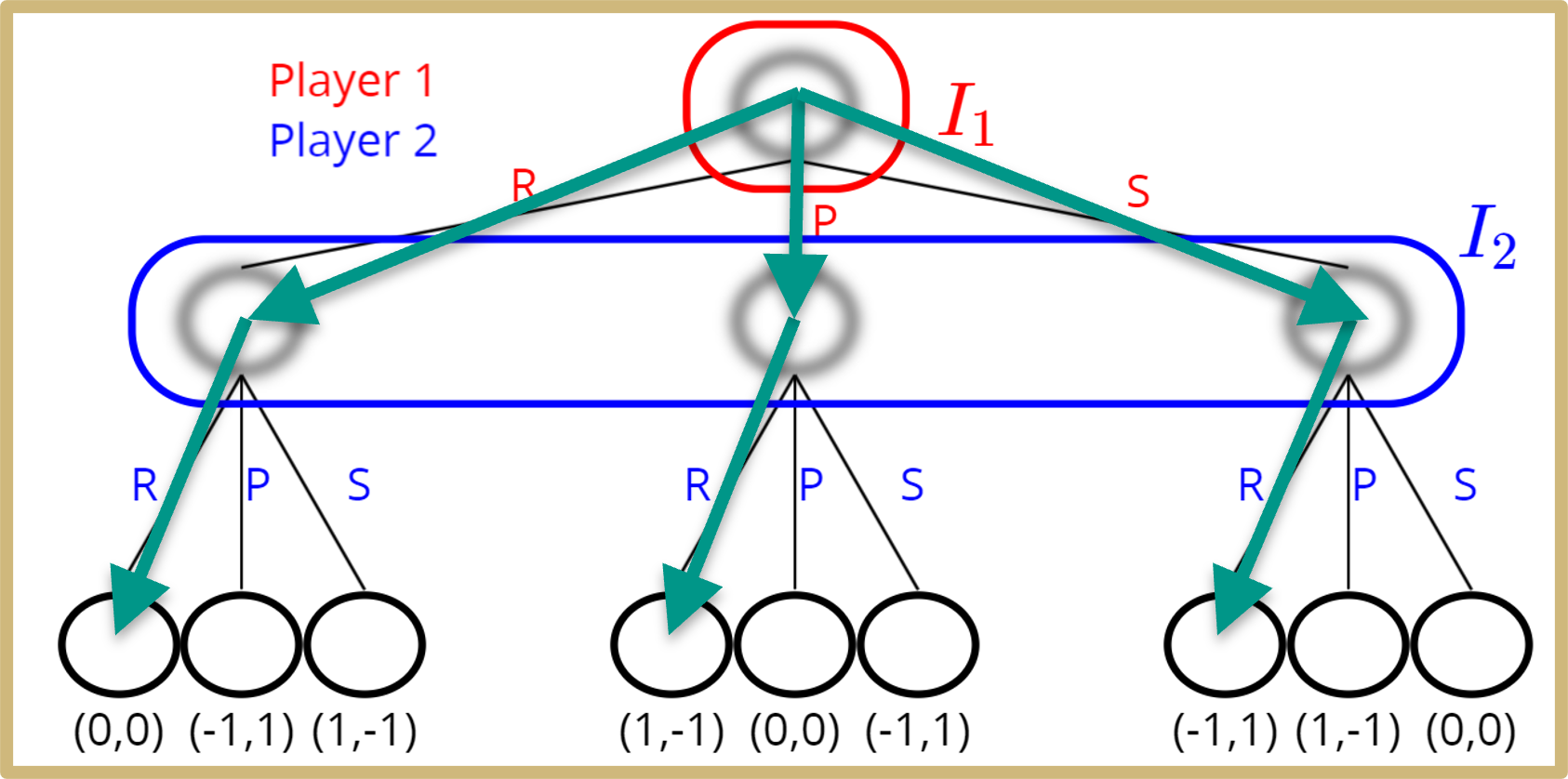
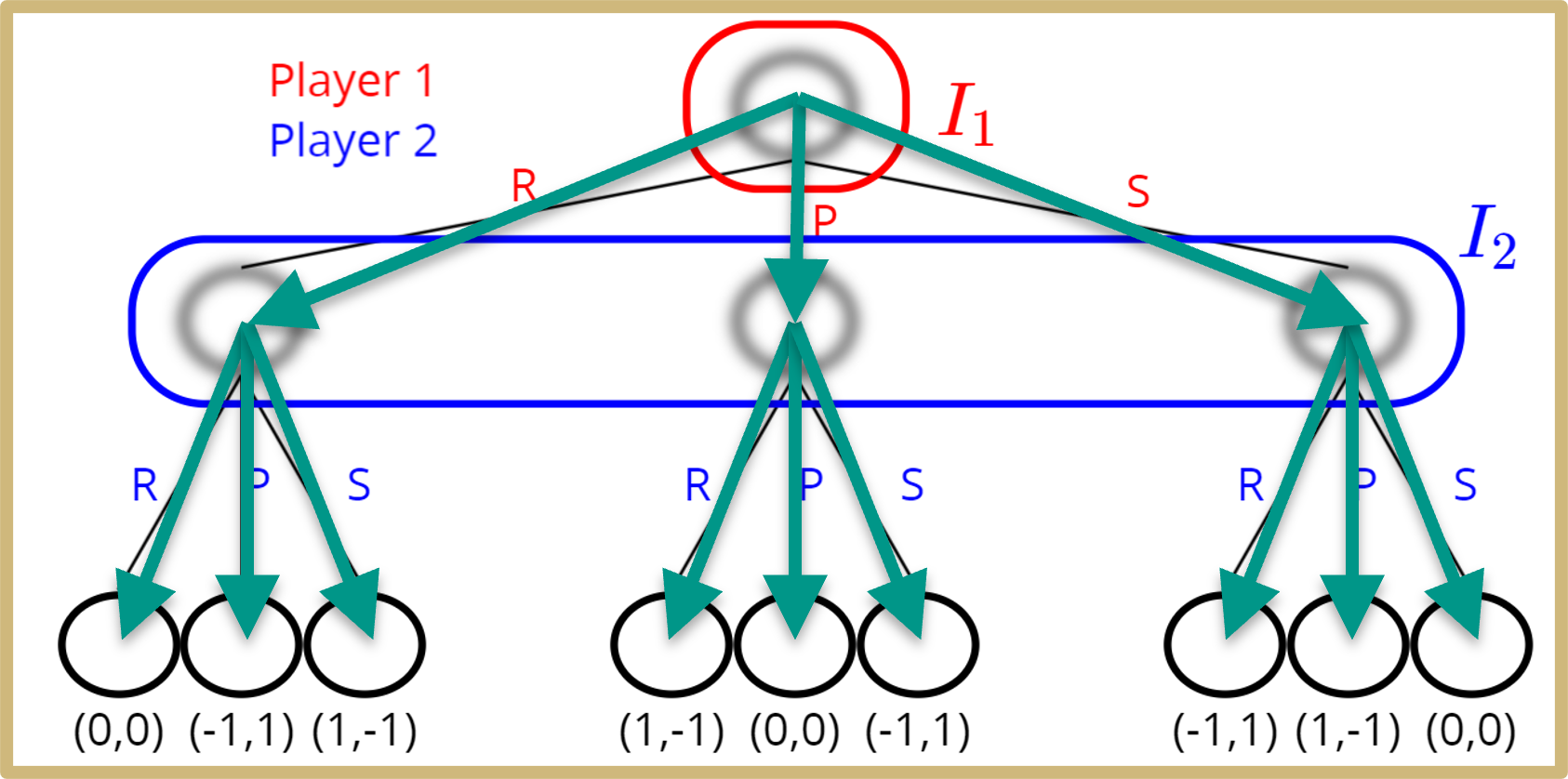
Vanilla CFR
(ES)MCCFR
Exhaustive Tree Search
- Search time exponential in search horizon
- Long convergence time for long planning horizon problems
Sparse Tree Search
- Faster search/convergence time
- Allows sampling from opponent strategy to find maximally exploitative counter-strategy (data-driven)
1
2
...
...
...
...
...
...
...
\(N\)
\tilde{v}_{i}(\sigma, I \mid j)=\sum_{z \in Q_{j} \cap Z_{I}} \frac{1}{q(z)} u_{i}(z) \pi_{-i}^{\sigma}(z[I]) \pi^{\sigma}(z[I], z)
r^t(I,a) = v^{\sigma^t}(I,a) - v^{\sigma^t}(I)
(I,r,t)
(I,\sigma^t,t)
Deep CFR
I
r(I,a_1)
r(I,a_2)
I
\sigma(I,a_1)
\sigma(I,a_2)
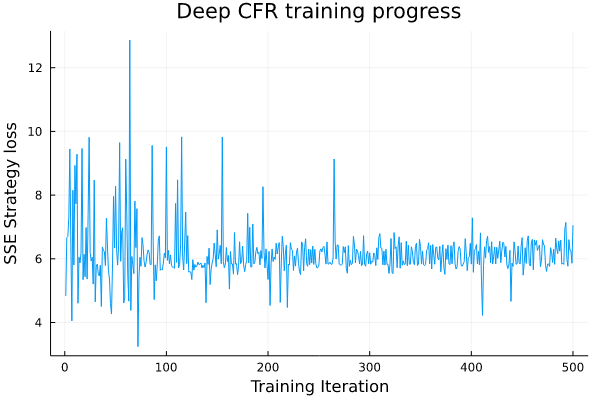
Deep CFR
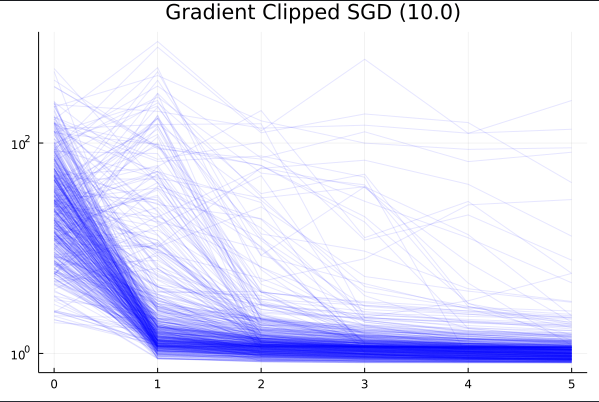
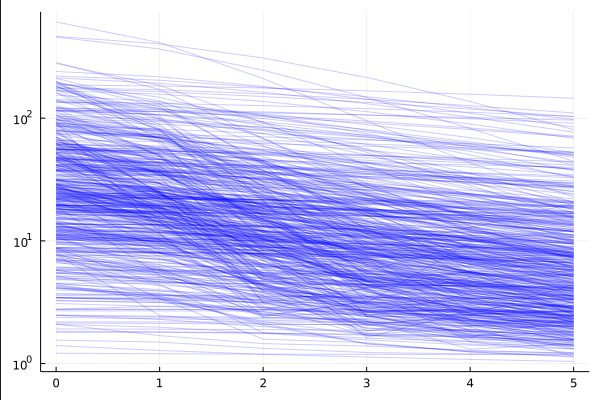
ADAM (0.01)
CFR Research Update
By Tyler Becker
