Stochastic Dynamic Games in Belief Space
Wilko Schwarting, Alyssa Pierson, Sertac Karaman, Daniella Rus
LQR
iLQR
iterative LQ Games
iLQG
Belief Space iLQG
Belief Space Dynamic Games
\dot{x} = Ax + Bu
J=\int_{0}^{\infty}\left(x^{T} Q x+u^{T} R u+2 x^{T} N u\right) d t
\dot{x} = f(x,u)
\dot{x} = f(x,u,m)
\dot{x} = f(x,u,m)
y = h(x,u,n)
Preliminaries
\(N\) agents \(\{1,\dots,N\}\)
Joint State: \(x_k \in R^{n_{x}}\)
Joint Action: \(u_k \in R^{n_{u}}\)
Joint Measurement: \(z_k \in R^{n_{z}}\)
Belief Dynamics
b_{k+1} = \beta(b_k, u_k, z_{k+1})
b' = \tau(b,a,o)
analogous to
Belief Update
\mathbf{b}\left(\mathbf{x}_{k+1}\right)=\eta p\left(\mathbf{z}_{k+1} \mid \mathbf{x}_{k+1}\right) \int p\left(\mathbf{x}_{k+1} \mid \mathbf{x}_{k}, \mathbf{u}_{k}\right) \mathbf{b}\left(\mathbf{x}_{k}\right) \mathrm{d} \mathbf{x}_{k}
Analytical Bayes filter solution intractable
\begin{aligned}\mathbf{x}_{k+1} &=f\left(\mathbf{x}_{k}, \mathbf{u}_{k}, \mathbf{m}_{k}\right), & \mathbf{m}_{k} & \sim \mathcal{N}(0, I) \\\mathbf{z}_{k} &=h\left(\mathbf{x}_{k}, \mathbf{n}_{k}\right) & \mathbf{n}_{k} & \sim \mathcal{N}(0, I)\end{aligned}
Resort to EKF
\begin{aligned}\hat{\mathbf{x}}_{k+1} &=f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right)+K_{k}\left(\mathbf{z}_{k+1}-h\left(f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right), 0\right)\right) \\\Sigma_{k+1} &=\Gamma_{k+1}-K_{k} H_{k} \Gamma_{k+1}\end{aligned}
Belief Update
\begin{aligned}\mathbf{x}_{k+1} &=f\left(\mathbf{x}_{k}, \mathbf{u}_{k}, \mathbf{m}_{k}\right), & \mathbf{m}_{k} & \sim \mathcal{N}(0, I) \\\mathbf{z}_{k} &=h\left(\mathbf{x}_{k}, \mathbf{n}_{k}\right) & \mathbf{n}_{k} & \sim \mathcal{N}(0, I)\end{aligned}
\begin{aligned}\hat{\mathbf{x}}_{k+1} &=f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right)+K_{k}\left(\mathbf{z}_{k+1}-h\left(f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right), 0\right)\right) \\\Sigma_{k+1} &=\Gamma_{k+1}-K_{k} H_{k} \Gamma_{k+1}\end{aligned}
\begin{aligned}\Gamma_{k+1} &=A_{k} \Sigma_{k} A_{k}^{T}+M_{k} M_{k}^{T} \\K_{k} &=\Gamma_{k+1} H_{k}^{\top}\left(H_{k} \Gamma_{k+1} H_{k}^{\top}+N_{k} N_{k}^{\top}\right)^{-1} \\A_{k} &=\frac{\partial f}{\partial \mathbf{x}}\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right), \quad M_{k}=\frac{\partial f}{\partial \mathbf{m}}\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right) \\H_{k} &=\frac{\partial h}{\partial \mathbf{x}}\left(f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right), 0\right), \quad N_{k}=\frac{\partial h}{\partial \mathbf{n}}\left(f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right), 0\right)\end{aligned}
\begin{aligned}
\Sigma_{k+1} &= P_k^+ \\
\Gamma_{k+1} &= P_k^- \\
A_k &= F_k \\
M_kM_k^T &= Q \\
N_kN_k^T &= R \\
\end{aligned}
Their Notation
Our Notation
Belief Update
g_{k}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right)=\left[\begin{array}{c}f\left(\hat{\mathbf{x}}_{k}, \mathbf{u}_{k}, 0\right) \\\operatorname{vec}\left(\Gamma_{k+1}-K_{k} H_{k} \Gamma_{k+1}\right)\end{array}\right]
\mathbf{b}_{k+1}=g\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right)+W\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right) \xi_{k}, \quad \xi_{k} \sim \mathcal{N}(0, I)
\(\xi_k\) accounts for both measurement and transition noise
W_{k}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right)=\left[\begin{array}{c}\sqrt{K_{k} H_{k} \Gamma_{k+1}} \\\mathbf{0}\end{array}\right]
Vectorize belief:
\mathbf{b}_k = [\hat{x}_k^T, \text{vec}(\Sigma_k)^T]^T
POMDP Best Response Game
Q^i(b_0, u) = \mathbb{E}_{z}\left[c_l^i(b_l) + \sum_{k=0}^{l-1}c_k^i(b_k,u_k)\right]
Expected Return for agent \(i\)
\(c_l\) - cost at final time-step (terminal cost)
\(c_k\) - cost for any intermediary time step
\pi^{i}=\underset{\mathbf{u}^{i}}{\arg \min } Q^{i}\left(\mathbf{b}_{0}, \mathbf{u}\right) \quad \forall i \in\{1, \ldots, N\} \\
\text { s.t. } \mathbf{b}_{k+1}=\beta\left(\mathbf{b}_{k}, \mathbf{u}_{k}, \mathbf{z}_{k+1}\right)
\begin{aligned}V_{l}^{i}\left(\mathbf{b}_{l}\right) &=c_{l}^{i}\left(\mathbf{b}_{l}\right) \\Q_{k}^{i}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right) &=c_{k}^{i}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right)+\underset{\mathbf{z}_{k+1}}{\mathbb{E}}\left[V_{k+1}^{i}\left(\beta\left(\mathbf{b}_{k}, \mathbf{u}_{k}, \mathbf{z}_{k+1}\right)\right)\right] \\V_{k}^{i}\left(\mathbf{b}_{k}\right) &=\min _{\mathbf{u}_{k}^{i}} Q_{k}^{i}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right) \\\pi_{k}^{i}\left(\mathbf{b}_{k}\right) &=\underset{\mathbf{u}_{k}^{i}}{\arg \min } Q_{k}^{i}\left(\mathbf{b}_{k}, \mathbf{u}_{k}\right)\end{aligned}
((\(\pi^i\) is a function of \(\pi^{\neg i}\)))
Iterative Dynamic Programming
Necessary condition of local Nash Equilibrium:
\frac{\partial Q_k^i(b_k,u_k)}{\partial u_k^i} = 0 \quad \forall i \in \{1,\dots, N\}
Optimize over perturbations
\begin{aligned}
\bar{b} &= b - \delta b \\
\bar{u} &= u - \delta u \\
\bar{s} &= s - \delta s \quad (\bar{s} = \left[\bar{b}^T, \bar{u}^T\right]^T)
\end{aligned}
V_{k}^{i}\left(\overline{\mathbf{b}}_{k}+\delta \mathbf{b}_{k}\right) \approx V_{k}^{i}+V_{\mathbf{b}, k}^{i, \top} \delta \mathbf{b}_{k}+\frac{1}{2} \delta \mathbf{b}_{k}^{\top} V_{\mathbf{b b}, k}^{i} \delta \mathbf{b}_{k}
Quadratic Value Approximation
\left( f(x) \approx f(a) + f'(a)(x-a) + \frac{1}{2}f''(a)(x-a)^2 \right)
Q_{k}^{i}\left(\overline{\mathbf{s}}_{k}+\delta \mathbf{s}_{k}\right) \approx Q_{k}^{i}+Q_{\mathrm{s}, k}^{i, \top} \delta \mathbf{s}_{k}+\frac{1}{2} \delta \mathbf{s}_{k}^{\top} Q_{\mathrm{ss}, k}^{i} \delta \mathbf{s}_{k}
\delta \mathbf{u}_{k}^{i, *}=\underset{\delta \mathbf{u}_{k}^{i}}{\arg \min }\left\{Q_{\mathbf{s}, k}^{i, \top} \delta \mathbf{s}_{k}+\frac{1}{2} \delta \mathbf{s}_{k}^{\top} Q_{\mathrm{ss}, k}^{i} \delta \mathbf{s}_{k}\right\}
\delta \mathbf{u}_{k}^{*}=-\hat{Q}_{\mathbf{u u}}^{-1}\left(\hat{Q}_{\mathbf{u}}+\hat{Q}_{\mathbf{u b}} \delta \mathbf{b}_{k}\right)
\hat{Q}_{\mathrm{uu}}=\left[\begin{array}{c}Q_{\mathrm{u}^{1}}^{1} \mathrm{u} \\Q_{\mathrm{u}^{2}}^{2} \mathrm{u} \\\vdots \\Q_{\mathrm{u}^{N}}^{N}\end{array}\right], \hat{Q}_{\mathrm{ub}}=\left[\begin{array}{c}Q_{\mathrm{u}^{1}}^{1} \mathrm{~b} \\Q_{\mathrm{u}^{2} \mathrm{~b}}^{2} \\\vdots \\Q_{\mathrm{u}^{N} \mathrm{~b}}^{N}\end{array}\right], \hat{Q}_{\mathrm{u}}=\left[\begin{array}{c}Q_{\mathrm{u}^{1}}^{1} \\Q_{\mathrm{u}^{2}}^{2} \\\vdots \\Q_{\mathrm{u}^{N}}^{N}\end{array}\right]
\pi_k = \bar{\mathbf{u}}_k + j_k + K_k\delta\mathbf{b}_k
j_k = \hat{Q}_{\mathbf{u}\mathbf{u}}^{-1}\hat{Q}_{\mathbf{u}}
K_k = -\hat{Q}_{\mathbf{u}\mathbf{u}}^{-1}\hat{Q}_{\mathbf{u}\mathbf{b}}
Nominal
Feed-forward
Feedback
Backward Pass
V_{l}^{i}=c_{l}^{i}\left(\overline{\mathbf{b}}_{l}\right), \quad V_{\mathrm{b}, l}^{i}=\left.\frac{\partial c_{l}^{i}(\mathbf{b})}{\partial \mathbf{b}}\right|_{\mathrm{b}=\overline{\mathbf{b}}_{l}}, \quad V_{\mathrm{bb}, l}^{i}=\left.\frac{\partial^{2} c_{l}^{i}(\mathbf{b})}{\partial \mathbf{b}^{2}}\right|_{\mathrm{b}=\overline{\mathbf{b}}_{l}}
K_k = -\hat{Q}_{\mathbf{u}\mathbf{u}}^{-1}\hat{Q}_{\mathbf{u}\mathbf{b}}, \quad
j_k = \hat{Q}_{\mathbf{u}\mathbf{u}}^{-1}\hat{Q}_{\mathbf{u}}, \quad
\pi_k = \bar{\mathbf{u}}_k + j_k + K_k\delta\mathbf{b}_k
\hat{Q}_{\mathbf{u u}}=\left[\begin{array}{c}Q_{\mathbf{u}^{1} \mathbf{u}}^{1} \\Q_{\mathbf{u}^{2} \mathbf{u}}^{2} \\\vdots \\Q_{\mathbf{u}^{N} \mathbf{u}}^{N}\end{array}\right], \hat{Q}_{\mathbf{u b}}=\left[\begin{array}{c}Q_{\mathbf{u}^{1} \mathbf{b}}^{1} \\Q_{\mathbf{u}^{2} \mathbf{b}}^{2} \\\vdots \\Q_{\mathbf{u}^{N} \mathbf{b}}^{N}\end{array}\right], \hat{Q}_{\mathbf{u}}=\left[\begin{array}{c}Q_{\mathbf{u}^{1}}^{1} \\Q_{\mathbf{u}^{2}}^{2} \\\vdots \\Q_{\mathbf{u}^{N}}^{N}\end{array}\right]
Forward Pass
\tilde{Q}_{\mathbf{u}\mathbf{u}}^i = \hat{Q}_{\mathbf{u}\mathbf{u}}^i + \mu_{\mathbf{u}}I
\begin{aligned}\tilde{Q}_{\mathrm{ss}, k}^{i}=& c_{\mathrm{ss}, k}^{i}+g_{\mathrm{s}, k}^{T}\left(V_{\mathrm{bb}, k+1}^{i}+\mu_{\mathrm{b}} I\right) g_{\mathrm{s}, k} \\&+\sum_{i=1}^{n} W_{\mathrm{s}, k}^{(j), T}\left(V_{\mathrm{bb}, k+1}^{i}+\mu_{\mathrm{b}} I\right) W_{\mathrm{s}, k}^{(j)}\end{aligned}
Control Regularization
Belief Regularization
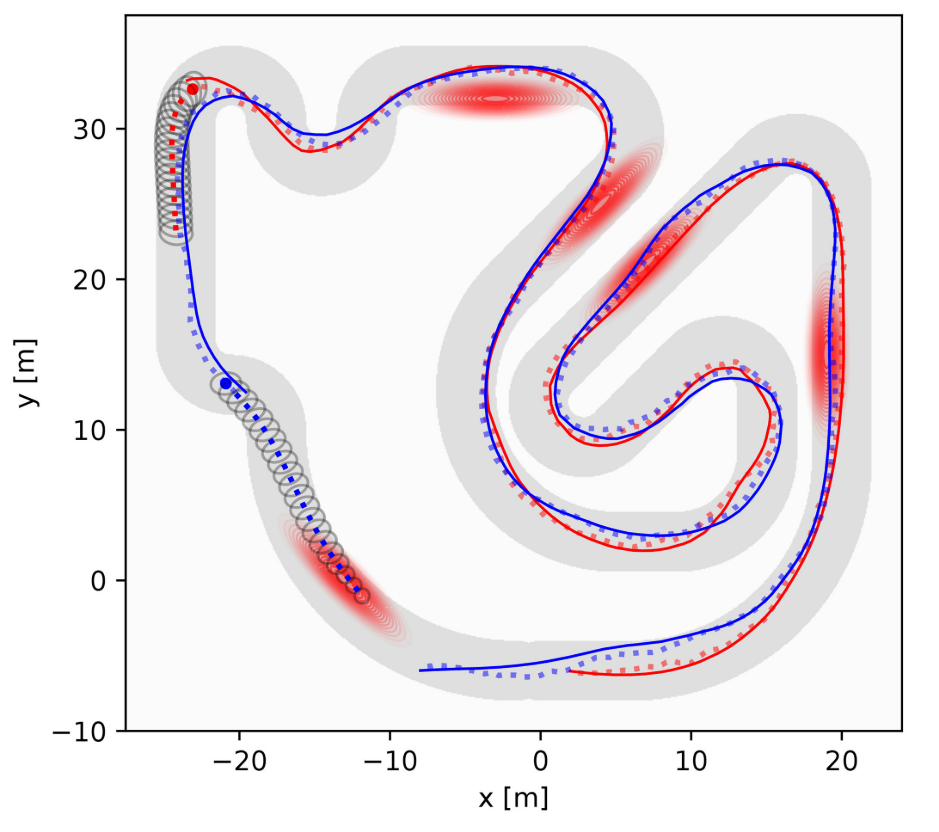
Experimental Results
Active Surveillance
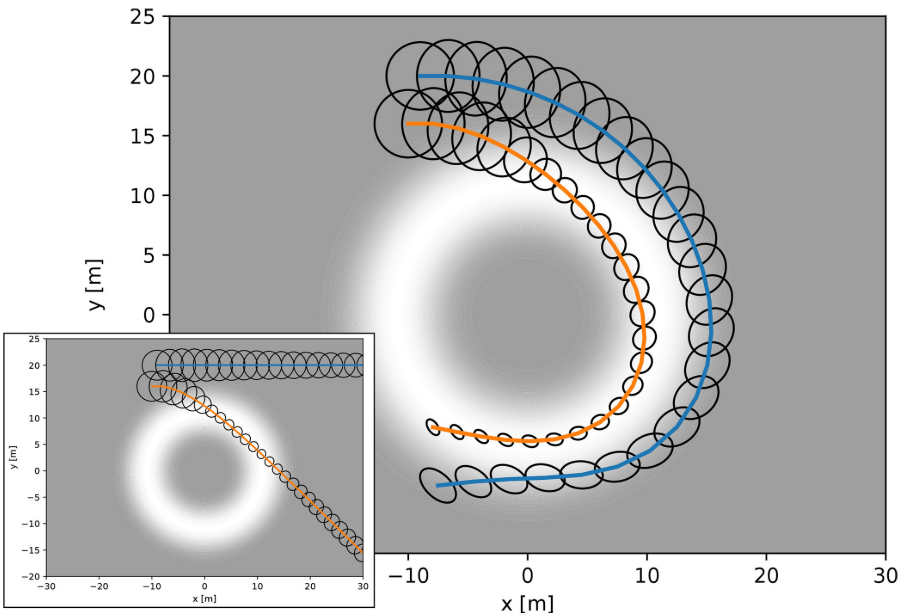
Agent 1 - observe agent 2
Agent 2 - maintain constant speed
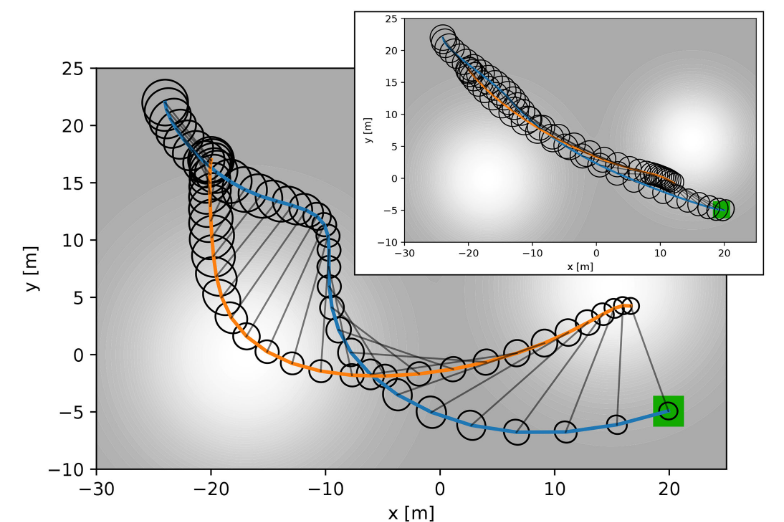
Experimental Results
Guide Dog for Blind Agent
Agent 1 - Guide agent 2 to goal with low unceratainty
Agent 2 - No navigational control
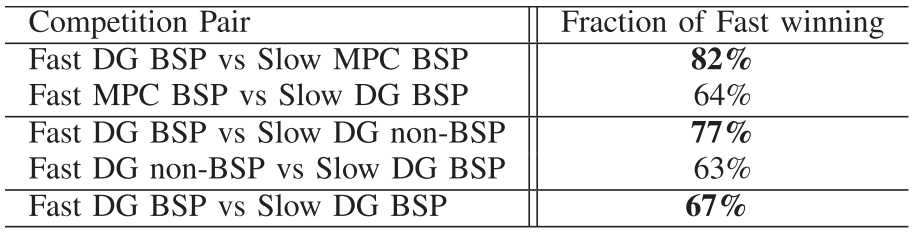
Experimental Results
Competitive Racing
Agent 1 - Faster than agent 2 but starts behind agent 2
Agent 2 - Slower than agent 1 but starts ahead
Stochastic Dynamic Games in Belief Space
By Tyler Becker
