Intention-Aware Navigation in Crowds with Extended-Space POMDP Planning
Himanshu Gupta


Bradley Hayes
Zachary Sunberg




Autonomous systems in the real world


A capable robot must
Infer pedestrian's intention
Predict pedestrian's behavior given its intention
Plan a path
to its goal location
Prior Work
Reactive Controller
Predict and Act Controller


Issues
- Pedestrian Model?
- Future effect of immediate actions?
Issue
- Uncertainty in pedestrian intention estimation?



Need a method that determines the optimal action for the vehicle at any given time by reasoning over the uncertainty in pedestrian intention estimation?

Need a method that determines the optimal action for the vehicle at any given time by reasoning over the uncertainty in pedestrian intention estimation?



Two-step Approach

Bai et. al, ICRA 2015
Two-step Approach





Bai et. al, ICRA 2015
Solving POMDP using DESPOT

- STATE:
\((x_c,y_c,\theta_c,v_c, g_c)\)
corresponding to the 2D pose, speed and goal of the vehicle.
\((x_i,y_i,v_i, g_i)\)
corresponding to the \(i^{th}\) pedestrian's state
- ACTION:
$$\delta_s \in \{\textbf{Increase Speed, Decrease Speed,}$$ $$\textbf{Maintain Speed, Sudden Brake\}}$$
Effective
Roll-out Policy is important
Bai et. al, ICRA 2015
Two-step Approach
$$\delta_s \in \{\textbf{Increase Speed, Decrease Speed,}$$ $$\textbf{Maintain Speed, Sudden Brake\}}$$




Bai et. al, ICRA 2015
\(\textbf{1D-A}^*\) Approach
ISSUES?
- Decoupling of heading angle planning and speed planning often leads to unnecessary stalling of the vehicle!
- Hybrid A* path can't be found at at every time step!

Bai et. al, ICRA 2015
2D Approach

2D Approach

Solving POMDP using DESPOT
- STATE:
\((x_c,y_c,\theta_c,v_c, g_c)\)
corresponding to the 2D pose, speed and goal of the vehicle.
\((x_i,y_i,v_i, g_i)\)
corresponding to the \(i^{th}\) pedestrian's state
- ACTION:
$$\delta_s(t) \in \{\textbf{Increase Speed, Decrease Speed,}$$ $$\textbf{Maintain Speed, Sudden Brake\}}$$
Same as previous POMDP
- ACTION:
$$\mathcal{a = ( \delta_\theta , \delta_s )}$$
2D Approach
- Critical Challenge: Determining a good roll-out policy for the vastly increased set of states reachable in the tree search.



Effective roll-out policy
- Obtain a path using multi query motion planning technique
- Probabilistic RoadMap (PRM)
- Fast Marching Method (FMM)
- Roll-out policy: Execute a reactive controller over the obtained path

Probabilistic RoadMaps (PRM) for Multi-Query Path Planning






Simulation Environment
- Environment: \(100\)m x \(100\)m square field

-
Autonomous vehicle: A holonomic vehicle.
- Inspired by Kinova MOVO
- Max speed: \(2\) m/s

Experimental Scenarios



Scenario 1
(Open Field)
Scenario 2 (Cafeteria Setting)
Scenario 3
(L shaped lobby)
Planners
# possible actions in POMDP Planning: 4
# possible actions in POMDP Planning: 11


Experimental Details
- For each scenario, we ran sets of 100 different experiments with different pedestrian densities in the environment.



# humans = 100
# humans = 200
# humans = 300
# humans = 400
Scenario 1
Results
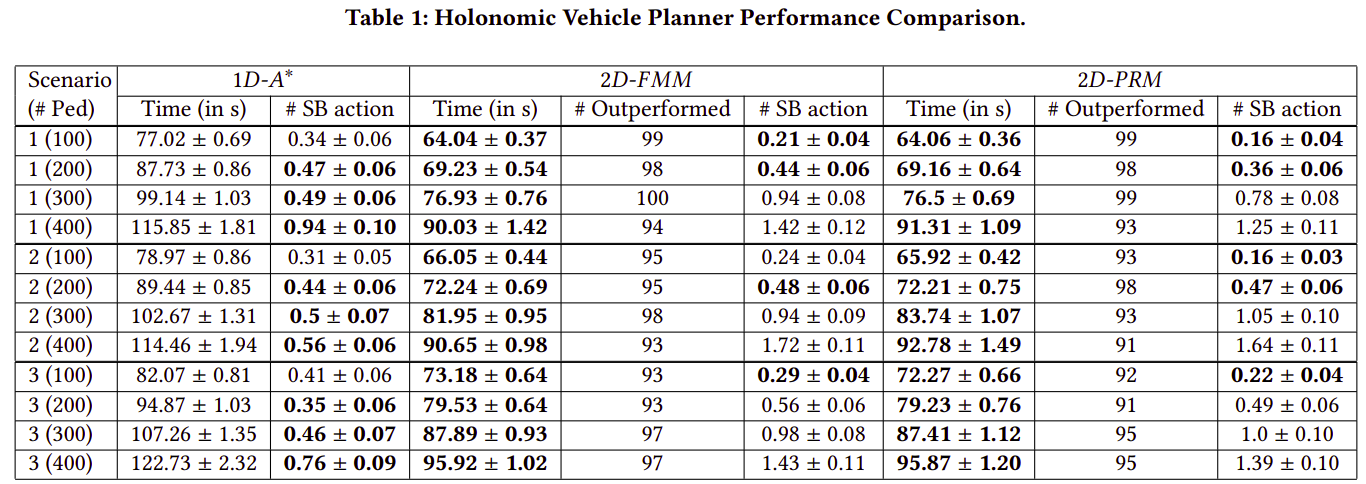
Evaluation Metric: Travel Time (in s)
Results

Evaluation Metric: #Outperformed
Scenario 2



\(1D-A^*\)
\(2D-FMM\)
\(2D-PRM\)
Results


Limited Space Planner
Extended Space Planner
Conclusion
Thank You!


Himanshu Gupta
himanshu.gupta@colroado.edu
Extended Space POMDP Planning
(AAMAS 2022)
https://github.com/himanshugupta1009/extended_space_navigation_pomdp


Summary
-
We proposed a new technique for navigation problems with arbitrary state uncertainty by incorporating multi-query path planning techniques for effective tree search using online solvers for a POMDP
- Probabilistic RoadMaps
-
Fast Marching Methods
- We demonstrated that our technique outperforms the current state-of-the-art method significantly in terms of travel time while being just as safe!
Experimental Details
- In simulations, the planning time for the vehicle at each step is 0.5 seconds


Experiments (NHV)
Limited Space
Planner
Extended Space
Planners
\(1D\)-\(A^*\)
\(2D\)-\(NHV\)


Results (NHV)

Evaluation Metric: Travel Time (in s)

Evaluation Metric: #Outperformed
Results (NHV)


\(1D-A^*\)
\(2D-NHV\)
Results (NHV)
AAMAS Conference Presentation
By Himanshu Gupta
AAMAS Conference Presentation
- 370



