
Algorithms for deception and counterdeception
Professor Zachary Sunberg
Autonomous Decision and Control Laboratory

-
Algorithmic Contributions
- Scalable algorithms for partially observable Markov decision processes (POMDPs)
- Motion planning with safety guarantees
- Game theoretic algorithms
-
Theoretical Contributions
- Particle POMDP approximation bounds
-
Applications
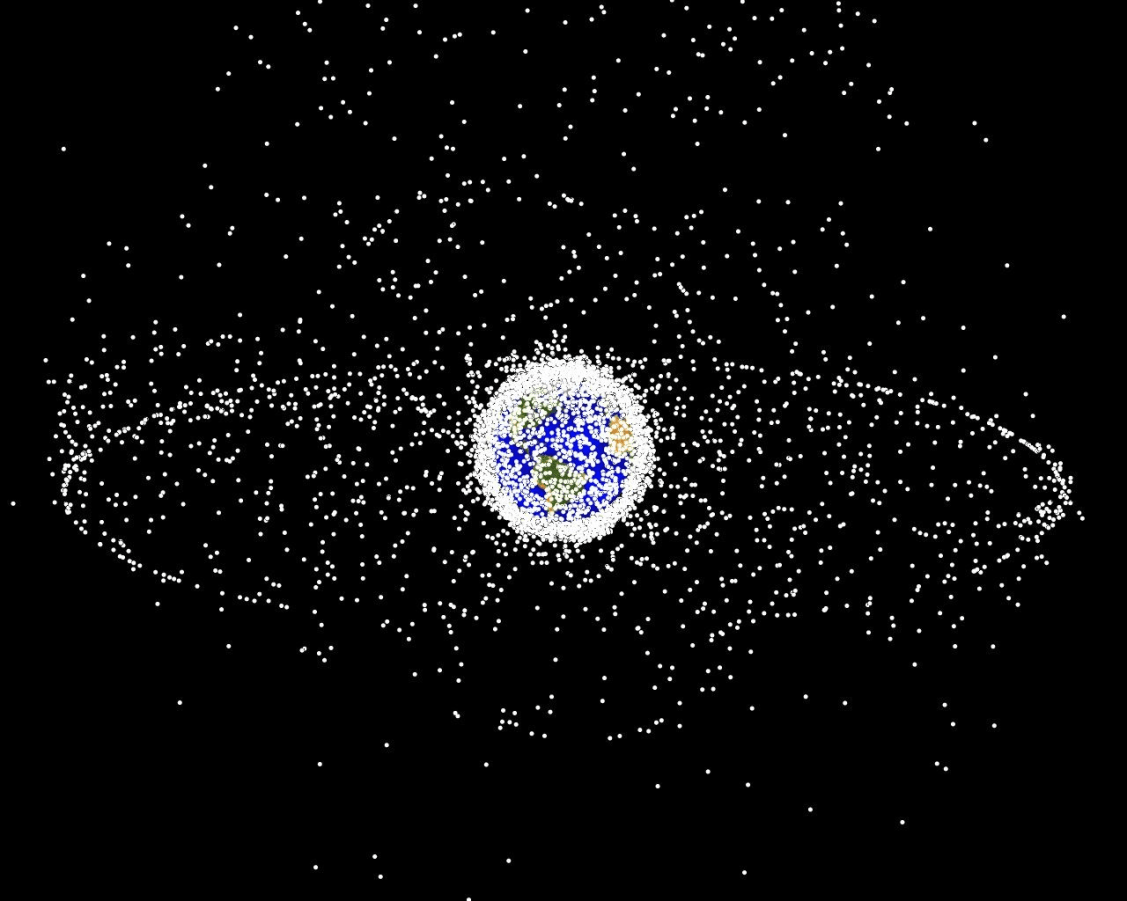
- Space Domain Awareness
- Autonomous Driving
- Autonomous Aerial Scientific Missions
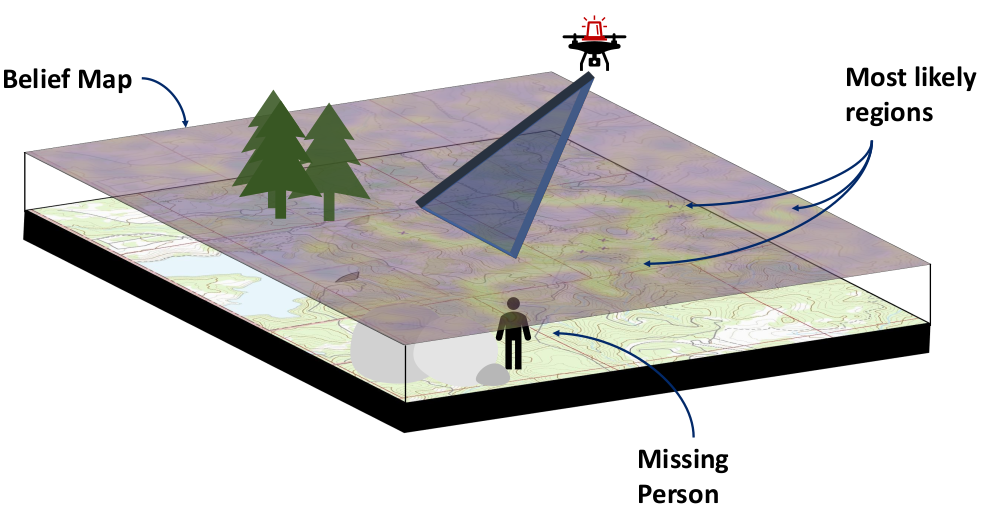
- Search and Rescue
- Space Exploration
- Ecology
-
Open Source Software
- POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students









Postdoc



BLUF
-
Game theory (GT) is a mathematical framework for reasoning about interactions.
- If there is partial observability, the best strategy may be stochastic (i.e. bluffing).
- Existing GT approaches have limitations for application in the physical world
- We can develop new mathematical tools and algorithms for deception and counterdeception
- Double Oracle with POMDPs
- Differential games (for D1)
- Tree search for (for D2)
- Scenario-based GT planning (for D2)
- Double Oracle with POMDPs
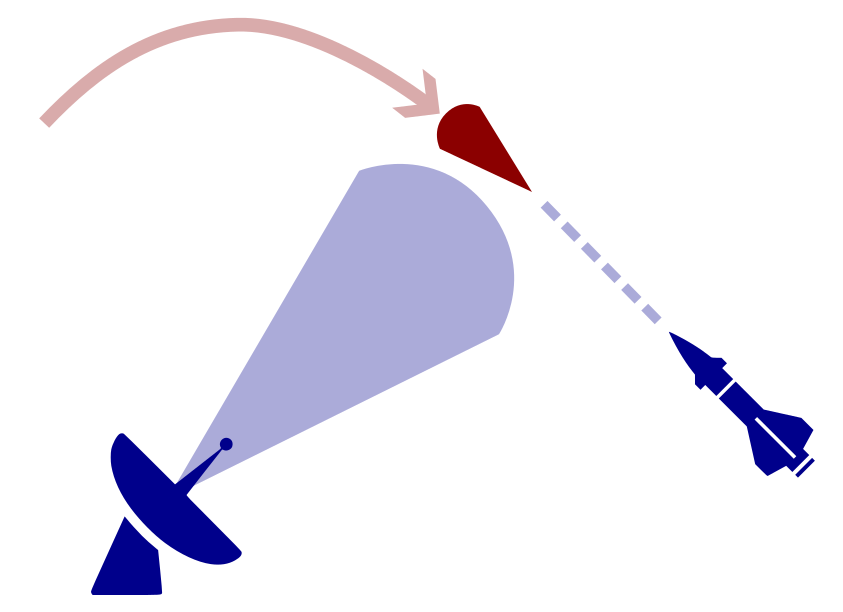
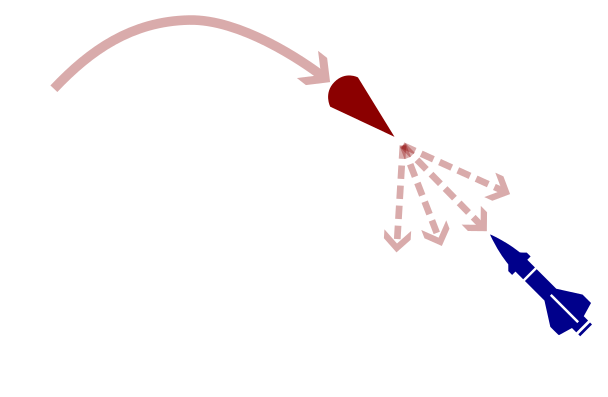
Defending against Maneuverable Hypersonic Weapons: the Challenge
Ballistic
Maneuverable Hypersonic
- Sense
- Estimate
- Intercept
Every maneuver involves tradeoffs
- Energy
- Targets
- Intentions
Game Theory
Nash Equilibrium: All players play a best response.
Optimization Problem
\(\text{subject to} \quad g(x) \geq 0\)
\(\text{maximize} \quad f(x)\)
Game
Player 1: \(U_1 (a_1, a_2)\)
Player 2: \(U_2 (a_1, a_2)\)
Collision
Example: Airborne Collision Avoidance
|
|
|
|
|
Player 1
Player 2
Up
Down
Up
Down
-6, -6
-1, 1
1, -1
-4, -4

Collision
Mixed Strategies
Nash Equilibrium \(\iff\) Zero Exploitability
\[\sum_i \max_{\pi_i'} U_i(\pi_i', \pi_{-i})\]
No Pure Nash Equilibrium!
Instead, there is a Mixed Nash where each player plays up or down with 50% probability.
If either player plays up or down more than 50% of the time, their strategy can be exploited.
Exploitability (zero sum):
Hypersonic Missile Defense (simplified)
|
|
|
|
|
Attacker
Defender
Up
Down
Up
Down
-1, 1
1, -1
1, -1
-1, 1
Collision
Collision
Strategy (\(\pi_i\)): probability distribution over actions
Three Domains for GT in Hypersonic Defense
Domain 1: Onboard Vehicle Control
Domain 2: Battlespace Management

Domain 3: Arsenal Design


Existing Tools
Differential Games

- High precision control
- Assumes full observability
Deep Reinforcement Learning
Image: DeepMind
- Superhuman Performance
- Solves Biggest Problems
- Slow Offline Training
Incomplete Information Game Theory
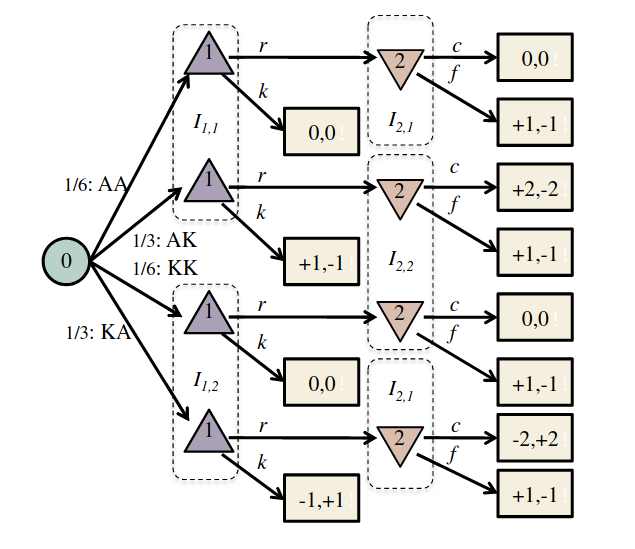

- Mixed Strategies/Bluffing
- Discrete Board-game-like Problems
- Computational Load
*Partially observable Markov decision process
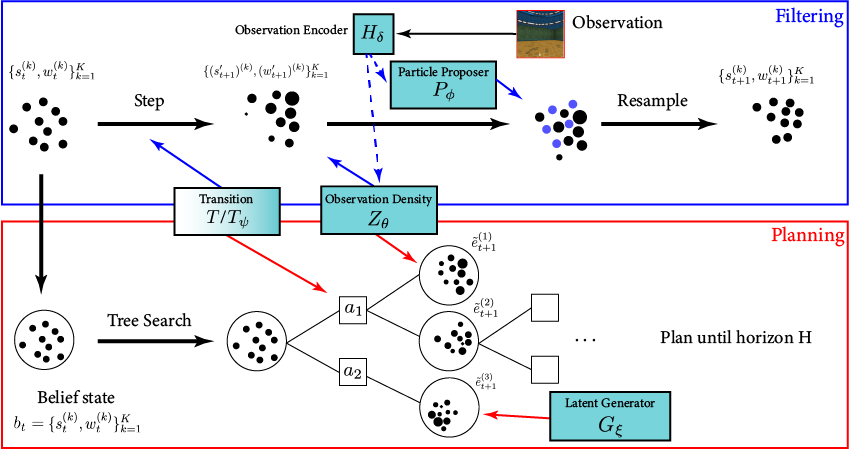
POMDP* Planning


- Partial Observability
- Single Player (just an optimization problem)
Our Innovation: \(\mathcal{S}\)- and \(\mathcal{O}\)-independent algorithms for POMGs

Incomplete Information Extensive form Game
Our new algorithm for POMGs
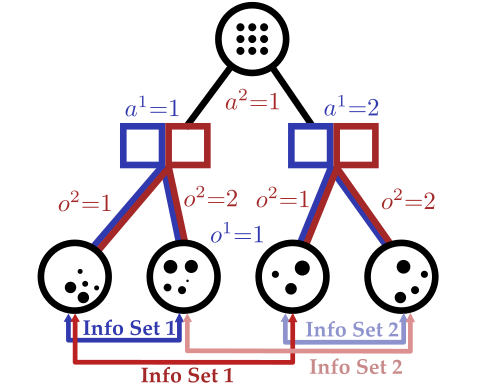
Innovation 1: Double Oracle (DO) with POMDPs

|
|
||
|
|
||
|
|






Default Strategy Profile
Mix Pure Strategies
Add Best Response to Pure Strategy Set
Compute Best Response
(Solve POMDP)
\[\hat{x}', \Sigma' = \text{Filter}(\hat{x}, \Sigma, y, \pi_1)\]
\[u = \tilde{u} -K(\hat{x} - \tilde{x})\]

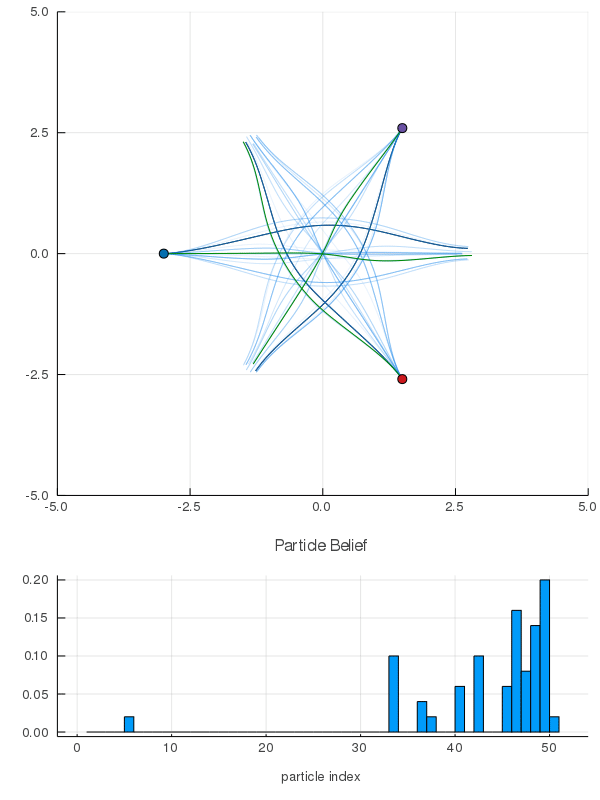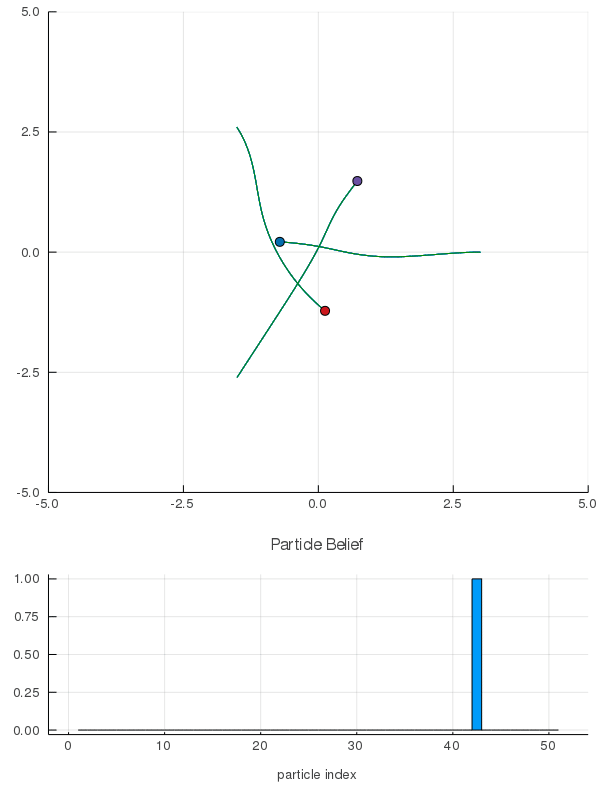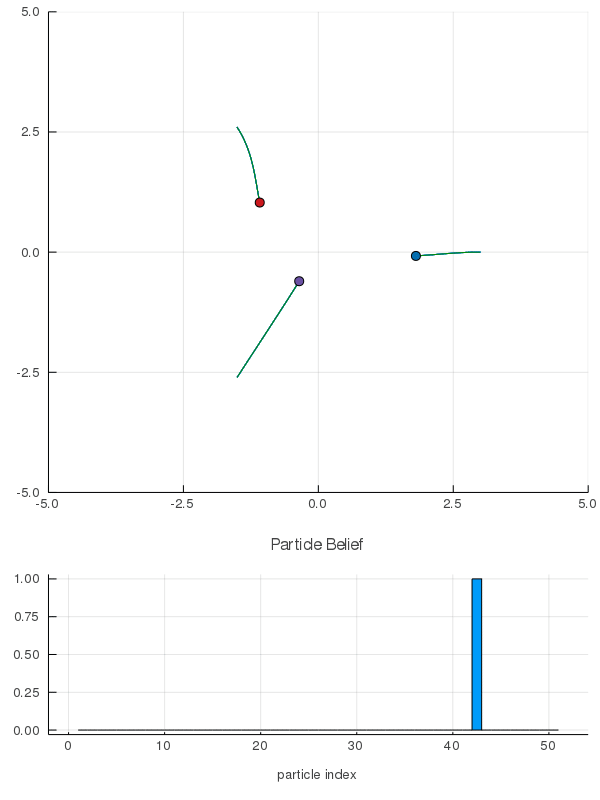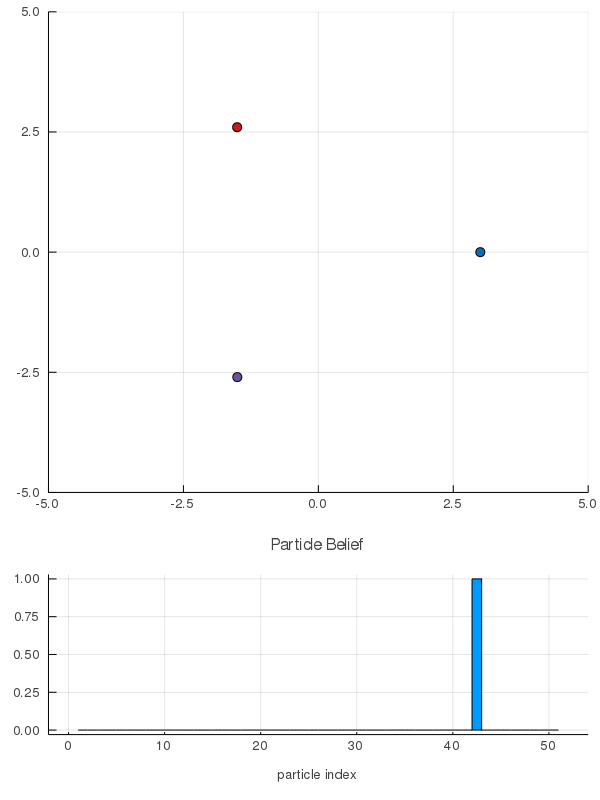
DO Applied to Domain 1: Online Differential Games
[Peters, Sunberg, et al. 2020]

2 ms solve time with warm starting
DO Applied to Domain 1: Online Differential Games



< 3 min offline training, 2 ms online computation

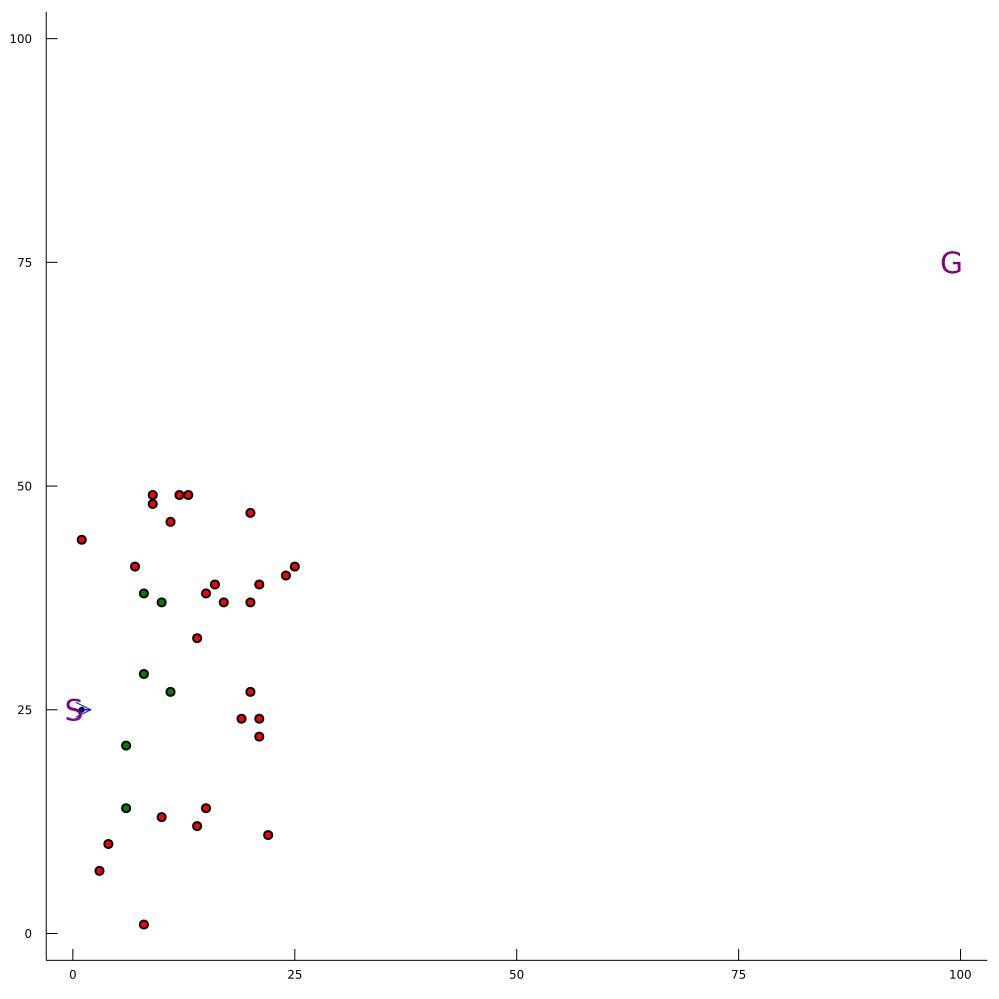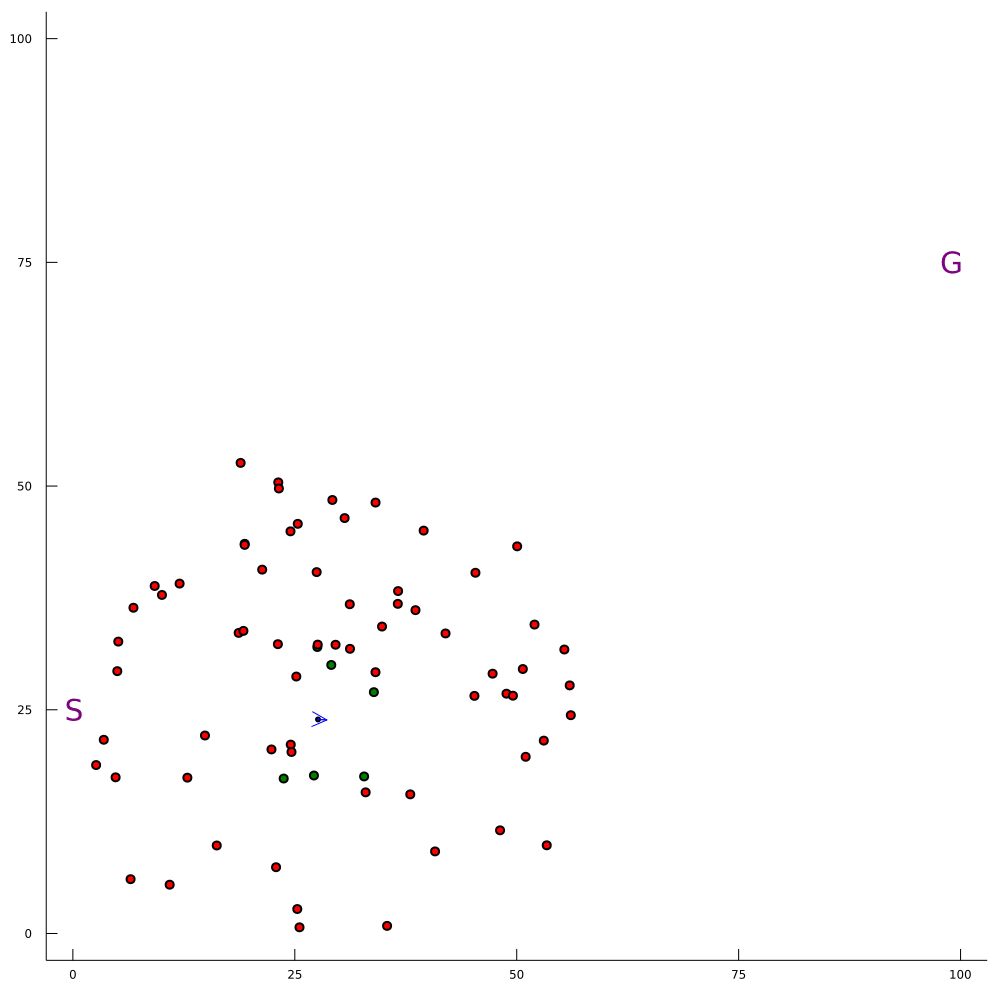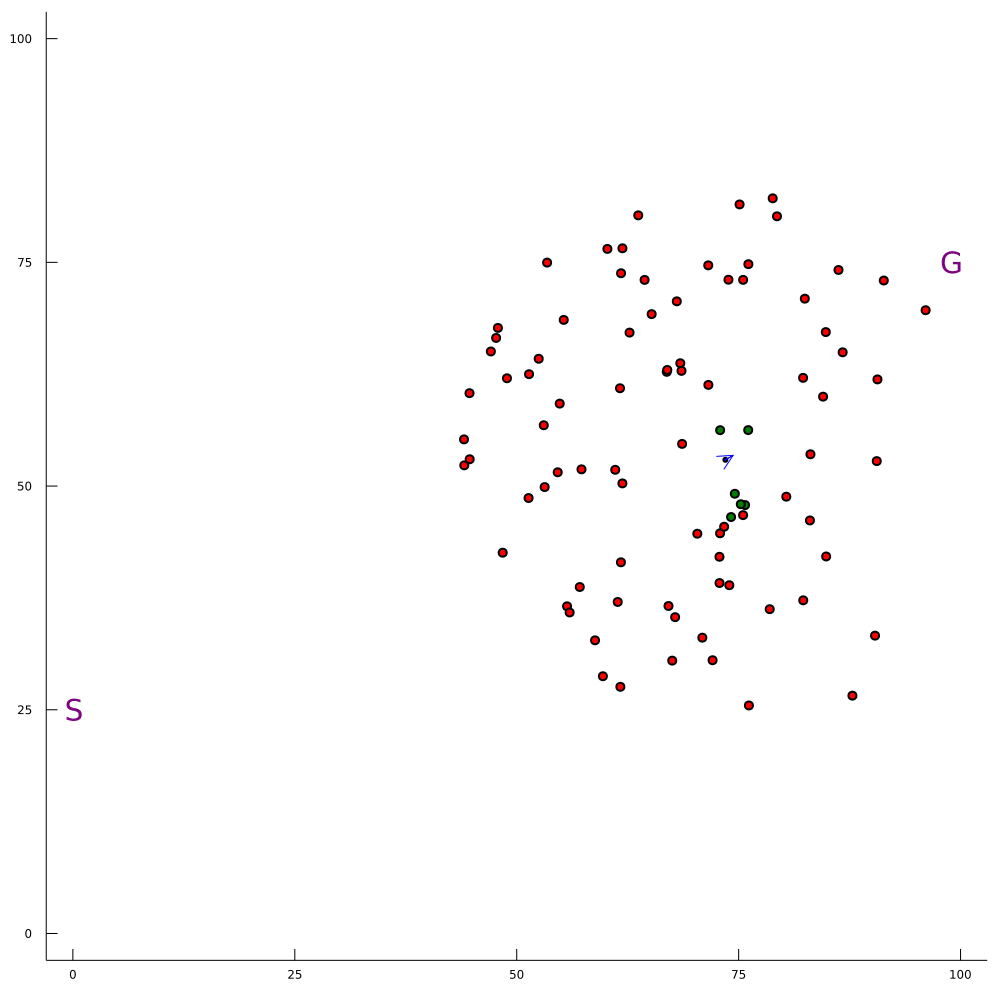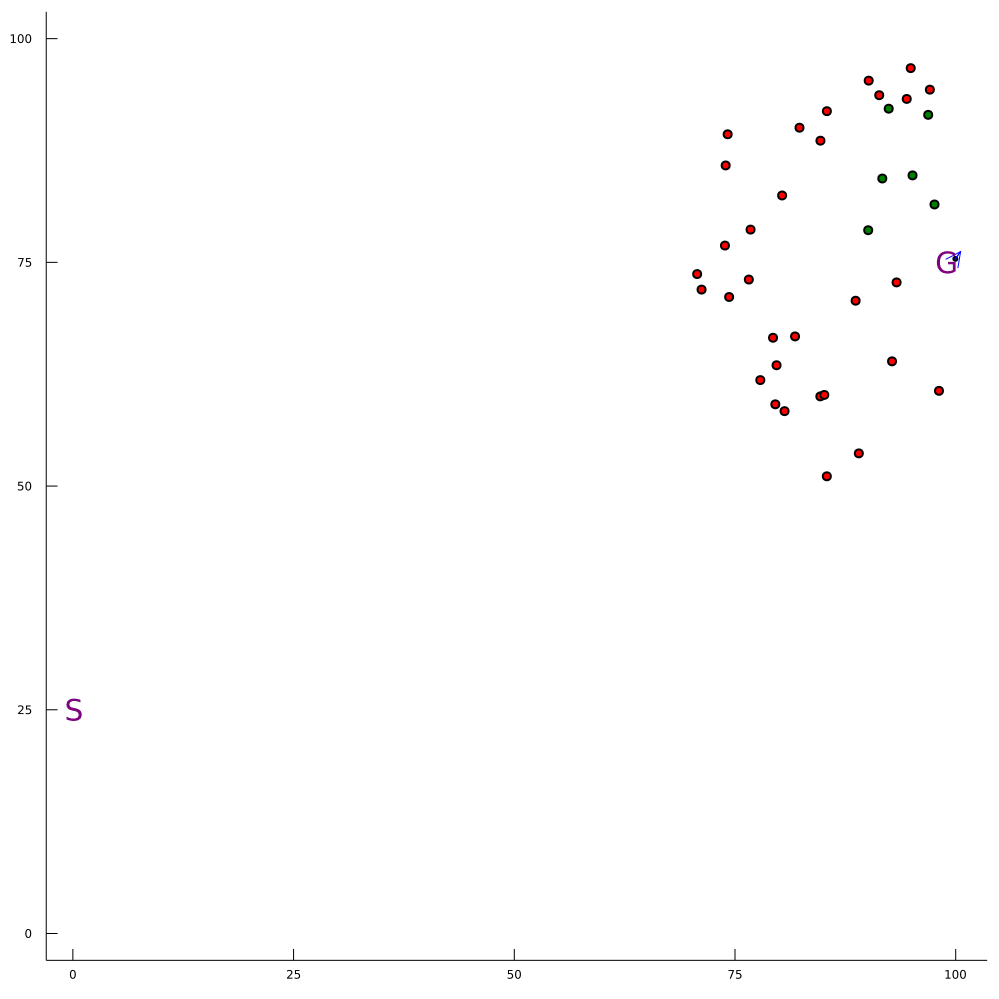
Our Expertise: Solving POMDPs Online
100-1000 ms online planning
[Sunberg and Kochenderfer, 2018]
[Sunberg and Kochenderfer, 2022]
[Gupta, Hayes, and Sunberg, 2022]
[Lim, Sunberg, et al. (in prep)]

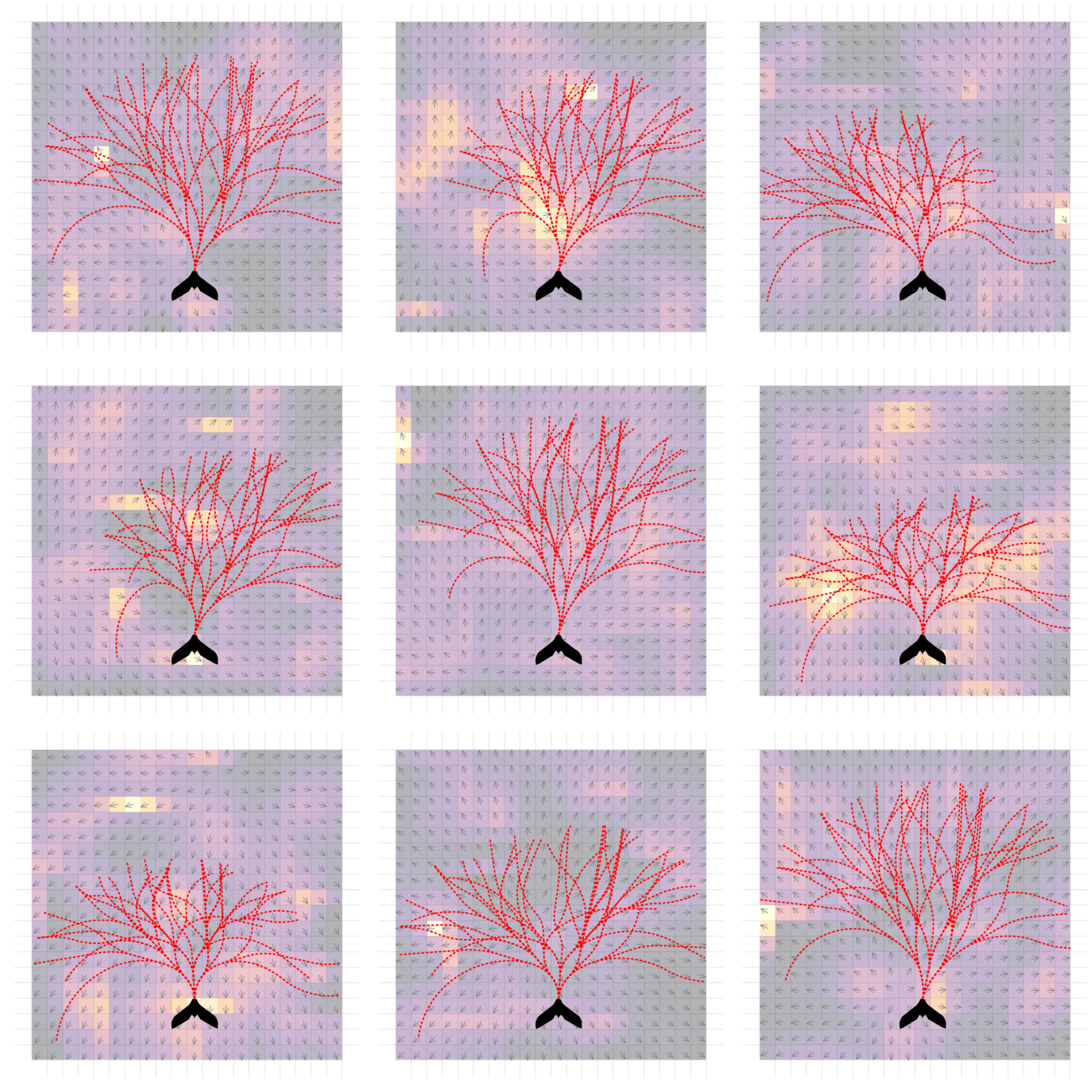
Breaking the Curse of Dimensionality in POMDPs
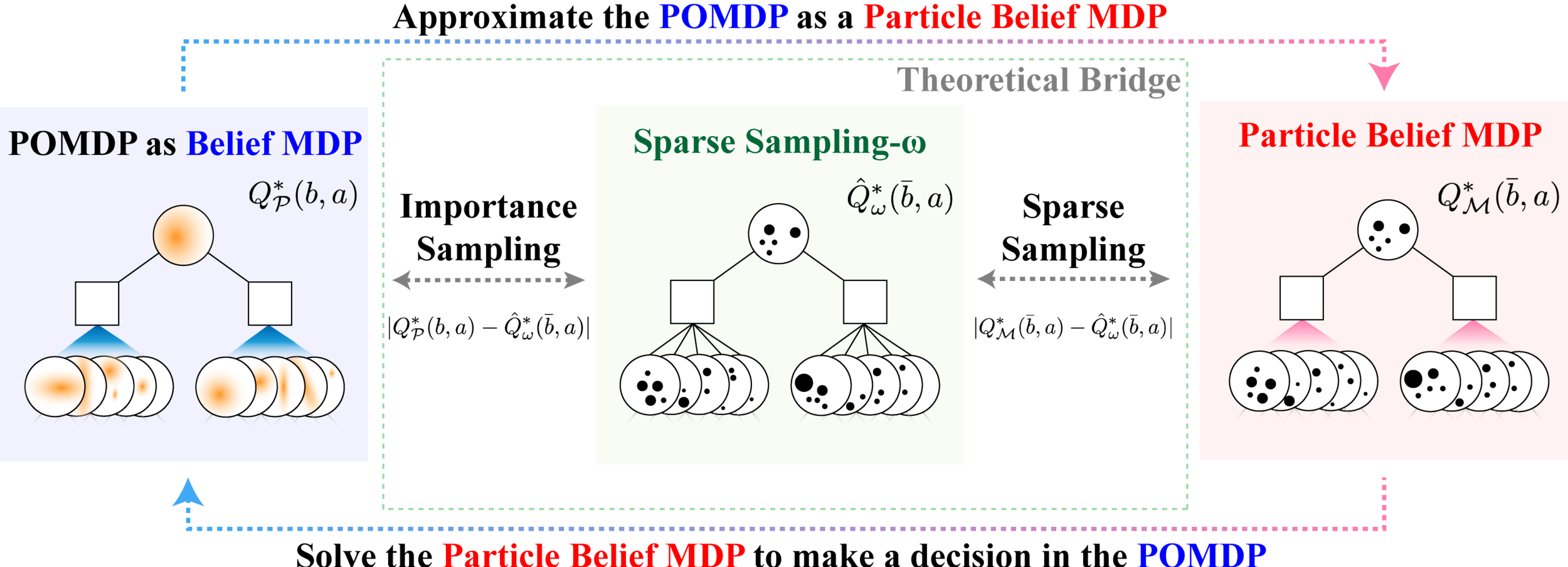
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]
For any \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,
[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]
No dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!
Storm Science
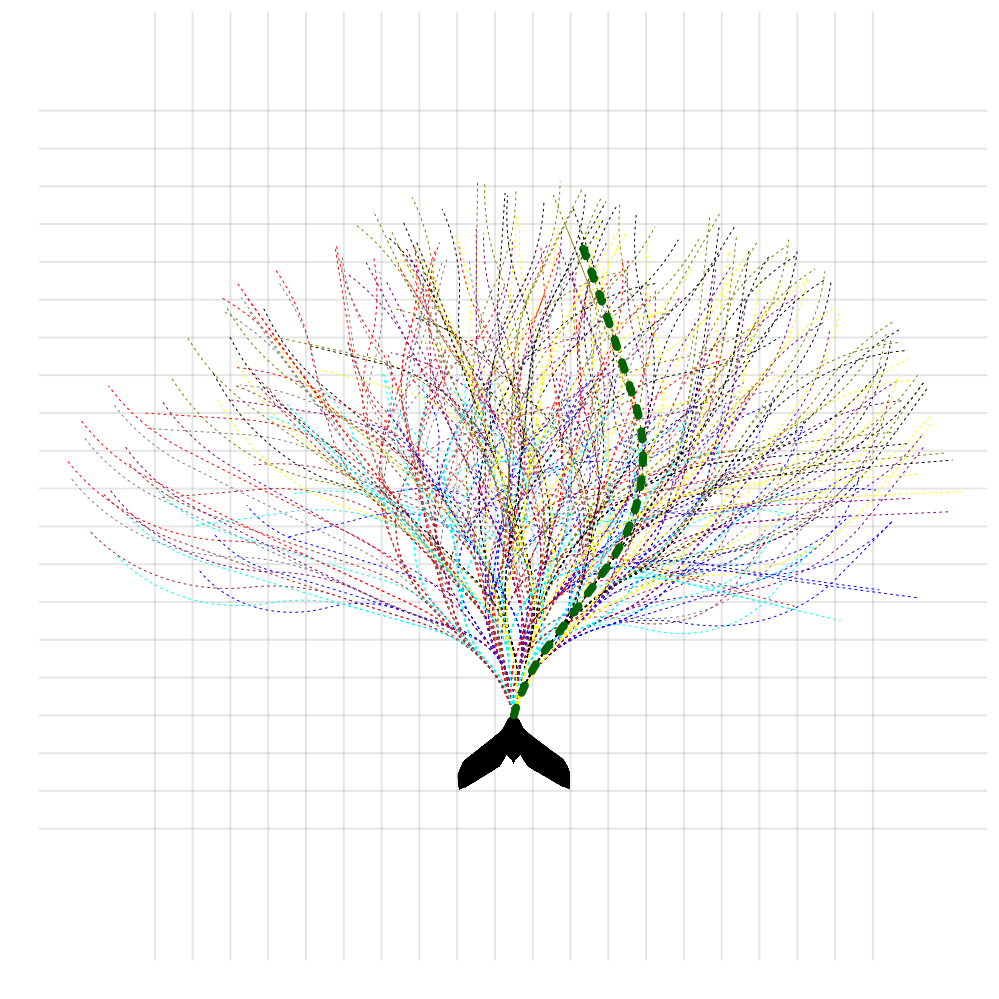


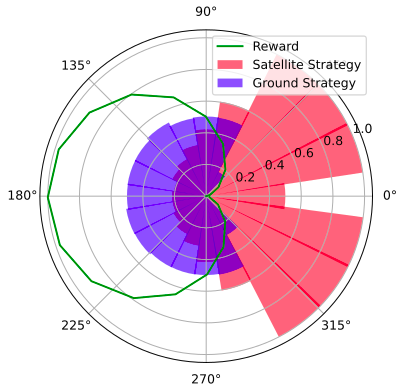
Simplified Space Domain Awareness Game

1
2
...
...
...
...
...
...
...
\(N\)
[Becker & Sunberg AMOS 2021]
Counterfactual Regret Minimization Training
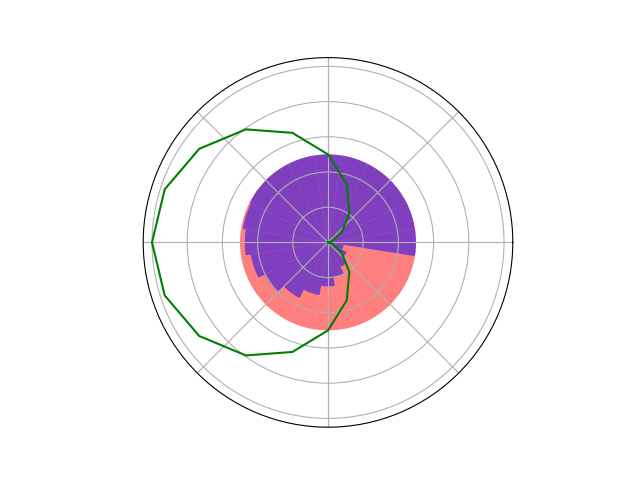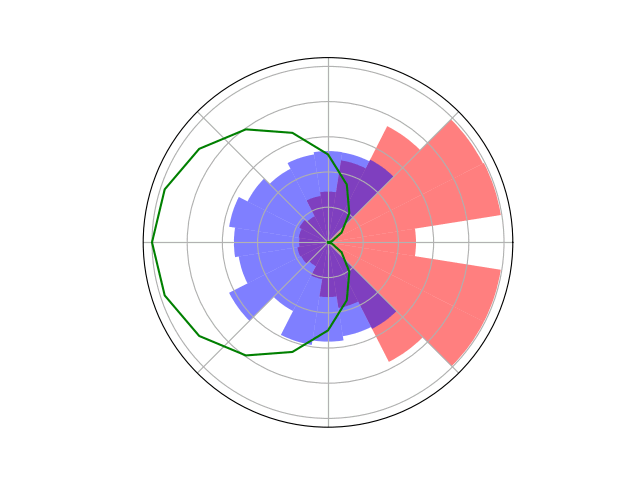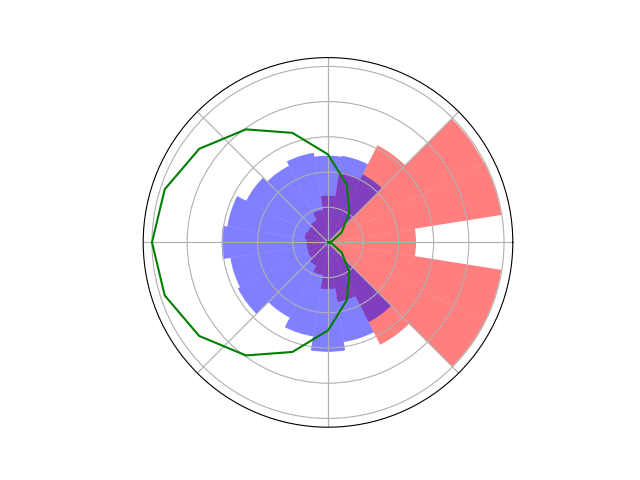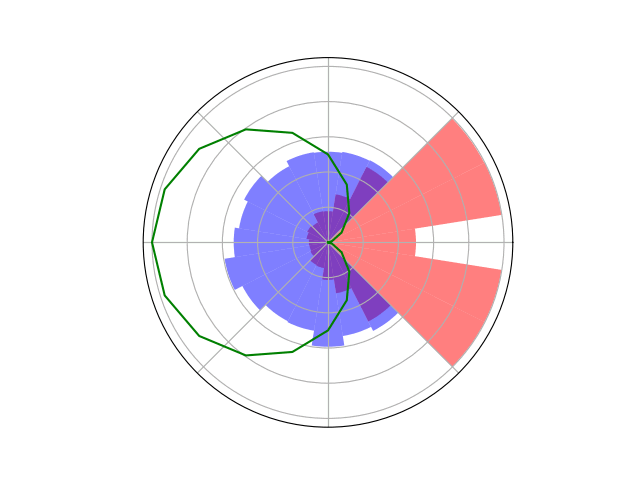
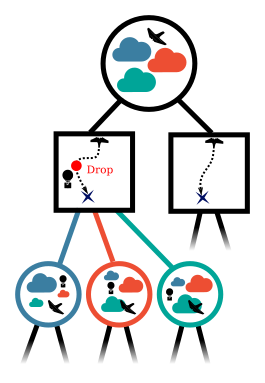
Innovation 2: Scenario-Based GT Planning

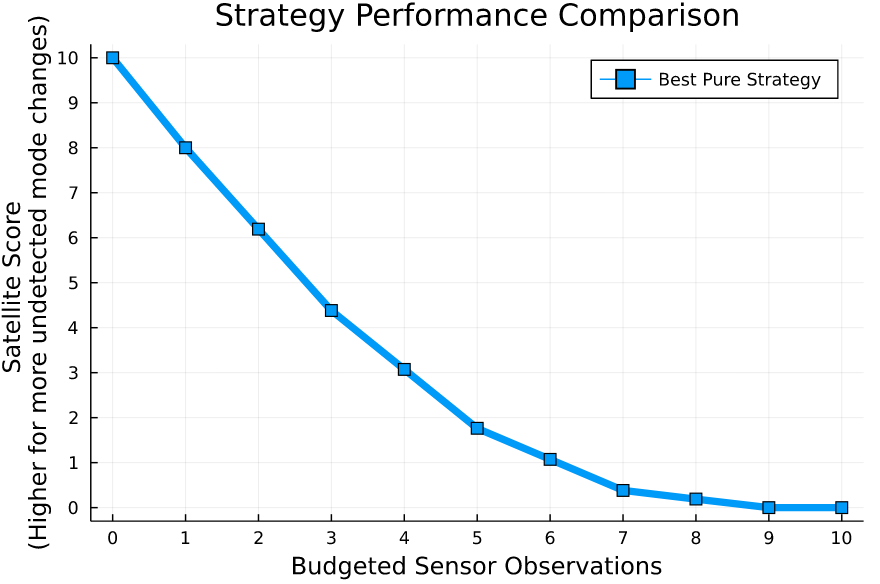
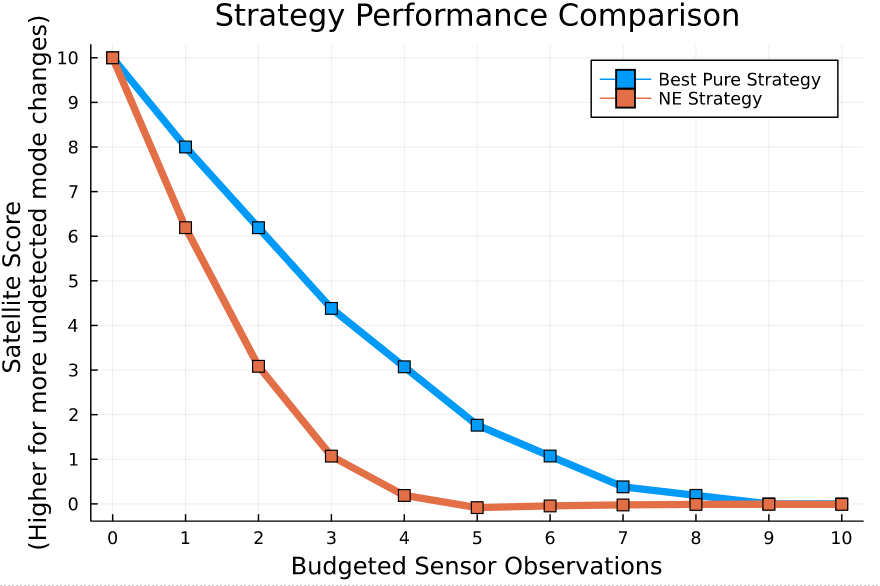
Issue: Current counterfactual regret (CFR) techniques have large computation requirements because of high variance due to random sampling
Solution: Scenario-based GT planning (idea borrowed from POMDP research)


[Somani et al. 2017]
[Garg et al. 2019]
What We Need
-
Funding
- Students
(~$100k per year incl. overhead) - Faculty and Staff
- Computing Resources
- Students
-
Guidance/representative models
- Unclassified for most work
- Pipeline to high-fidelity simulation
Notional timeline (2 Faculty, 3 Students):
Apply existing diff. game approaches
Develop and implement feedback diff. game algorithms
Teach advanced dynamic GT class
Months:
Test in high fidelity simulation
Diff. games for onboard control
POMDP DO for battlespace mgmt
Scenario-based GT Planning
6
12
18
24
32
36
implement on representative PO Markov game
Develop decentralized composable algorithm
Other
Organize workshop at conference
Develop and imlement basic algorithm
Test in realistic simulation
Develop Mathematical Theory
Test in realistic simulation
Deliverables: Reference implementations
Hybrid Games
Student Internship at contractor
Additional Material



Our Expertise
Game Theory for Space Domain Awareness
Our Expertise
Open Source Julia Software

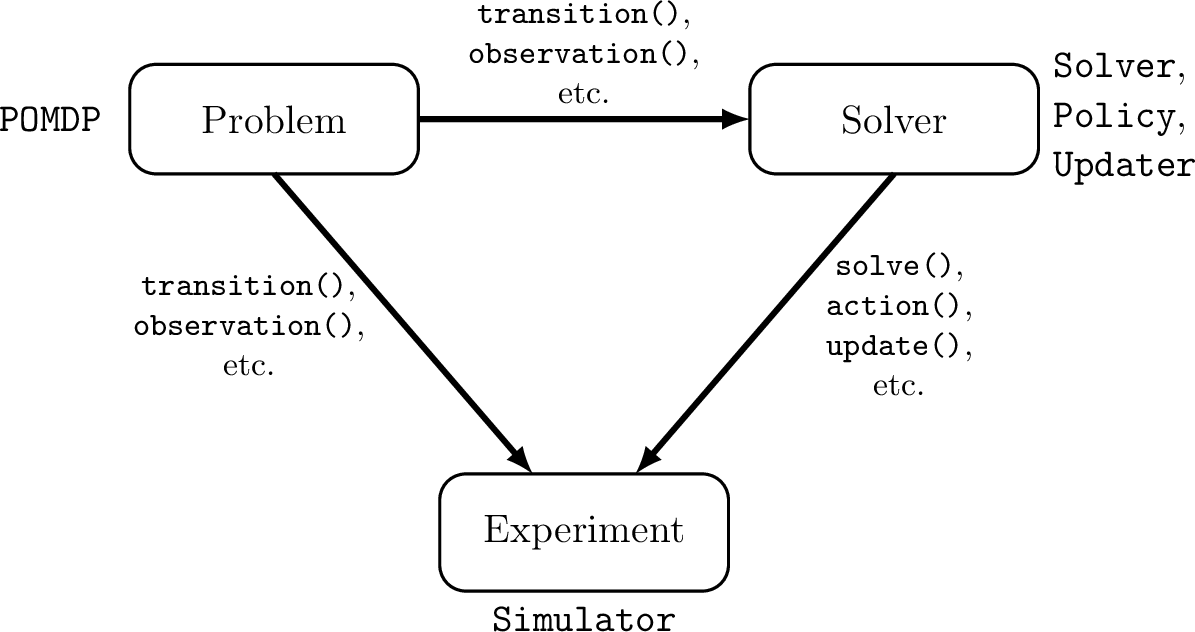

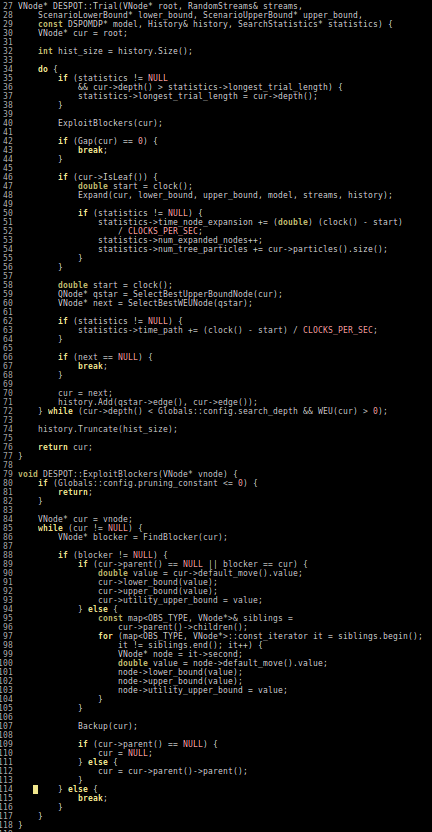
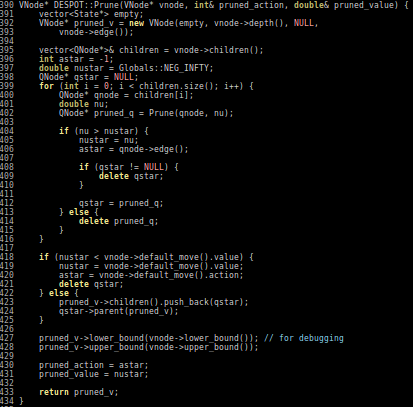
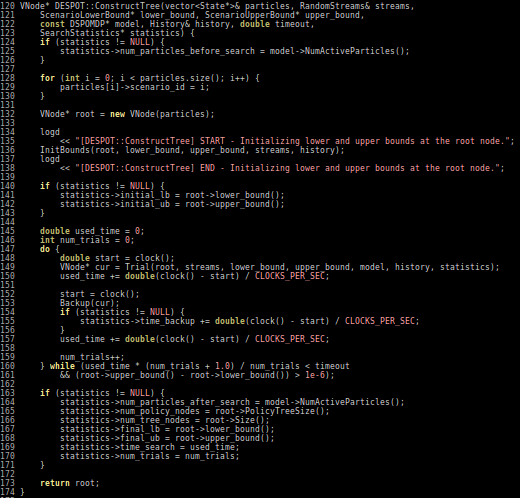
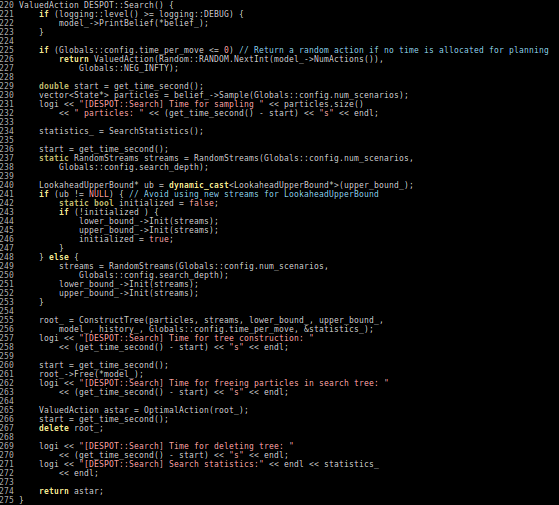
POMDPs.jl - An interface for defining and solving MDPs and POMDPs
- Executes fast as C
- As easy to write and read as Python/MATLAB


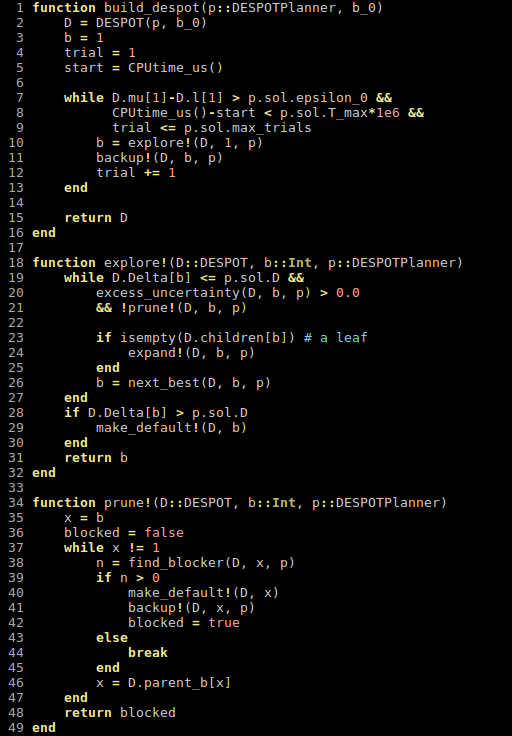


Our Technical Approach

- Partially Observable Markov Games
- Principled Tractable Approximations
- Online Solutions First
- Focus on Composability
- Fast Prototyping in Julia
Research Model
Mathematical Frameworks
Algorithm Development
Realistic Simulation
Physical Tests
Proposed Research

Develop
- Mathematical Frameworks
- Algorithms
to compute unexploitable strategies for hypersonic weapon defense systems
Probability distributions describing what all players should do
Game Theory
Nash Equilibrium: All players play a best response.
Example: Stag Hunt
Optimization Problem
\(\text{subject to} \quad g(x) \geq 0\)
\(\text{maximize} \quad f(x)\)
Game
Player 1: \(U_1 (a_1, a_2)\)
Player 2: \(U_2 (a_1, a_2)\)
Strategy (\(\pi_i\)): probability distribution over actions
|
|
|
|
|
Player 1
Player 2
Stag
Hare
Stag
Hare
10, 10
1, 8
5, 5
8, 1
