Towards Tree Search in Partially Observable Stochastic Games

 

Assistant Professor Zachary Sunberg

University of Colorado Boulder

October 8th, 2025

Autonomous Decision and Control Laboratory

cu-adcl.org

  • Algorithmic Contributions
    • Scalable algorithms for partially observable Markov decision processes (POMDPs)
    • Motion planning with safety guarantees
    • Game theoretic algorithms
  • Theoretical Contributions
    • Particle POMDP approximation bounds
  • Applications
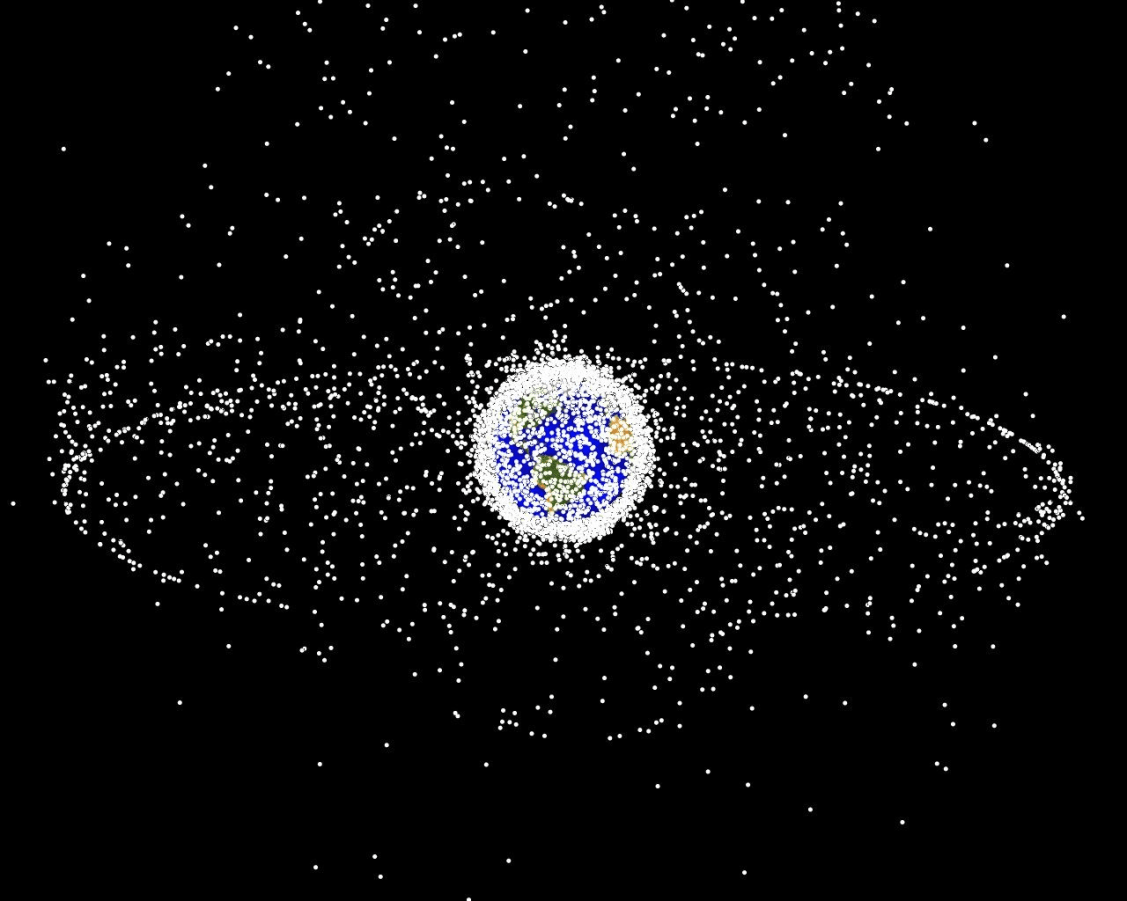
    • Space Domain Awareness
    • Autonomous Driving
    • Autonomous Aerial Scientific Missions
    • Search and Rescue
    • Space Exploration
    • Ecology
  • Open Source Software
    • POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students

Postdoc

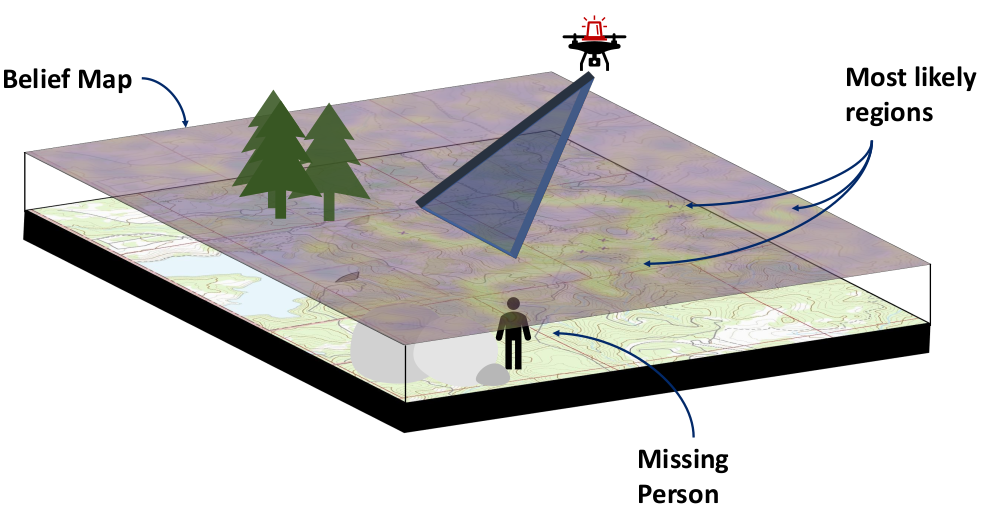
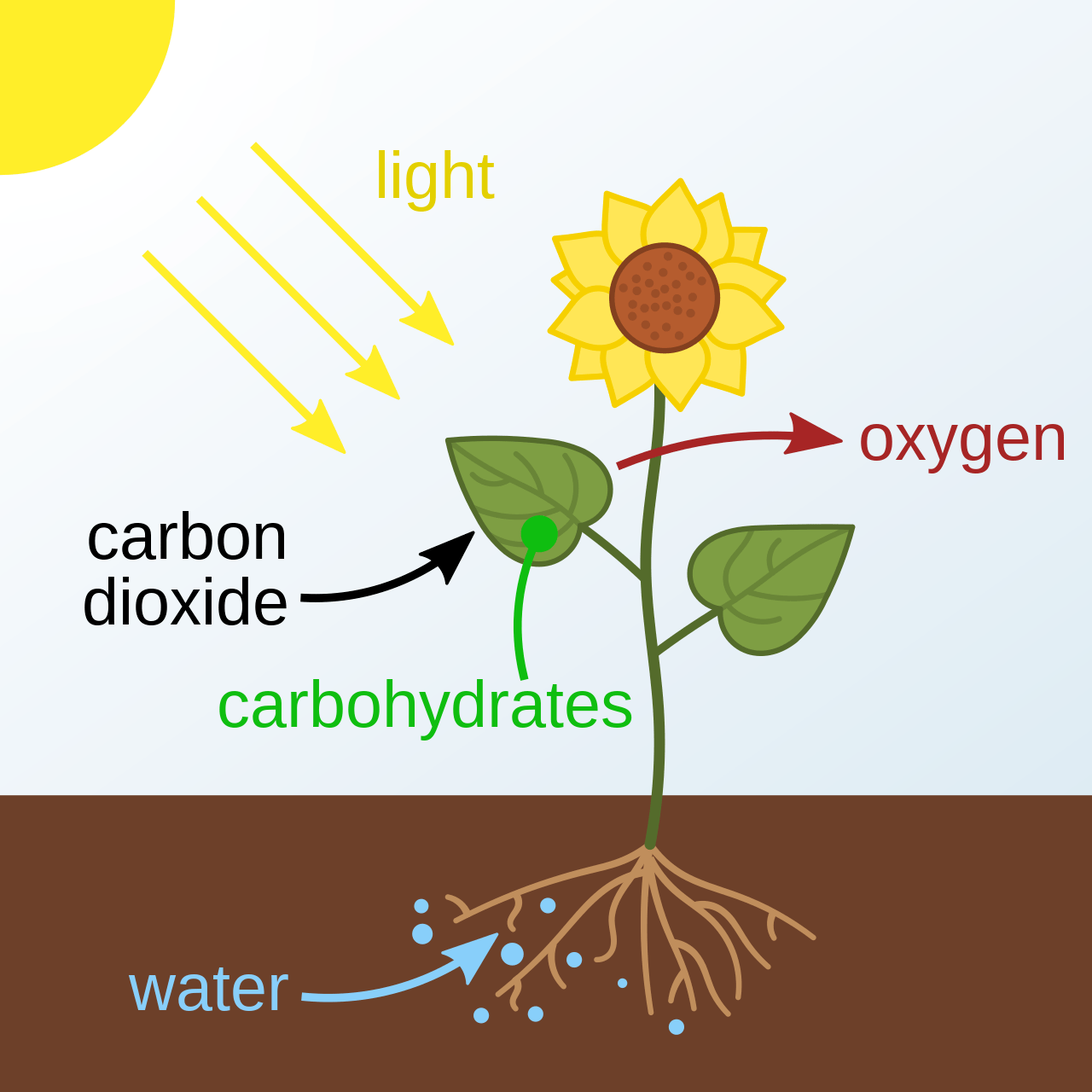
Towards Efficient Tree Search in POSGs

  1. Taxonomy for Decision Making under Uncertainty
  2. Breaking the curse of dimensionality in POMDPs
  3. Steps toward tree search in POSGs
    1. Simultaneous Moves
    2. State Uncertainty: CDITs
    3. Online Planning

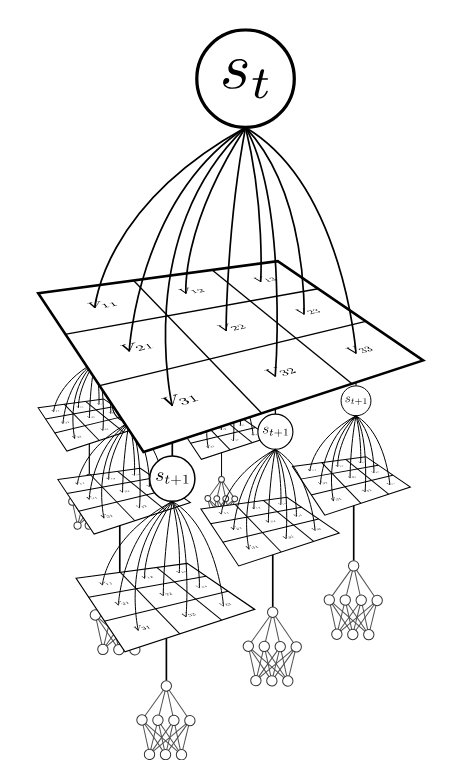
Part I: Types of Uncertainty

Types of Uncertainty

Aleatory

Epistemic (Static)

Epistemic (Dynamic)

Interaction

MDP

RL

POMDP

Game

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Aleatory

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)

\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)

\[\underset{\pi:\, \mathcal{S} \to \mathcal{A}}{\text{maximize}} \quad \text{E}\left[ \sum_{t=0}^\infty R(s_t, a_t) \right]\]

Reinforcement Learning

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Aleatory

Epistemic (Static)

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)

\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)

Partially Observable Markov Decision Process (POMDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
  • \(\mathcal{O}\) - Observation space
  • \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution

Aleatory

Epistemic (Static)

Epistemic (Dynamic)

\([x, y, z,\;\; \phi, \theta, \psi,\;\; u, v, w,\;\; p,q,r]\)

\(\mathcal{S} = \mathbb{R}^{12}\)

\(\mathcal{S} = \mathbb{R}^{12} \times \mathbb{R}^\infty\)

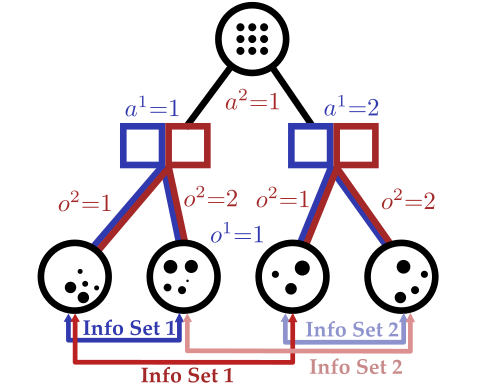
Partially Observable Stochastic Game (POSG)

Aleatory

Epistemic (Static)

Epistemic (Dynamic)

Interaction

  • \(\mathcal{S}\) - State space
  • \(T(s' \mid s, \bm{a})\) - Transition probability distribution
  • \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
  • \(R^i(s, \bm{a})\) - Reward function (cooperative, opposing, or somewhere in between)
  • \(\mathcal{O}^i, \, i \in 1..k\) - Observation spaces
  • \(Z(o^i \mid \bm{a}, s')\) - Observation probability distributions

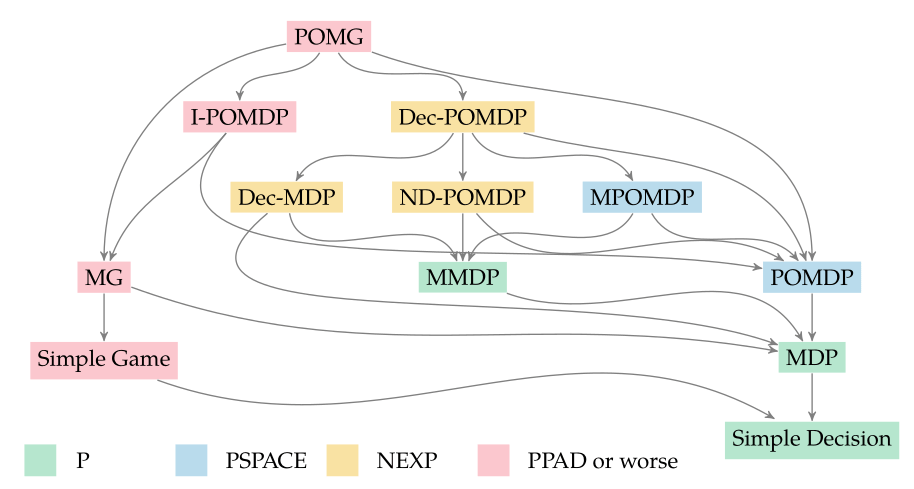
Hierarchy of Problems

Part II: Breaking the Curse of Dimensionality in POMDPs

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, |s-10|) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

Goal: \(a=0\) at \(s=0\)

Optimal Policy

Localize

\(a=0\)

POMDP Example: Light-Dark

Solving a POMDP

Environment

Belief Updater

Planner

\(a = +10\)

True State

\(s = 7\)

Observation \(o = -0.21\)

\(b\)

\[b_t(s) = P\left(s_t = s \mid b_0, a_0, o_1 \ldots a_{t-1}, o_{t}\right)\]

\[ = P\left(s_t = s \mid b_{t-1}, a_{t-1}, o_{t}\right)\]

\(Q(b, a)\)

\(O(|\mathcal{S}|^2)\)

Why are POMDPs difficult?

  1. Curse of History
  2. Curse of dimensionality
    1. State space
    2. Observation space
    3. Action space

Tree size: \(O\left(\left(|A||O|\right)^D\right)\)

Curse of Dimensionality

\(d\) dimensions, \(k\) segments \(\,\rightarrow \, |S| = k^d\)

1 dimension

e.g. \(s = x \in S = \{1,2,3,4,5\}\)

\(|S| = 5\)

2 dimensions

e.g. \(s = (x,y) \in S = \{1,2,3,4,5\}^2\)

\(|S| = 25\)

3 dimensions

e.g. \(s = (x,y,x_h) \in S = \{1,2,3,4,5\}^3\)

\(|S| = 125\)

(Discretize each dimension into 5 segments)

\(x\)

\(y\)

\(x_h\)

Integration

Find \(\underset{s\sim b}{E}[f(s)]\)

\[=\sum_{s \in S} f(s) b(s)\]

Monte Carlo Integration

\(Q_N \equiv \frac{1}{N} \sum_{i=1}^N f(s_i)\)

\(s_i \sim b\)     i.i.d.

\(\text{Var}(Q_N) = \text{Var}\left(\frac{1}{N} \sum_{i=1}^N f(s_i)\right)\)

\(= \frac{1}{N^2} \sum_{i=1}^N\text{Var}\left(f(s_i)\right)\)

\(= \frac{1}{N} \text{Var}\left(f(s_i)\right)\)

\[P(|Q_N - E[f(s_i)]| \geq \epsilon) \leq \frac{\text{Var}(f(s_i))}{N \epsilon^2}\]

(Bienayme)

(Chebyshev)

Curse of dimensionality!

Sparse Sampling for MDPs

Expand for all actions (\(\left|\mathcal{A}\right| = 2\) in this case)

...

Expand for all \(\left|\mathcal{S}\right|\) states

\(C=3\) states

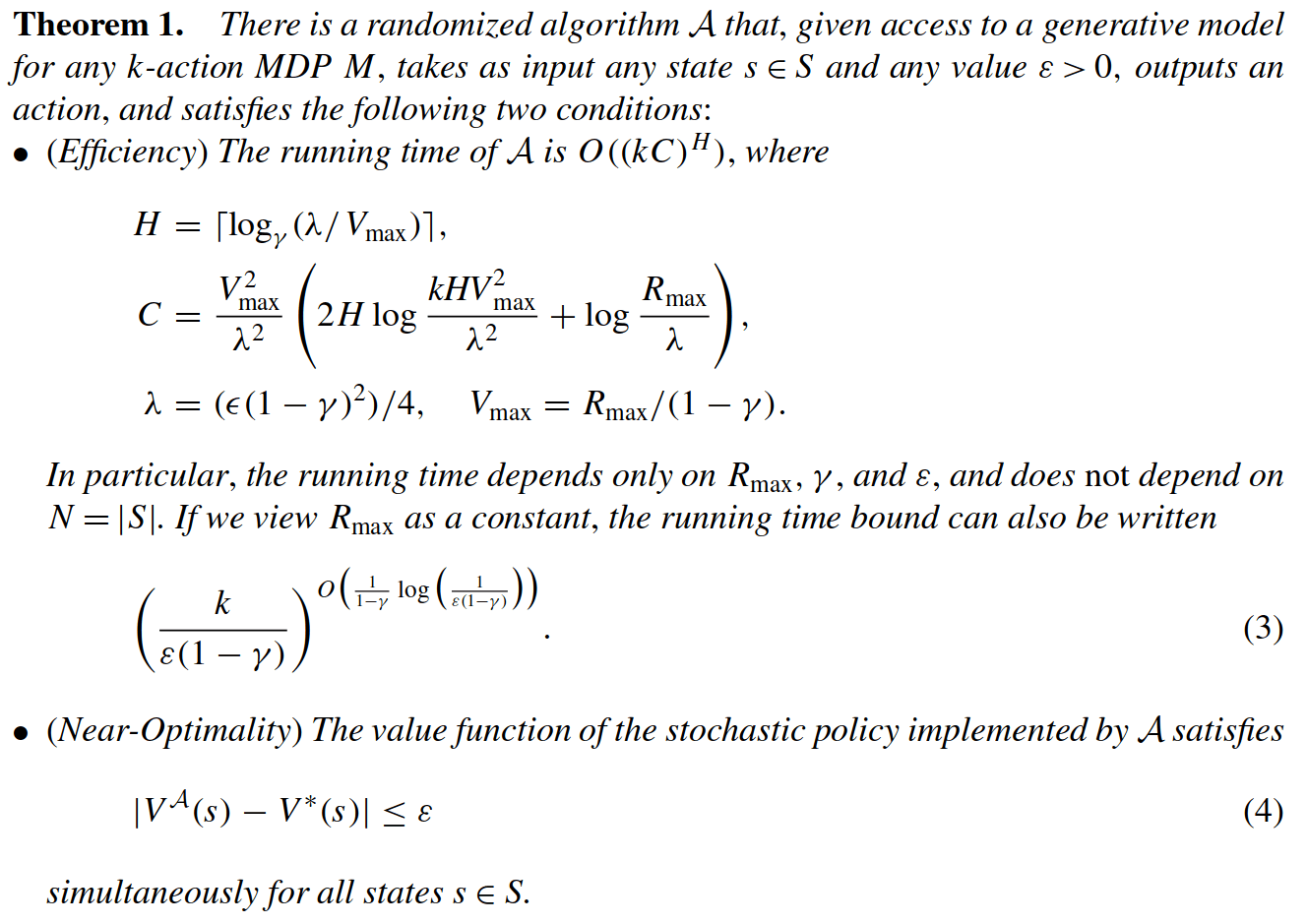
Particle Filter POMDP Approximation

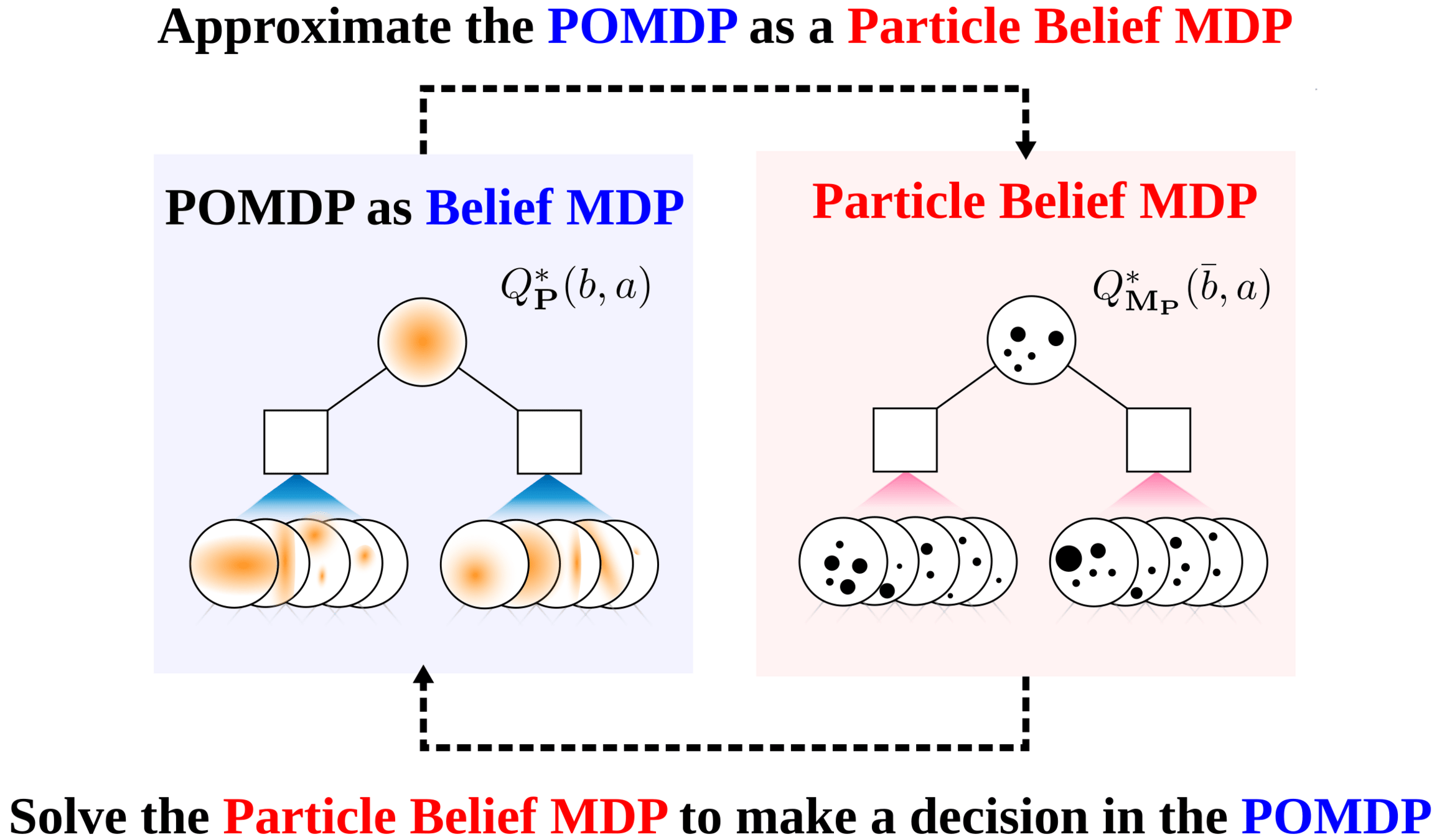
\[b(s) \approx \sum_{i=1}^N \delta_{s}(s_i)\; w_i\]

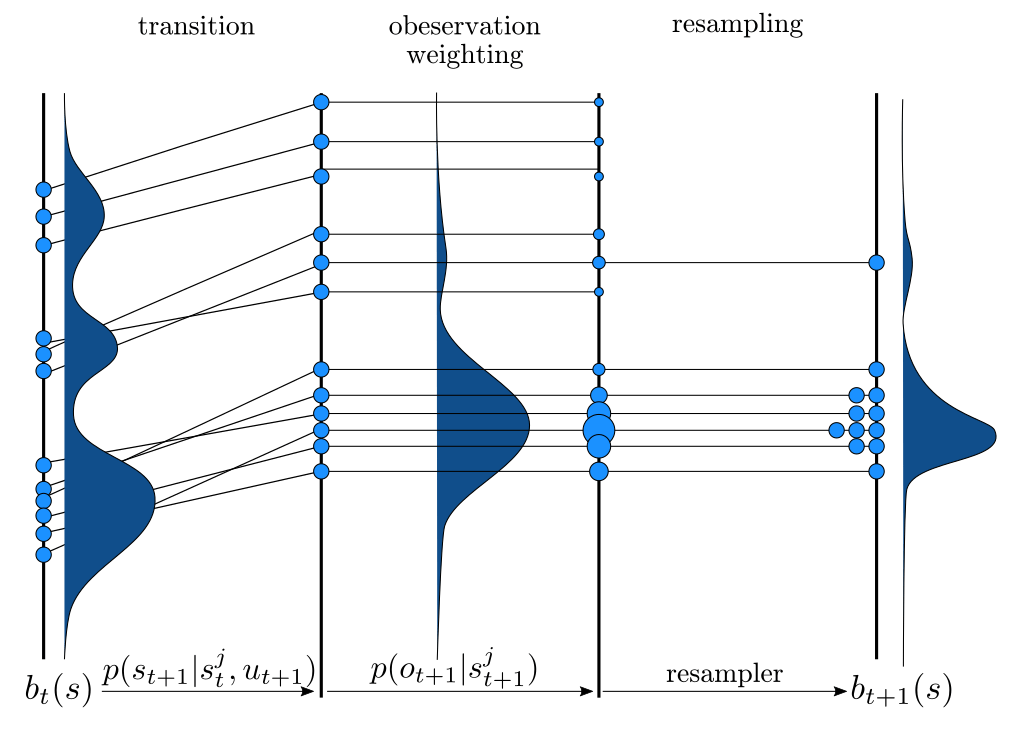
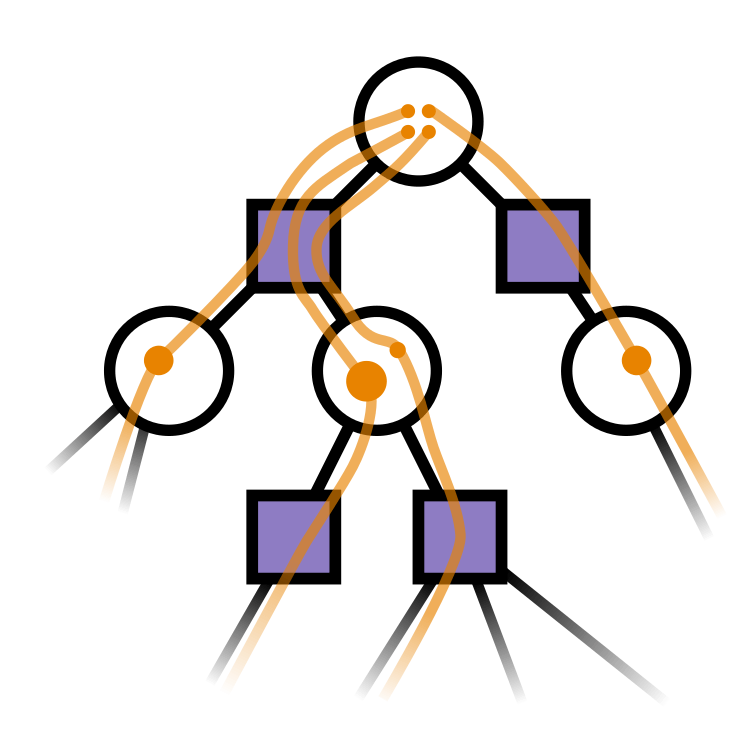
[Sunberg and Kochenderfer, ICAPS 2018, T-ITS 2022]

How do we prove convergence?

PF Approximation Accuracy

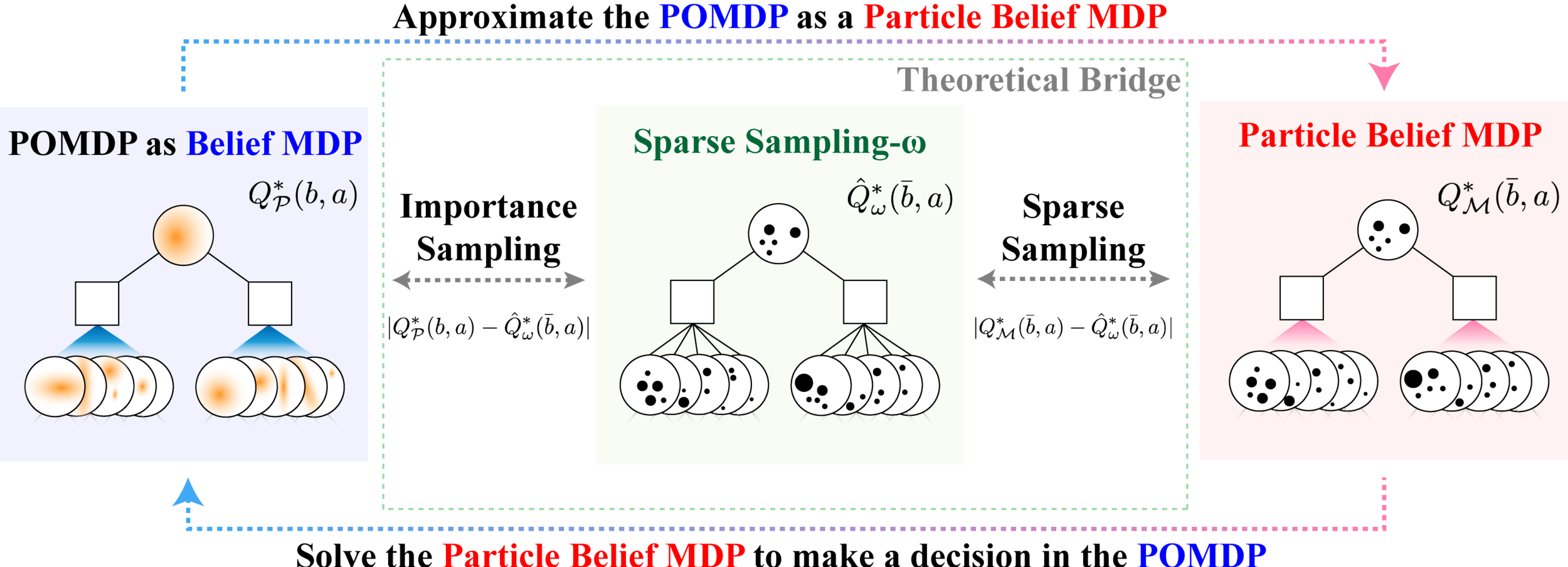
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]

For any \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,

[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]

No direct dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!

Particle belief planning suboptimality

\(C\) is too large for any direct safety guarantees. But, in practice, works extremely well for improving efficiency.

[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]

Why are POMDPs difficult?

  1. Curse of History
  2. Curse of dimensionality
    1. State space
    2. Observation space
    3. Action space

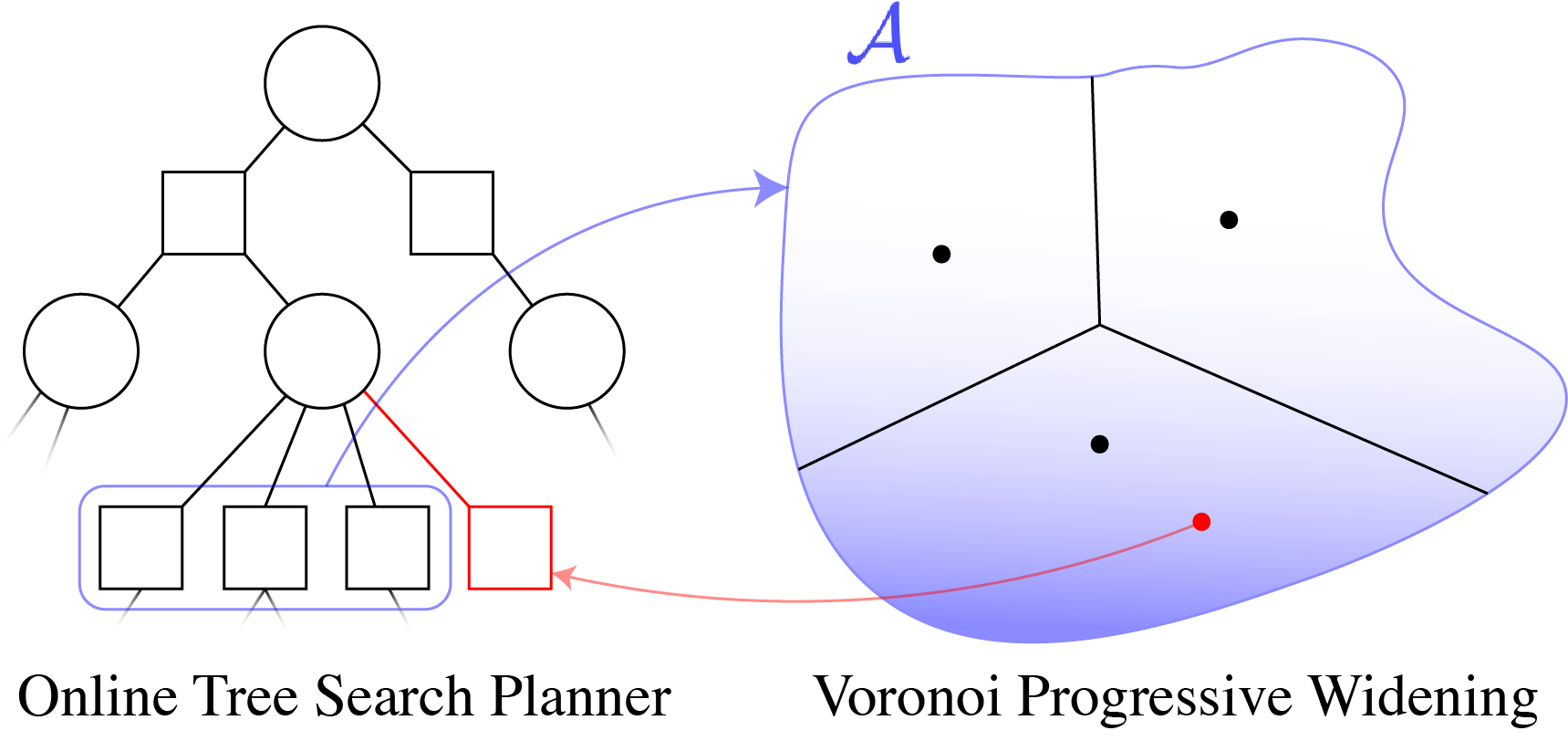
Tree size: \(O\left(\left(|A|C\right)^D\right)\)

Solve simplified surrogate problem for policy deep in the tree

[Lim, Tomlin, and Sunberg, 2021]

Part 3: Steps toward tree search in POSGs

Motivating Example: Laser Tag POMDP

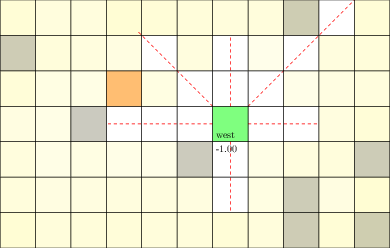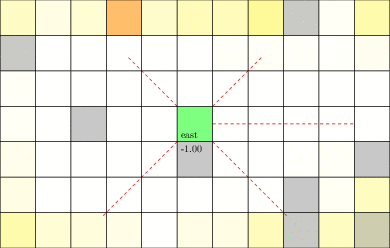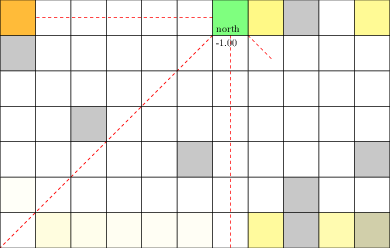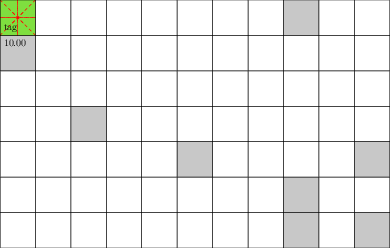
From AlphaZero to POSGs

  1. Simultaneous Play
  2. State Uncertainty
  3. Sufficient Information for Planning
image/svg+xml
image/svg+xml

Policy Network

Value Network

Alpha Zero

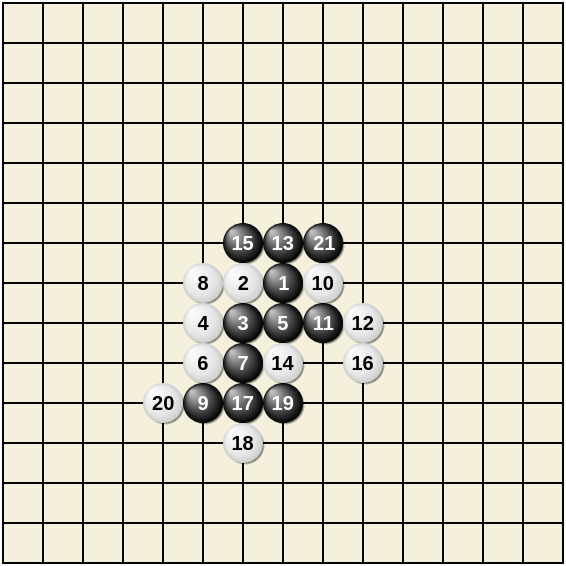
1. Simultaneous Play

1. Exploration

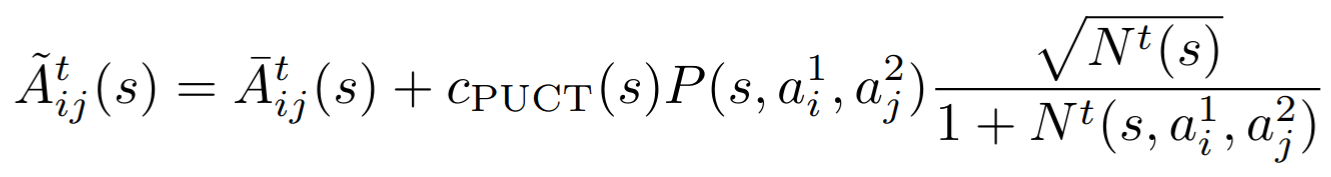
2. Selection

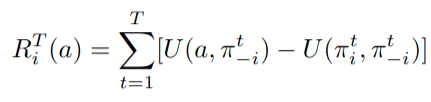
20 steps of regret matching on \(\tilde{A}\)

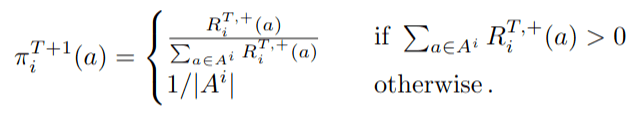
3. Networks

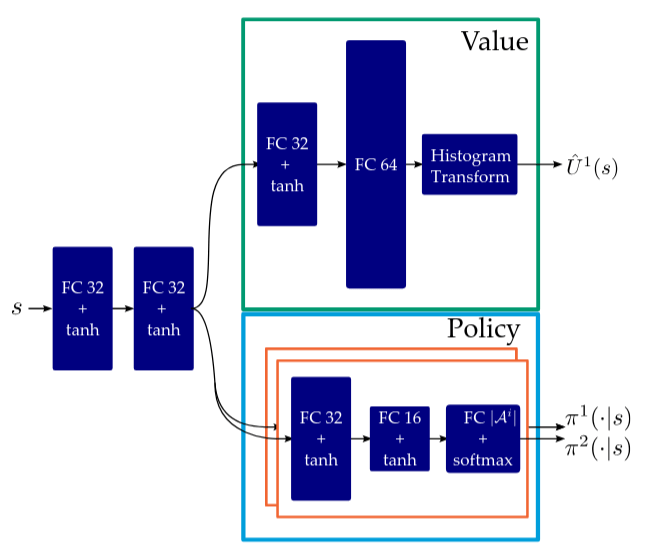
Policy trained to match solution to \(\bar{A}\)

Value distribution trained on sim outcomes

[Becker & Sunberg, AMOS 2025]

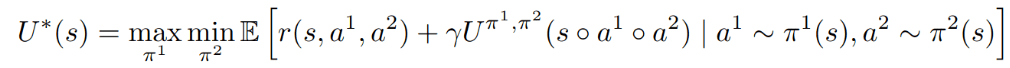
1. Simultaneous Play

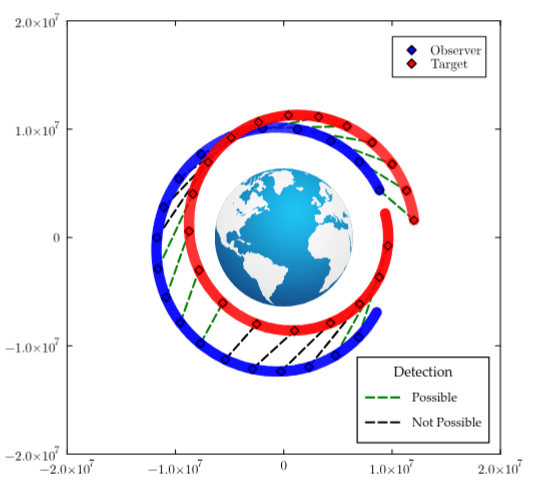
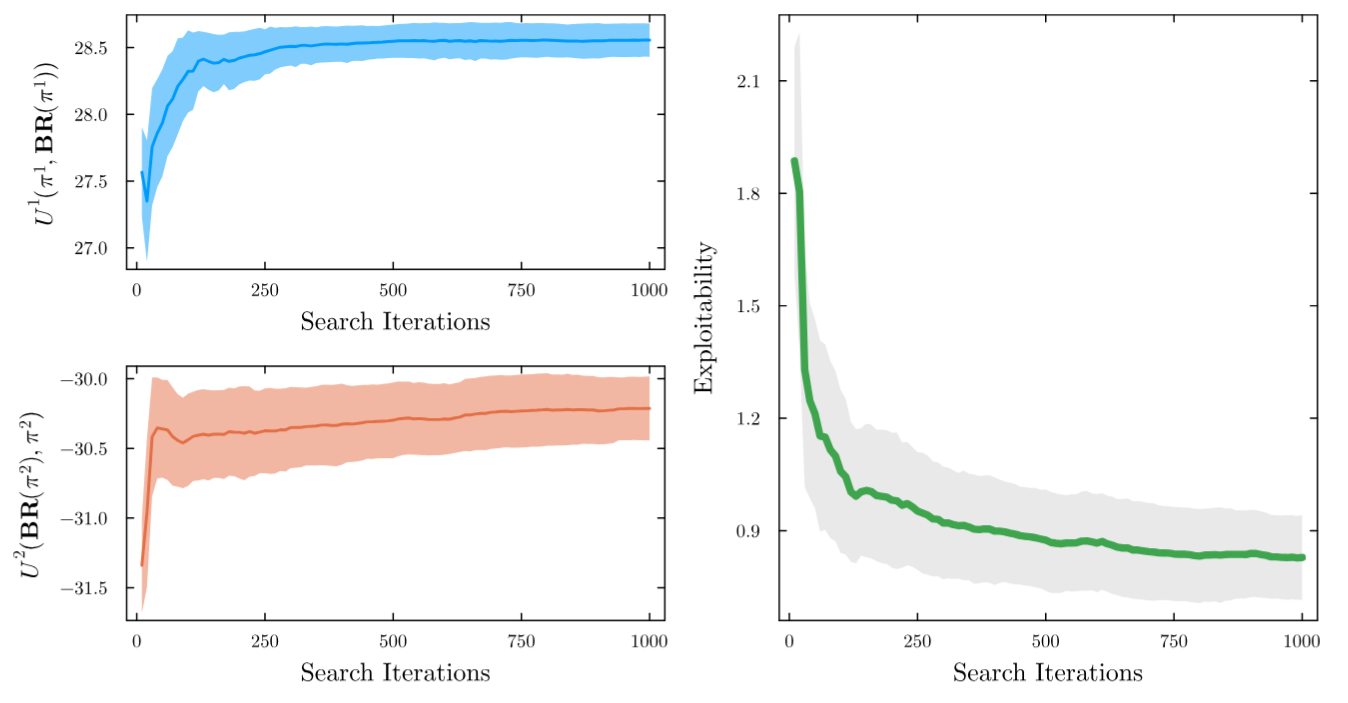
2. Representing State Uncertainty

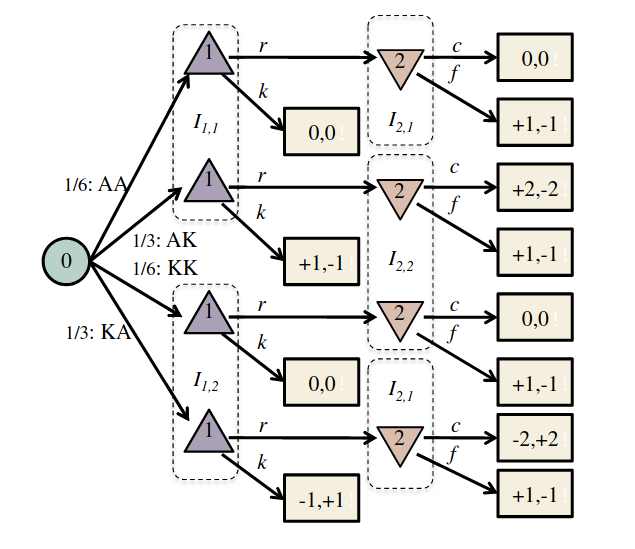
Image: Russel & Norvig, AI, a modern approach

P1: A

P1: K

P2: A

P2: A

P2: K

POMDP

Extensive Form Game

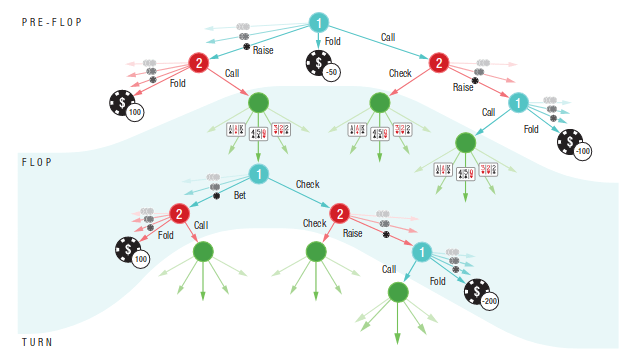
Finding a Nash Equilibrium: Poker

Image: Russel & Norvig, AI, a modern approach

P1: A

P1: K

P2: A

P2: A

P2: K

2. Representing State Uncertainty

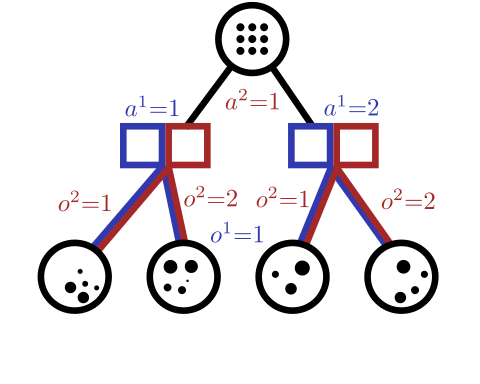
Conditional Distribution InfoSet Tree (CDIT)

Read Martin Schmid's thesis! https://arxiv.org/pdf/2111.05884

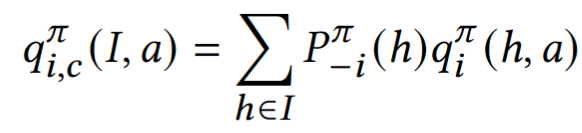
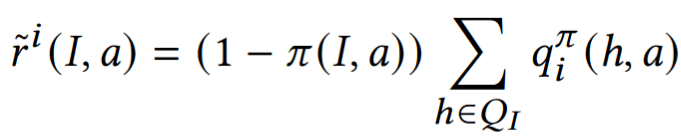
Finding Policies for Zero-Sum Games

Counterfactual Action Utilities

Estimate regret through external sampling

Update policies with regret matching (ESCFR)

2. Representing State Uncertainty

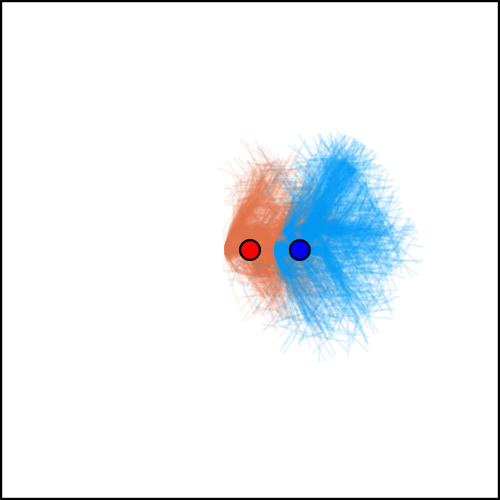
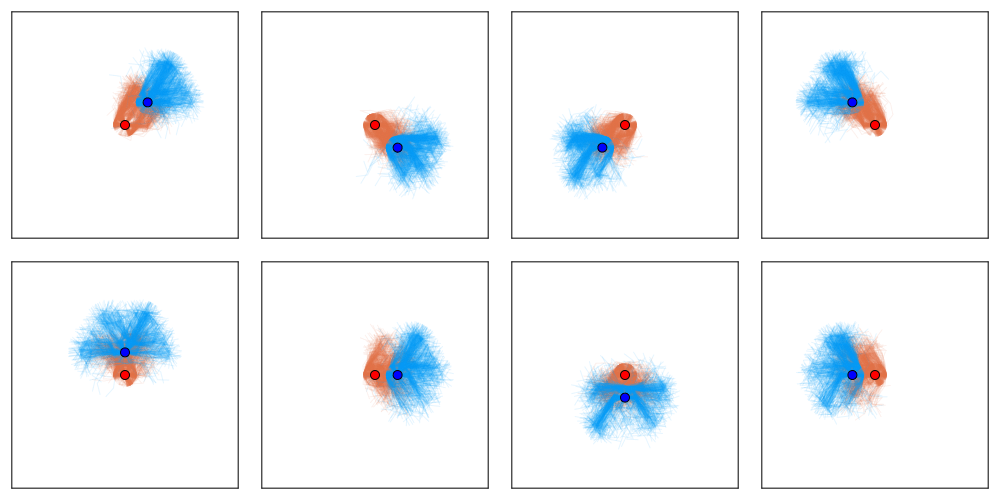
[Becker & Sunberg, AAMAS 2025]

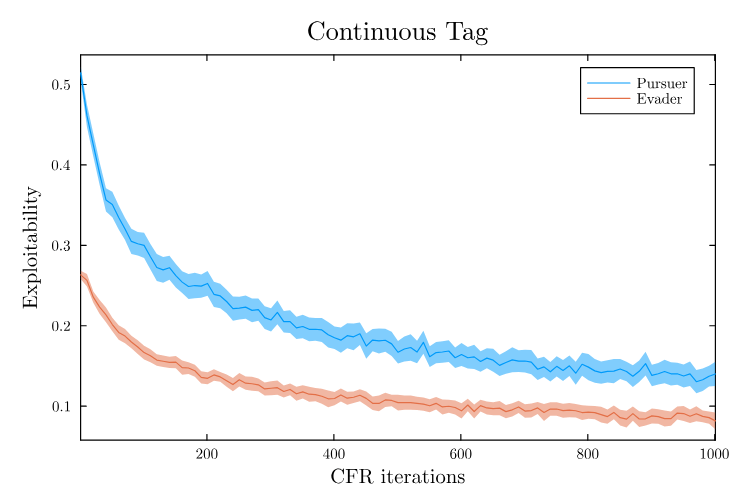
2. Representing State Uncertainty

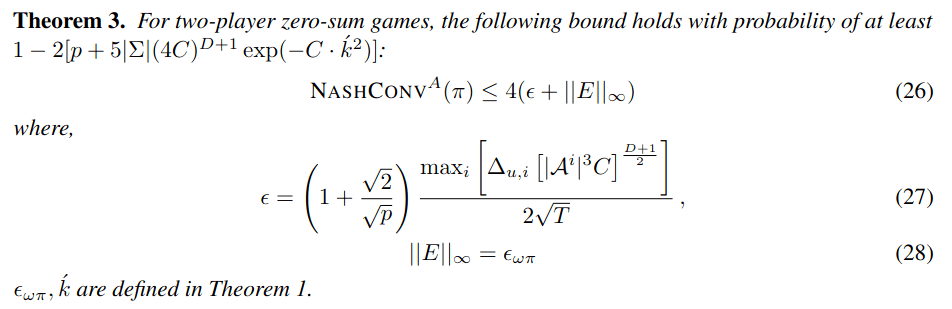
[Becker & Sunberg, AAMAS 2025]

2. Representing State Uncertainty

Will CDITs help solve for the best LaserTag evasion policy?

3. Online Planning

POMDP

POSG

Environment

Belief Updater

Planner

Environment

Planner

P2

What goes here?

Online planning: Is belief enough for games?

How do they solve this in Poker?

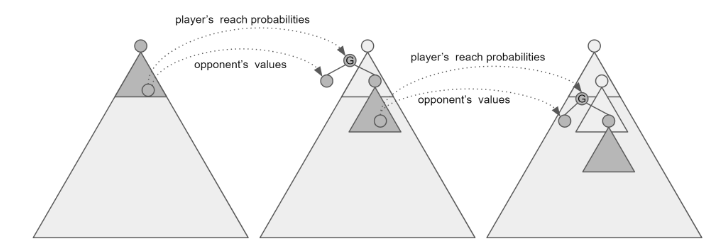
Martin Schmid's thesis: https://arxiv.org/pdf/2111.05884

Thank You!

www.cu-adcl.org

Funding orgs: (all opinions are my own)

VADeR

Autonomous Decision and Control Laboratory

cu-adcl.org

  • Algorithmic Contributions
    • Scalable algorithms for partially observable Markov decision processes (POMDPs)
    • Motion planning with safety guarantees
    • Game theoretic algorithms
  • Theoretical Contributions
    • Particle POMDP approximation bounds
  • Applications
    • Space Domain Awareness
    • Autonomous Driving
    • Autonomous Aerial Scientific Missions
    • Search and Rescue
    • Space Exploration
    • Ecology
  • Open Source Software
    • POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students

Postdoc