Safe and efficient autonomy in the face of state and interaction uncertainty
Professor Zachary Sunberg
May 12th, 2022
Mission: deploy autonomy with confidence


Waymo Image By Dllu - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=64517567



Two Objectives for Autonomy
EFFICIENCY
SAFETY
Minimize resource use
(especially time)
Minimize the risk of harm to oneself and others

Safety often opposes Efficiency

Tweet by Nitin Gupta
29 April 2018
https://twitter.com/nitguptaa/status/990683818825736192
Pareto Optimization
Safety
Better Performance
Model \(M_2\), Algorithm \(A_2\)
Model \(M_1\), Algorithm \(A_1\)
Efficiency
$$\underset{\pi}{\mathop{\text{maximize}}} \, V^\pi = V^\pi_\text{E} + \lambda V^\pi_\text{S}$$
Safety
Weight
Efficiency

Types of Uncertainty
Alleatory
Epistemic (Static)
Epistemic (Dynamic)


Interaction

MDP

RL
POMDP
Game
Markov Decision Process (MDP)
- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Alleatory
Partially Observable Markov Decision Process (POMDP)

- \(\mathcal{S}\) - State space
- \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
- \(\mathcal{A}\) - Action space
- \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
- \(\mathcal{O}\) - Observation space
- \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution
Alleatory
Epistemic (Static)
Epistemic (Dynamic)
Incomplete Information Game
Alleatory
Epistemic (Static)
Epistemic (Dynamic)
Interaction

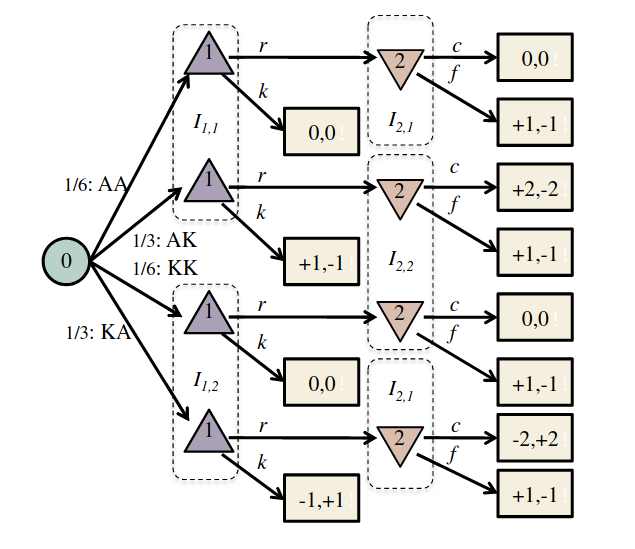
- Finite set of \(n\) players, plus the "chance" player
- \(P(h)\) (player at each history)
- \(A(h)\) (set of actions at each history)
- \(I(h)\) (information set that each history maps to)
- \(U(h)\) (payoff for each leaf node in the game tree)
Image from Russel and Norvig
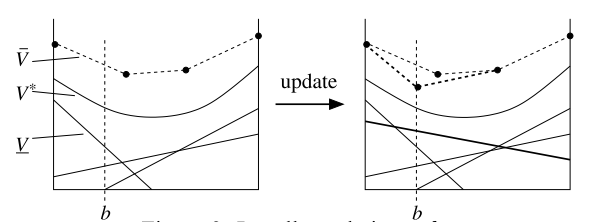
Solving MDPs - The Value Function
$$V^*(s) = \underset{a\in\mathcal{A}}{\max} \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$
Involves all future time
Involves only \(t\) and \(t+1\)
$$\underset{\pi:\, \mathcal{S}\to\mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, \pi(s_t)) \bigm| s_0 = s \right]$$
$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$
Value = expected sum of future rewards
Value Iteration
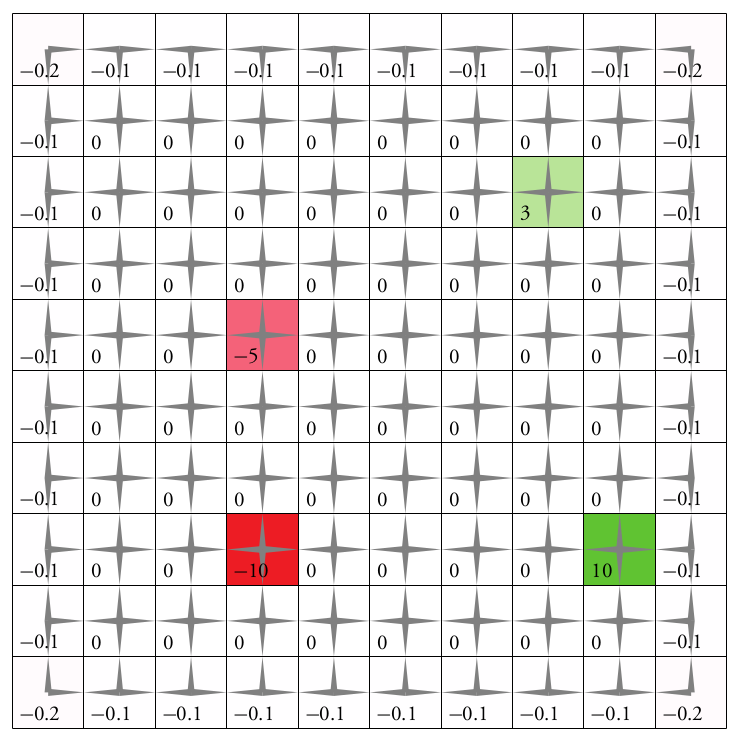
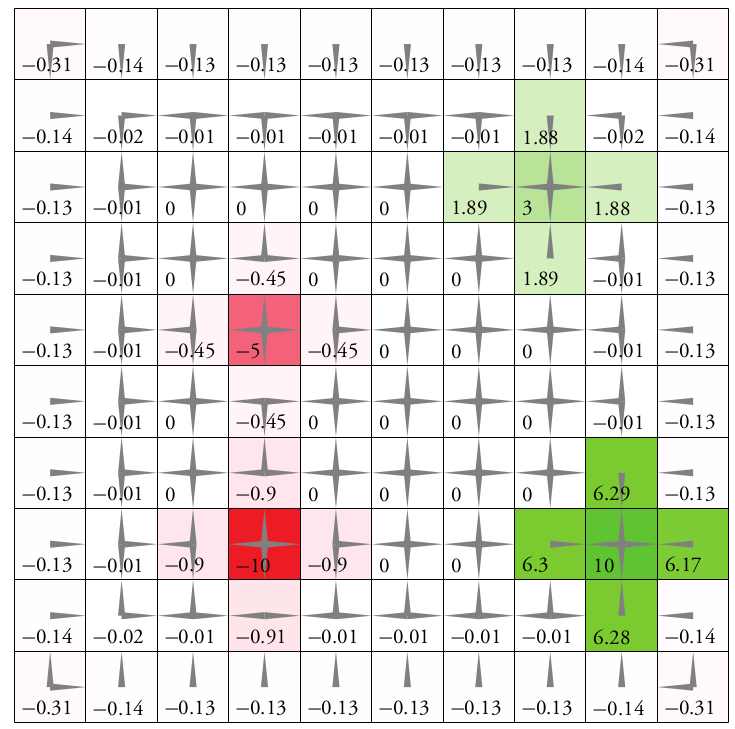
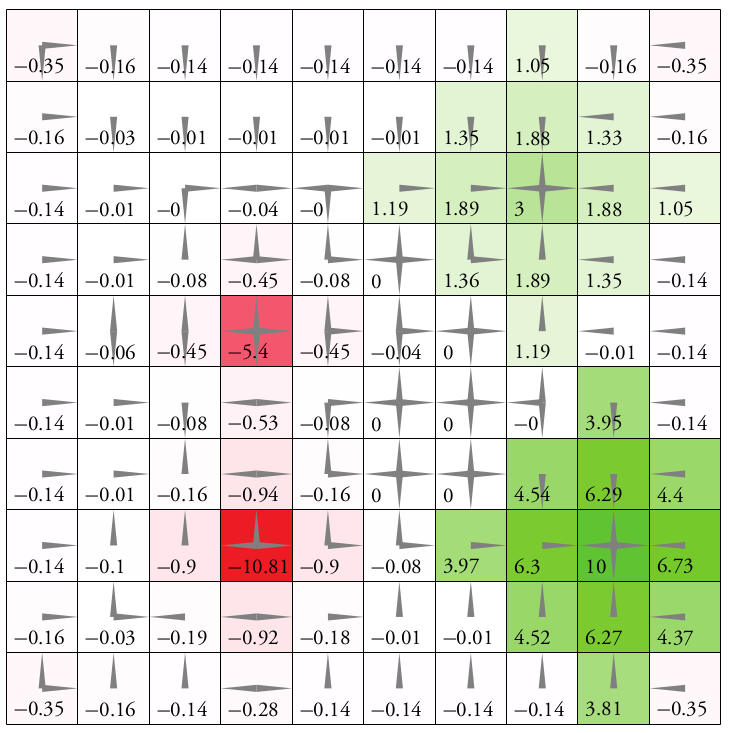
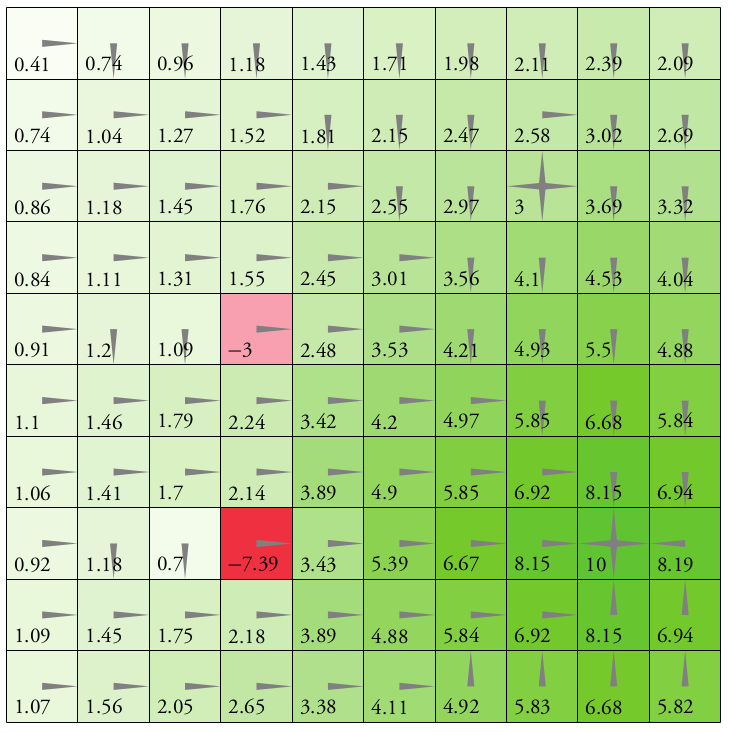

State
Timestep
Accurate Observations
Goal: \(a=0\) at \(s=0\)
Optimal Policy
Localize
\(a=0\)
POMDP Example: Light-Dark
POMDP Sense-Plan-Act Loop
Environment
Belief Updater
Policy/Planner
\(b\)
\(a\)
\[b_t(s) = P\left(s_t = s \mid a_1, o_1 \ldots a_{t-1}, o_{t-1}\right)\]



True State
\(s = 7\)
Observation \(o = -0.21\)
A POMDP is an MDP on the Belief Space
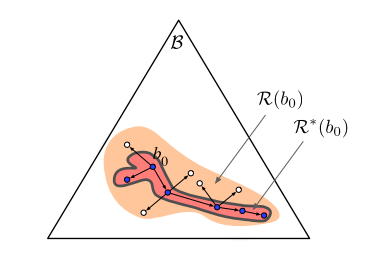
SARSOP can solve some POMDPs with thousands of states offline
but
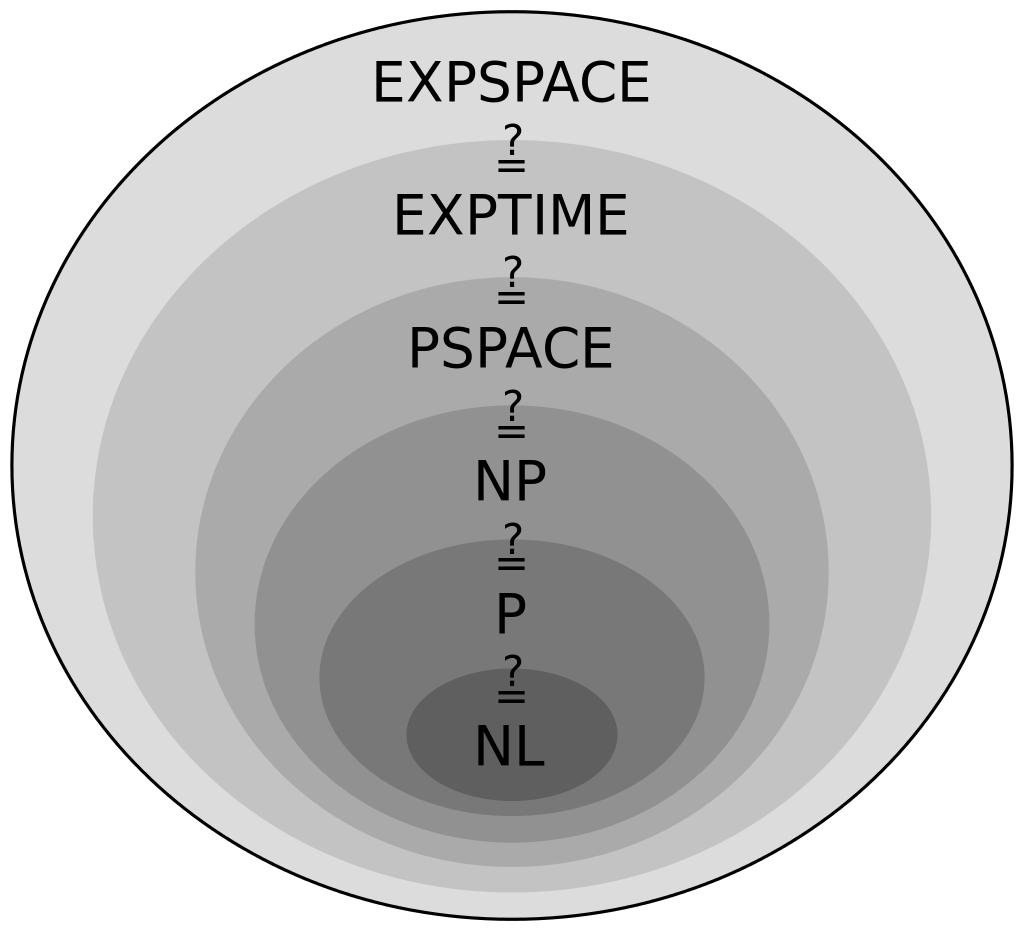
The POMDP is PSPACE-Complete
Intractable!
Online Tree Search in MDPs

Time
Estimate \(Q(s, a)\) based on children
$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$

\[V(s) = \max_a Q(s,a)\]
Sparse Sampling
Expand for all actions (\(\left|\mathcal{A}\right| = 2\) in this case)
...
Expand for all \(\left|\mathcal{S}\right|\) states
\(C=3\) states
Sparse Sampling
...
[Kearns, et al., 2002]
1. Near-optimal policy: \(\left|V^A(s) - V^*(s) \right|\leq \epsilon\)
2. Running time independent of state space size:
\(O \left( ( \left|\mathcal{A} \right|C )^H \right) \)
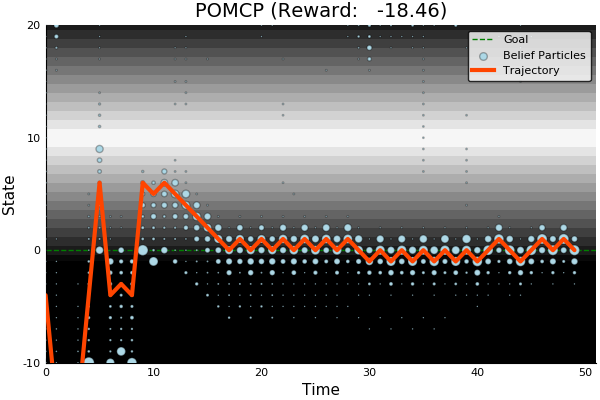
- A POMDP is an MDP on the Belief Space but belief updates are expensive
- POMCP* uses simulations of histories instead of full belief updates
- Each belief is implicitly represented by a collection of unweighted particles


[Ross, 2008] [Silver, 2010]
*(Partially Observable Monte Carlo Planning)
Fails in Continuous Observation Spaces
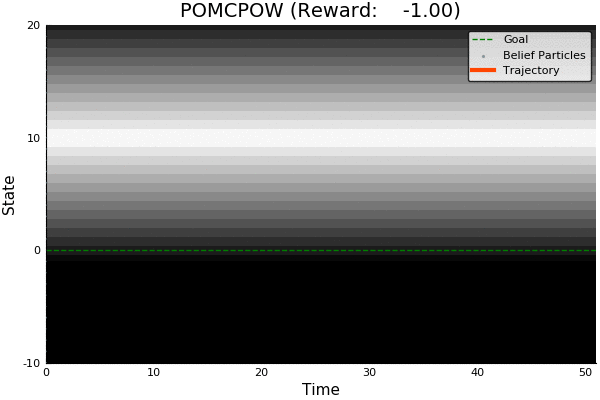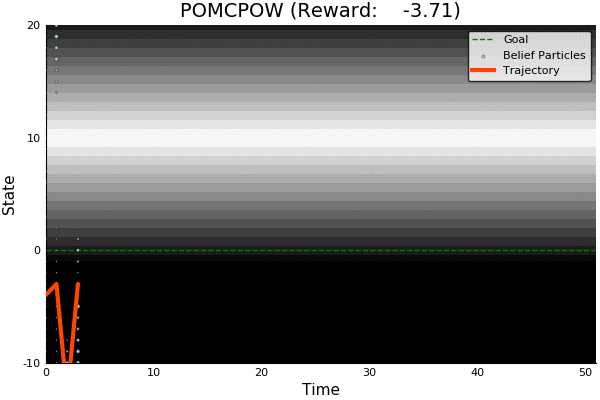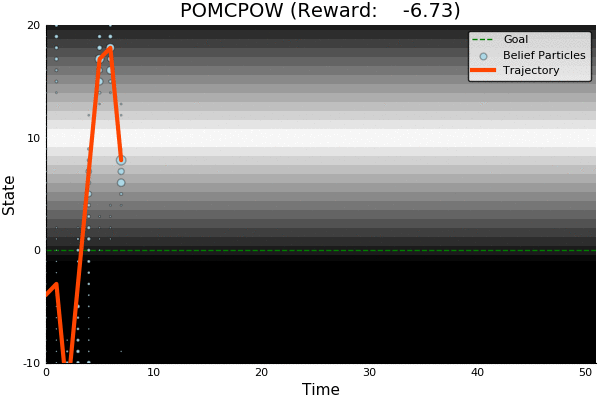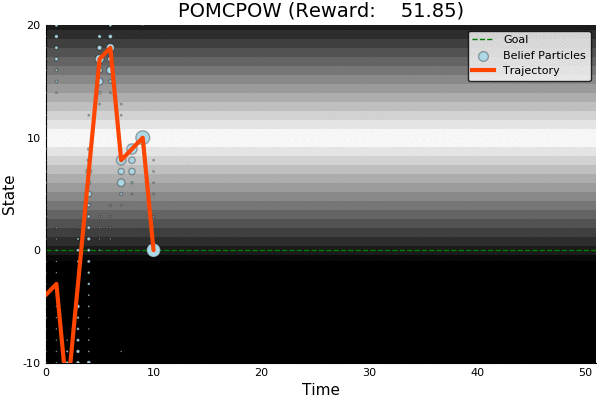



POMCP
POMCP-DPW
POMCPOW
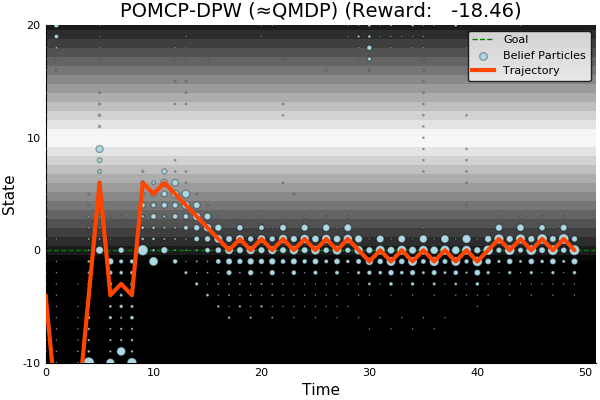
[Sunberg and Kochenderfer, ICAPS 2018]







MDP trained on normal drivers



MDP trained on all drivers
Omniscient
POMCPOW (Ours)
Simulation results
[Sunberg & Kochenderfer, T-ITS Under Review]
Continuous Observation Analytical Results (POWSS)


Our simplified algorithm is near-optimal
[Lim, Tomlin, & Sunberg, IJCAI 2020]

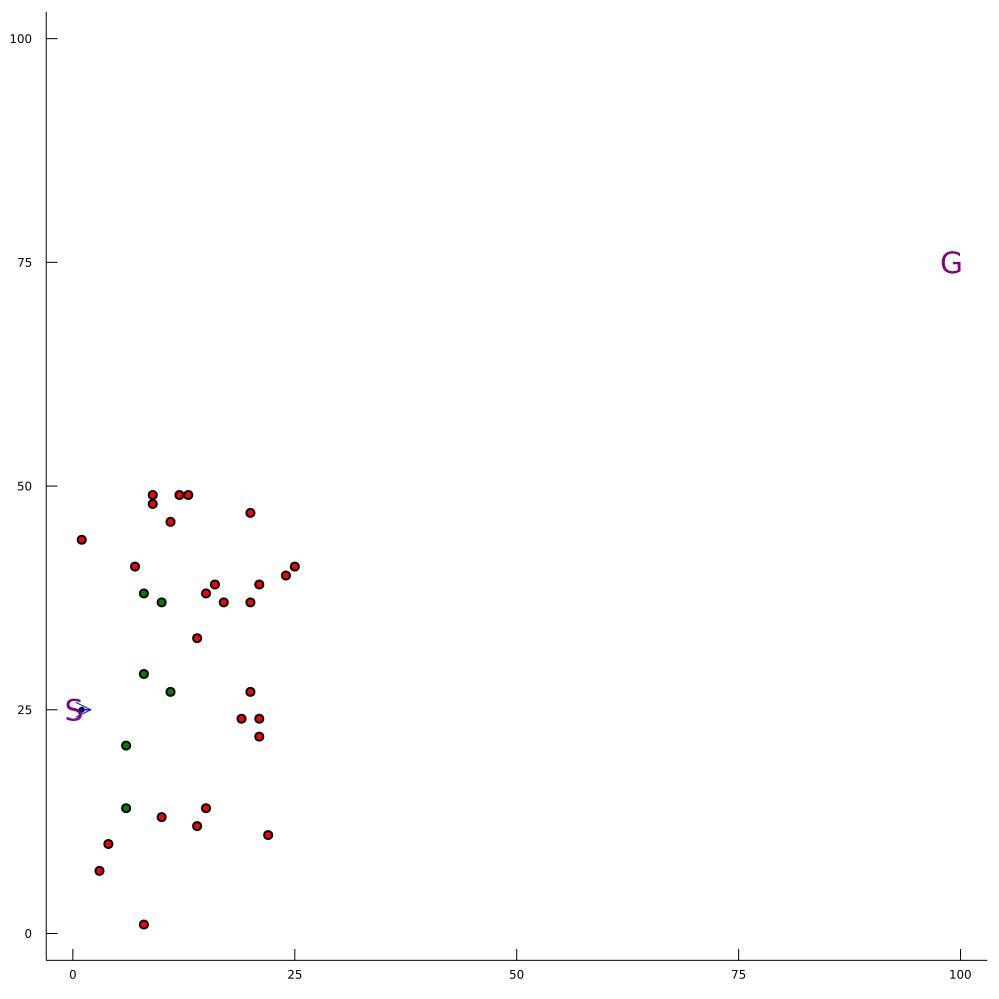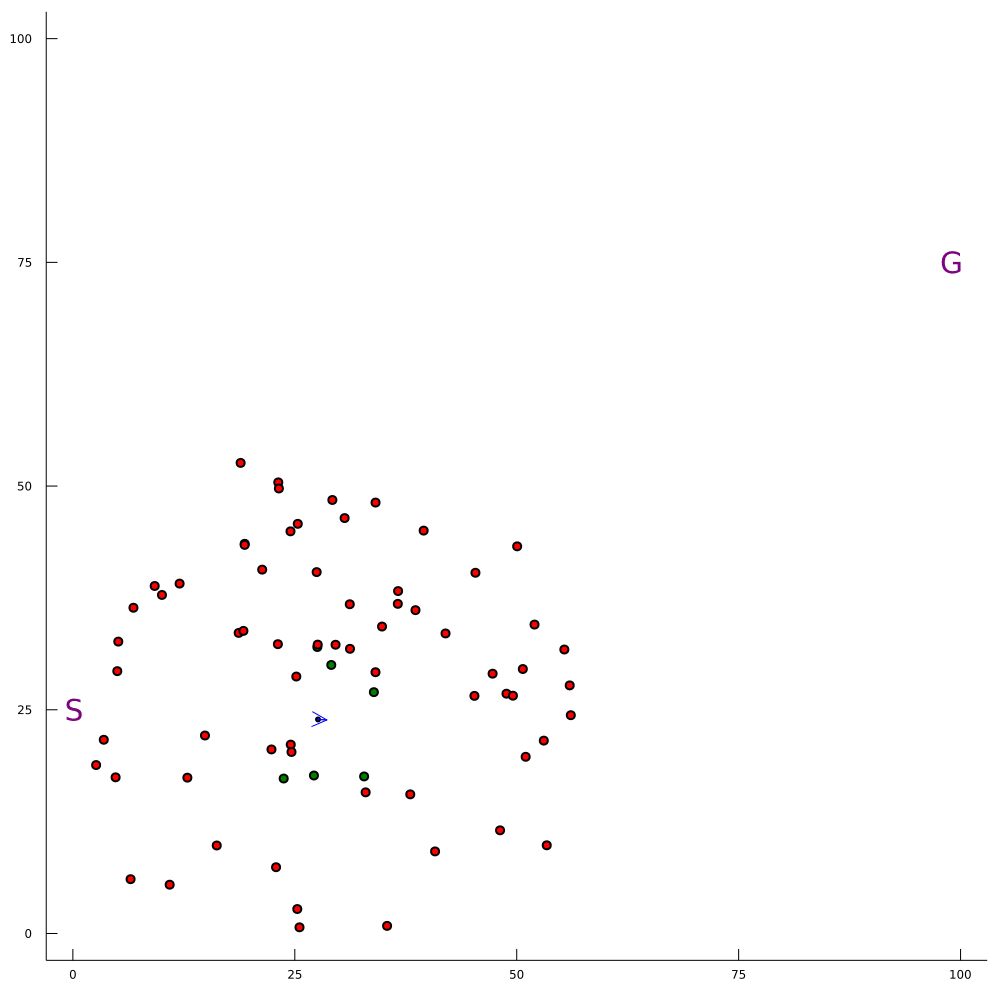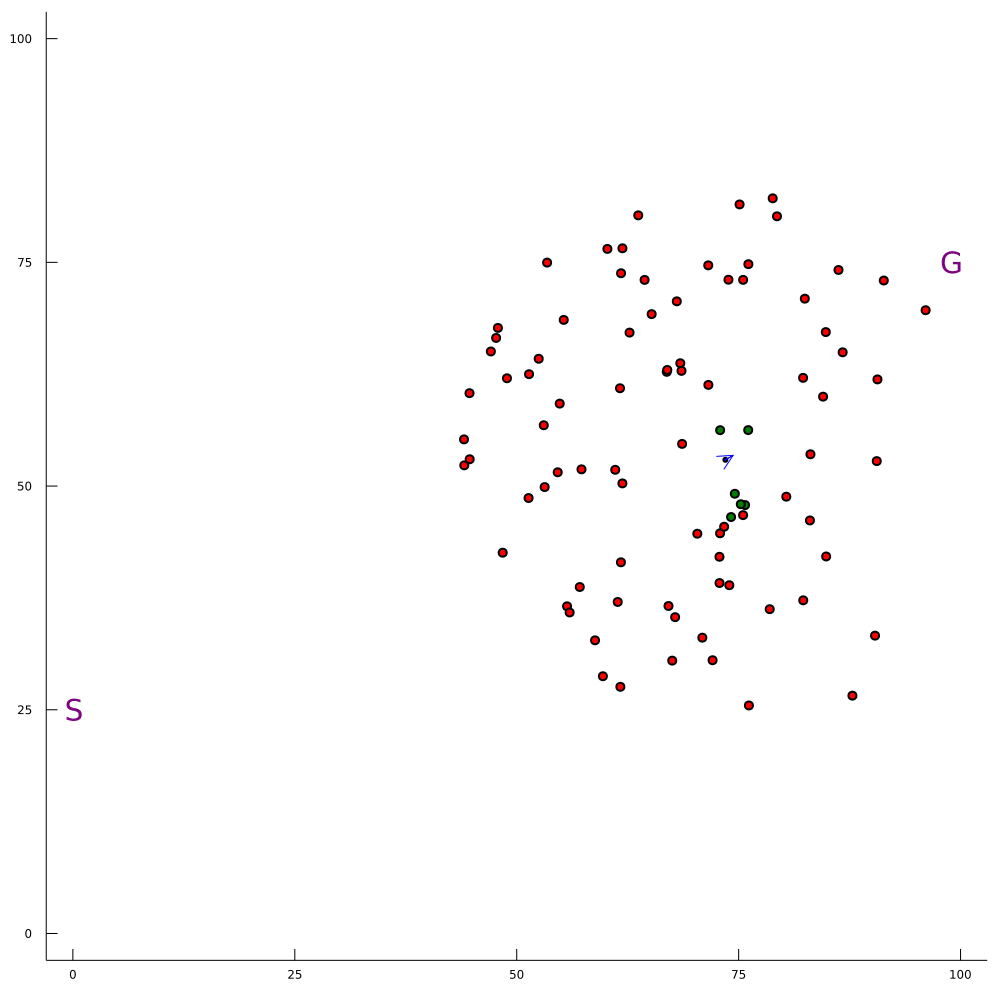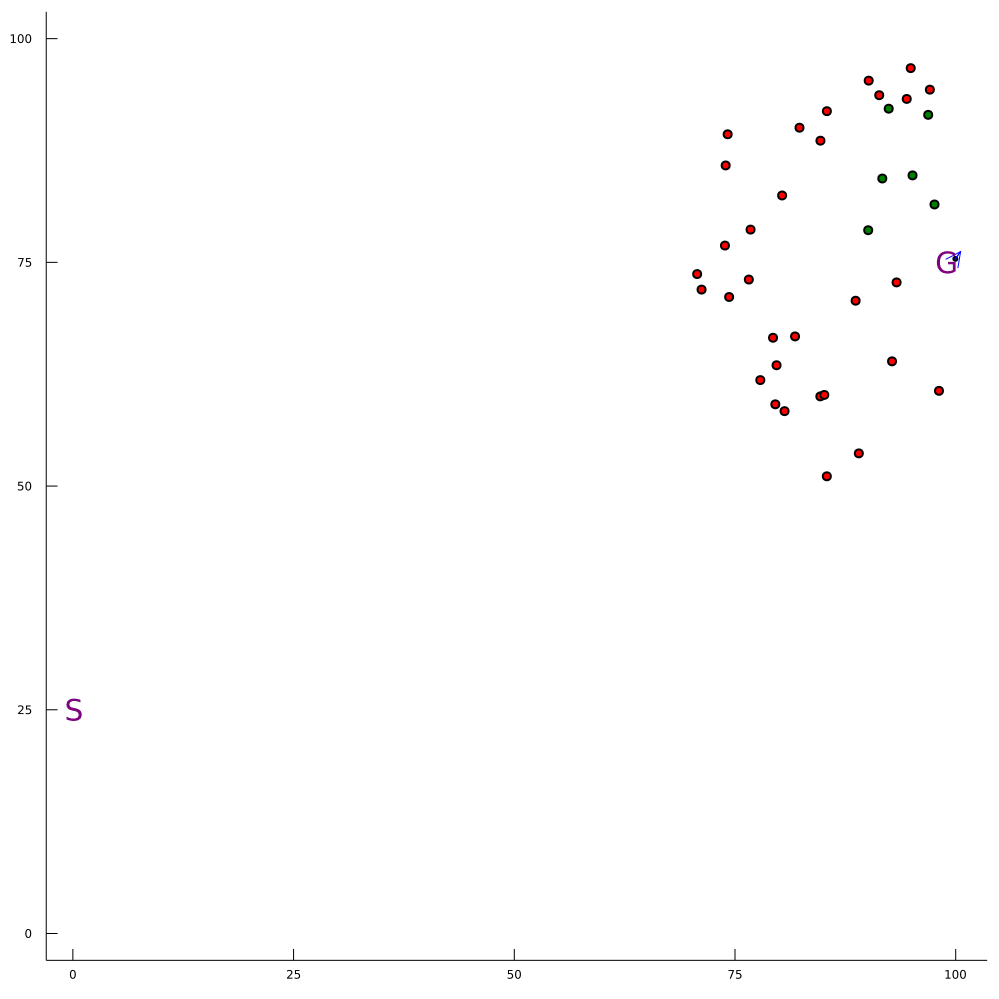
Conventional 1D POMDP
2D POMDP

Pedestrian Navigation



Intention-Aware Navigation in Crowds with Extended-Space POMDP Planning. Gupta, H.; Hayes, B.; and Sunberg, Z. AAMAS, 2022.


POMDP Planning with Image Observations



Actions
Observations
States
POMDPs with Continuous...
- PO-UCT (POMCP)
- DESPOT
- POMCPOW
- DESPOT-α
- LABECOP
- Ada-OPS
- GPS-ABT
- VG-MCTS
- BOMCP
- VOMCPOW
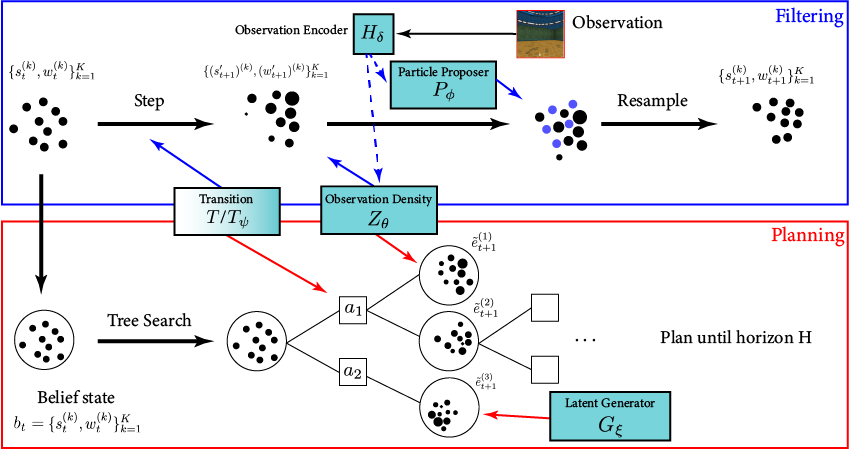
BOMCP


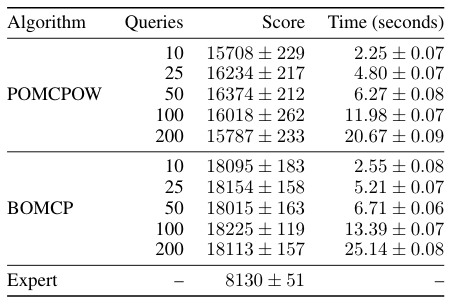
[Mern, Sunberg, et al. AAAI 2021]
Voronoi Progressive Widening
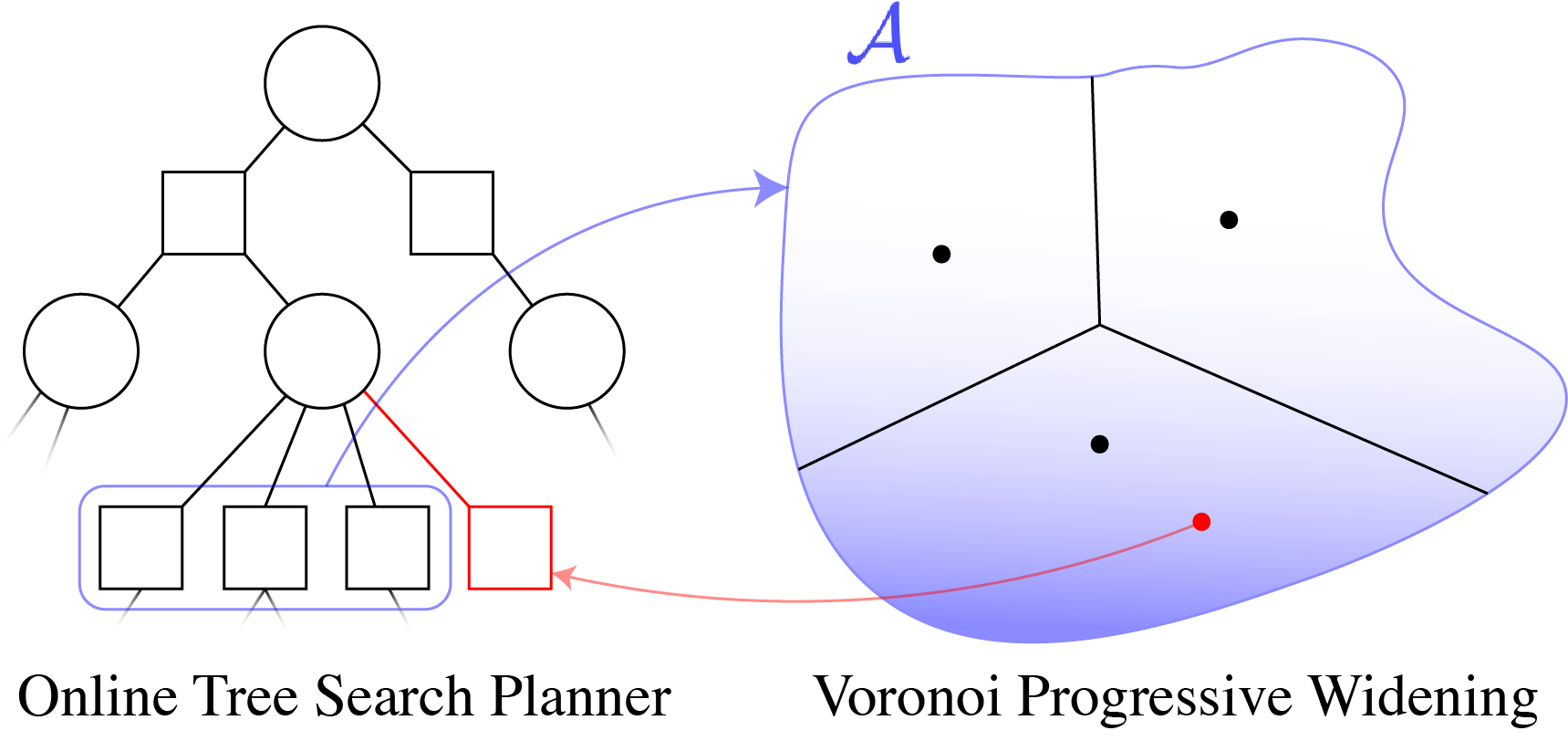
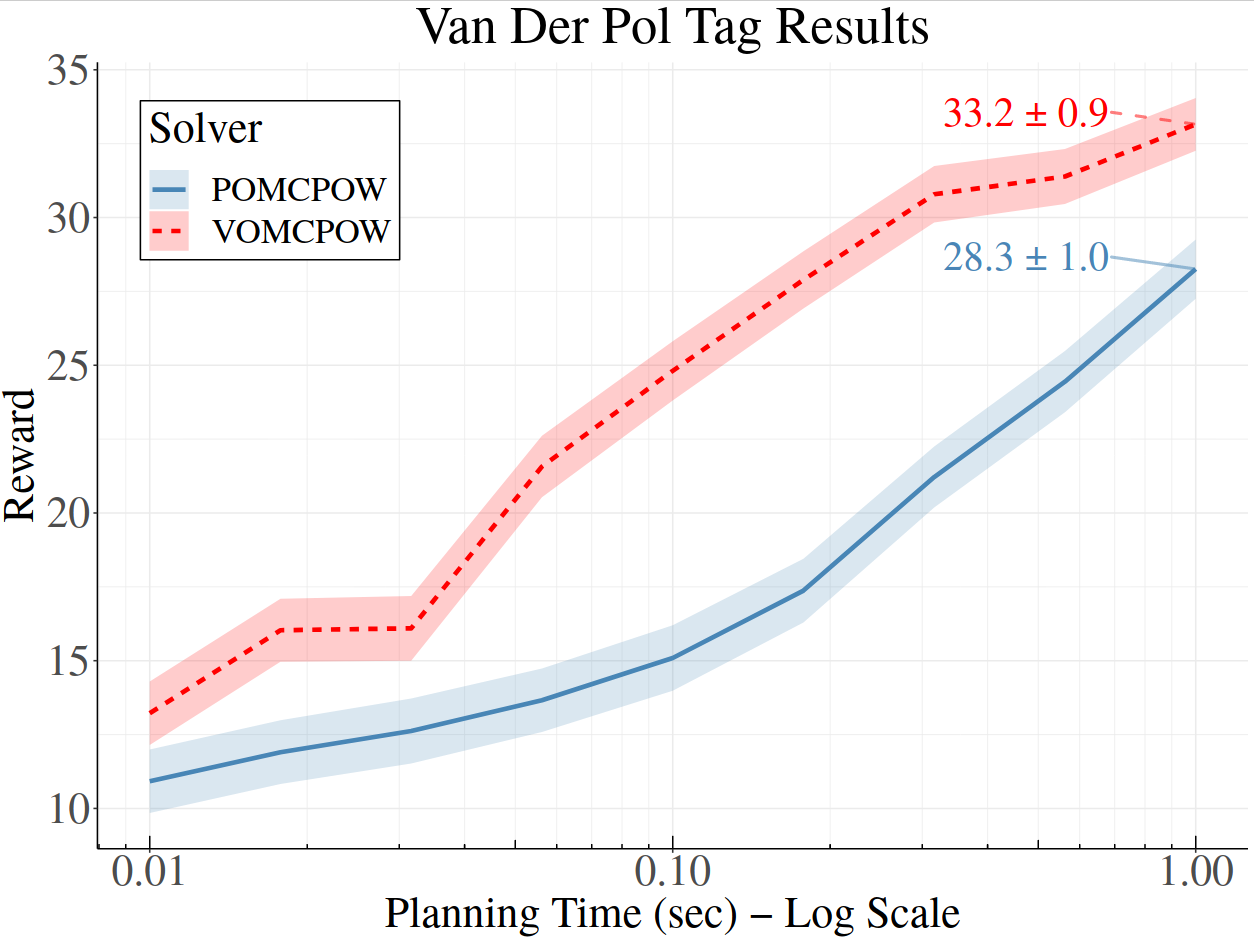

[Lim, Tomlin, & Sunberg CDC 2021]
Games
Interaction Uncertainty

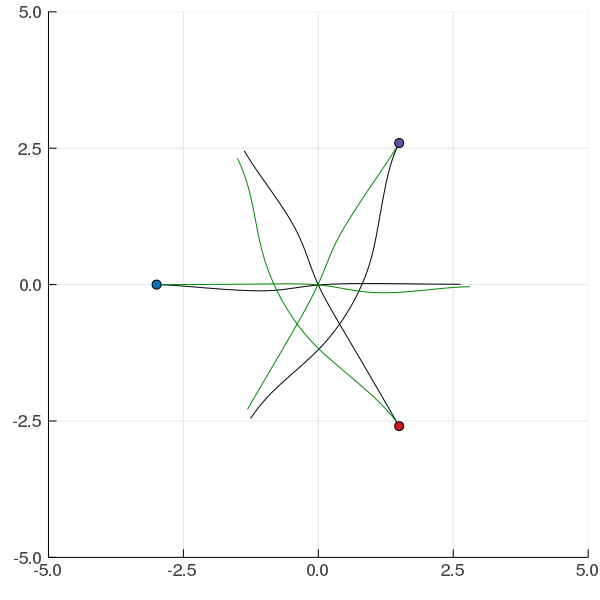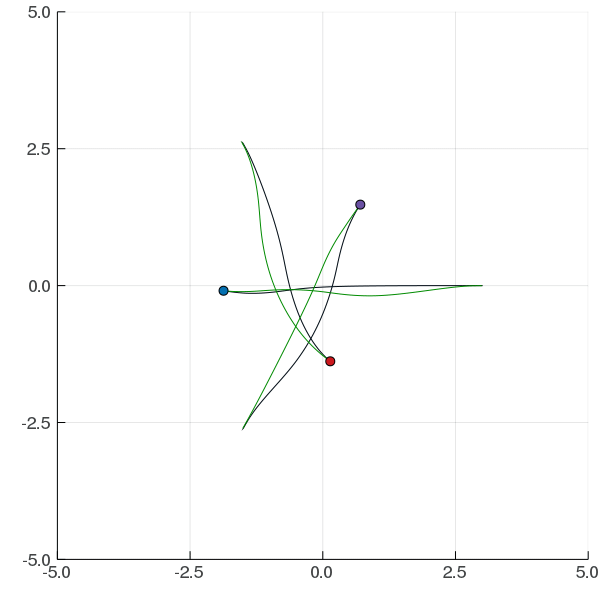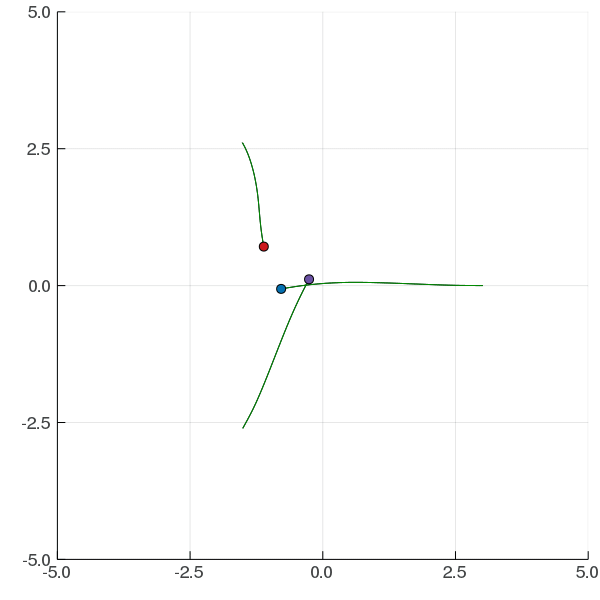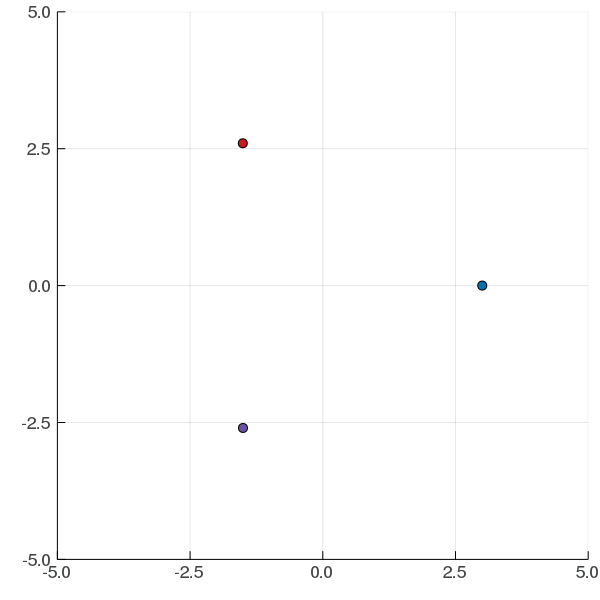
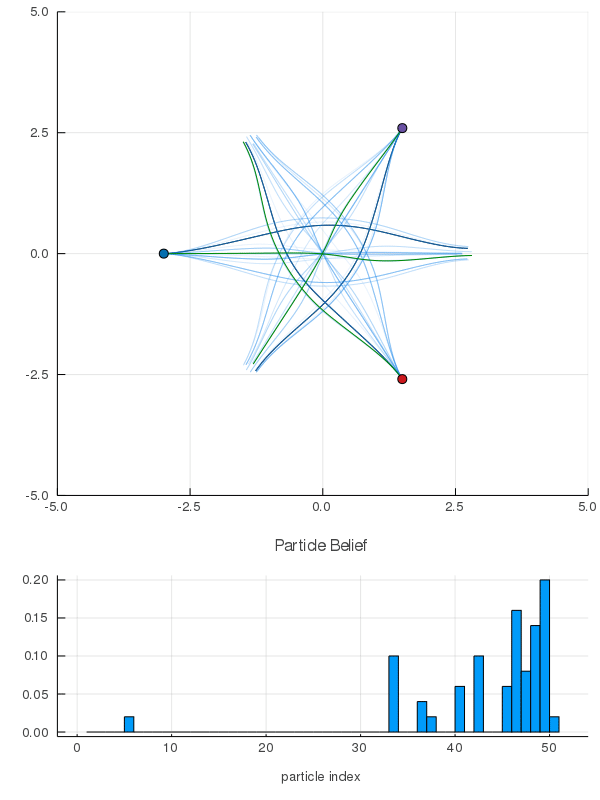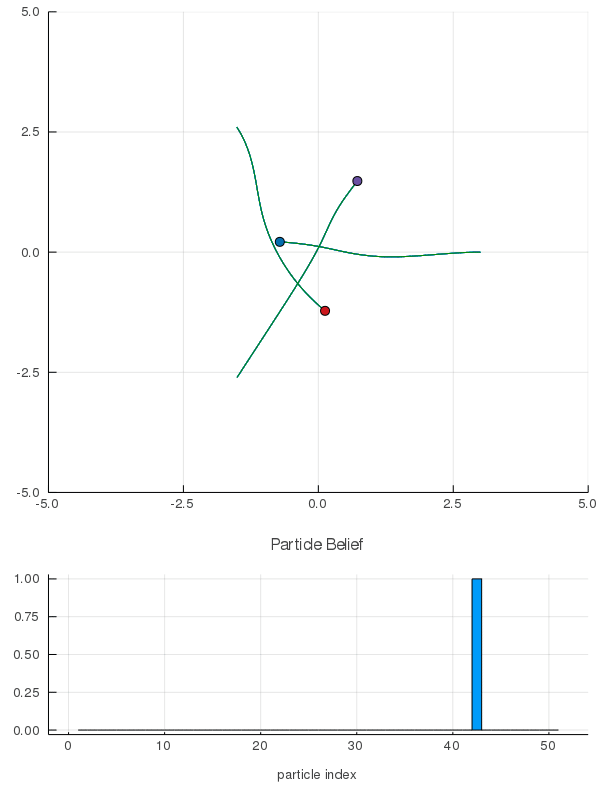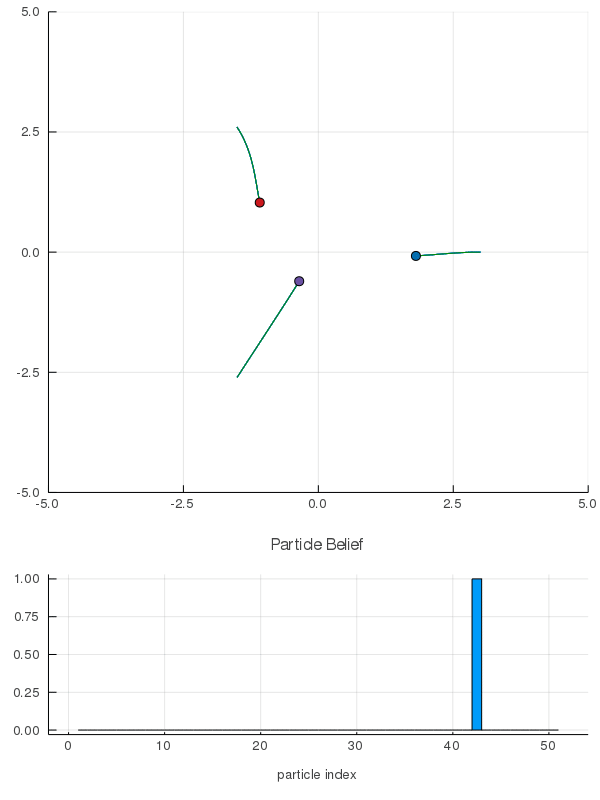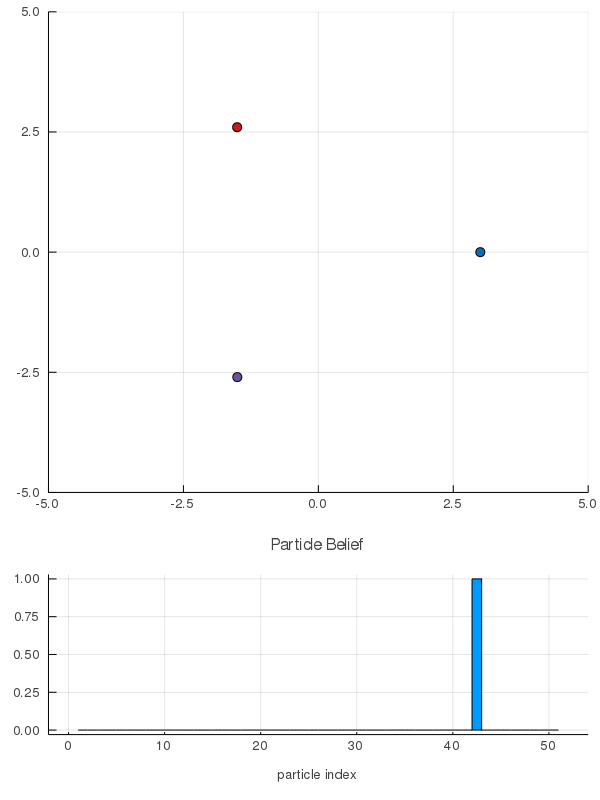

[Peters, Tomlin, and Sunberg 2020]
Space Domain Awareness Games

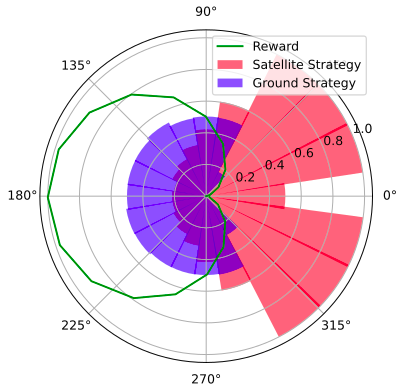

1
2
...
...
...
...
...
...
...
\(N\)
Tyler Becker and Zachary Sunberg. “Imperfect Information Games and Counterfac-
tual Regret Minimization in Space Domain Awareness”. Abstract under review for the
Advanced Maui Optical and Space Surveillance Technologies conference.
Open Source Software
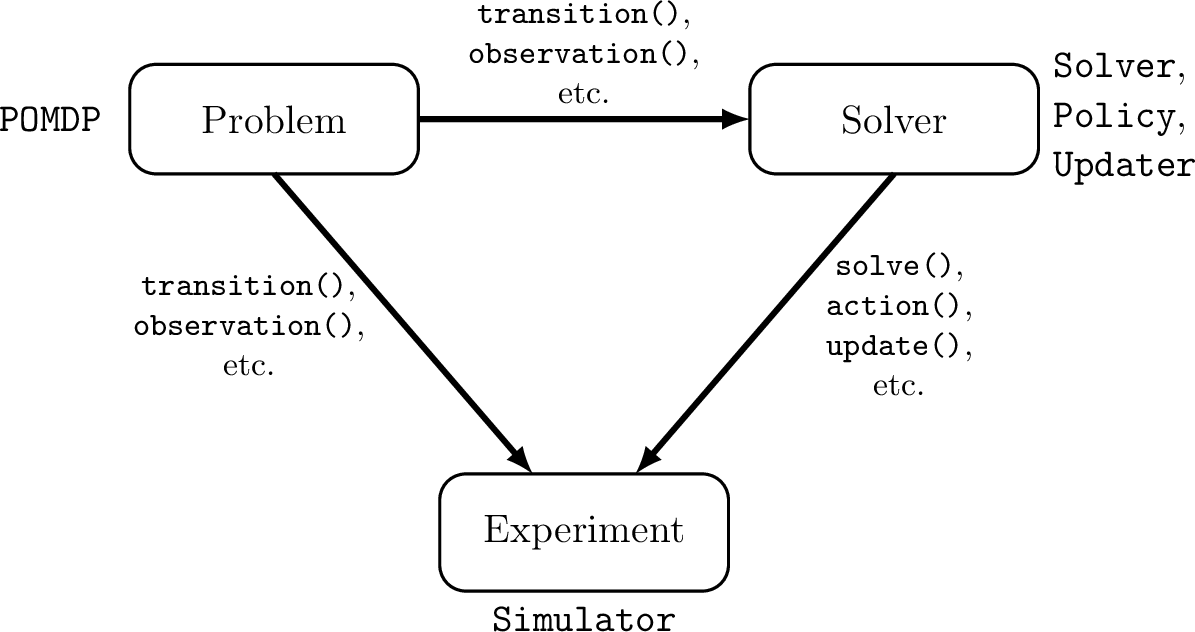

POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia
Challenges for POMDP Software
- There is a huge variety of
- Problems
- Continuous/Discrete
- Fully/Partially Observable
- Generative/Explicit
- Simple/Complex
- Solvers
- Online/Offline
- Alpha Vector/Graph/Tree
- Exact/Approximate
- Domain-specific heuristics
- Problems
- POMDPs are computationally difficult.
Explicit
Black Box
("Generative" in POMDP lit.)

\(s,a\)
\(s', o, r\)
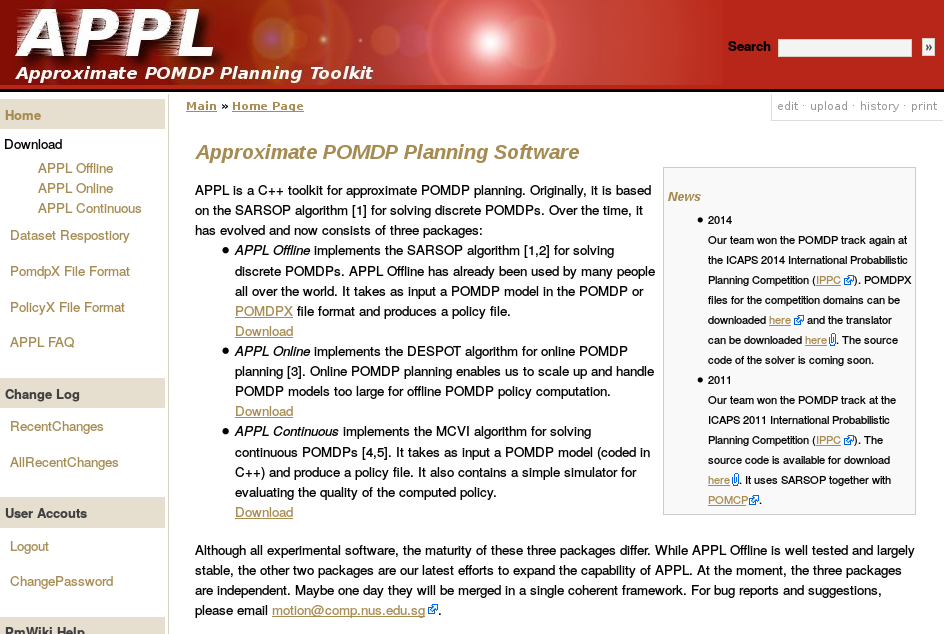
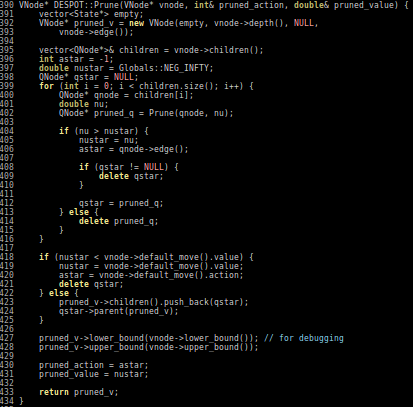
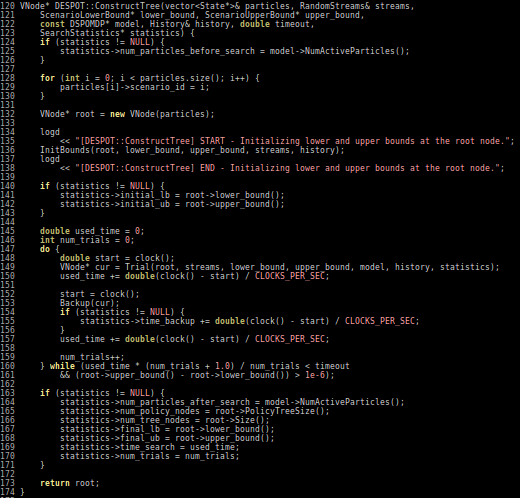
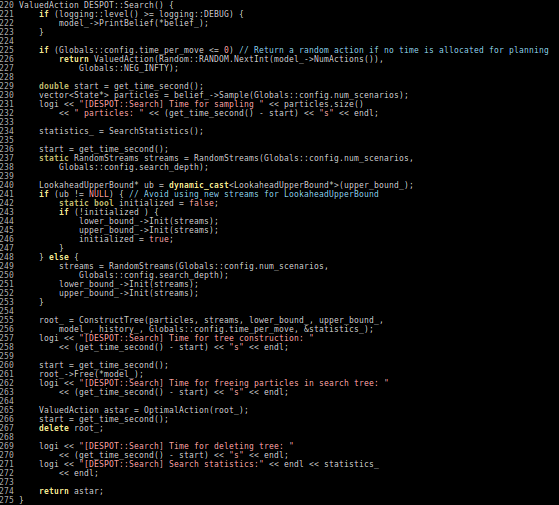
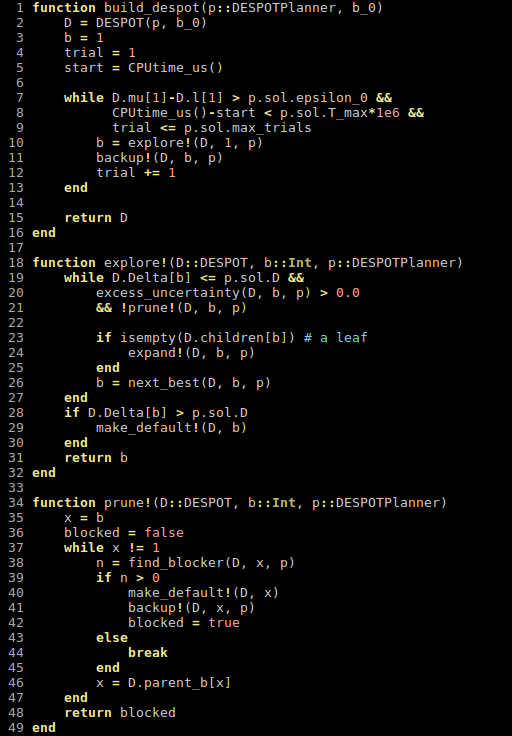
Previous C++ framework: APPL
"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."






Julia - Speed

Celeste Project
1.54 Petaflops

Group








Thank You!

Recent and Current Projects
COVID POMDP
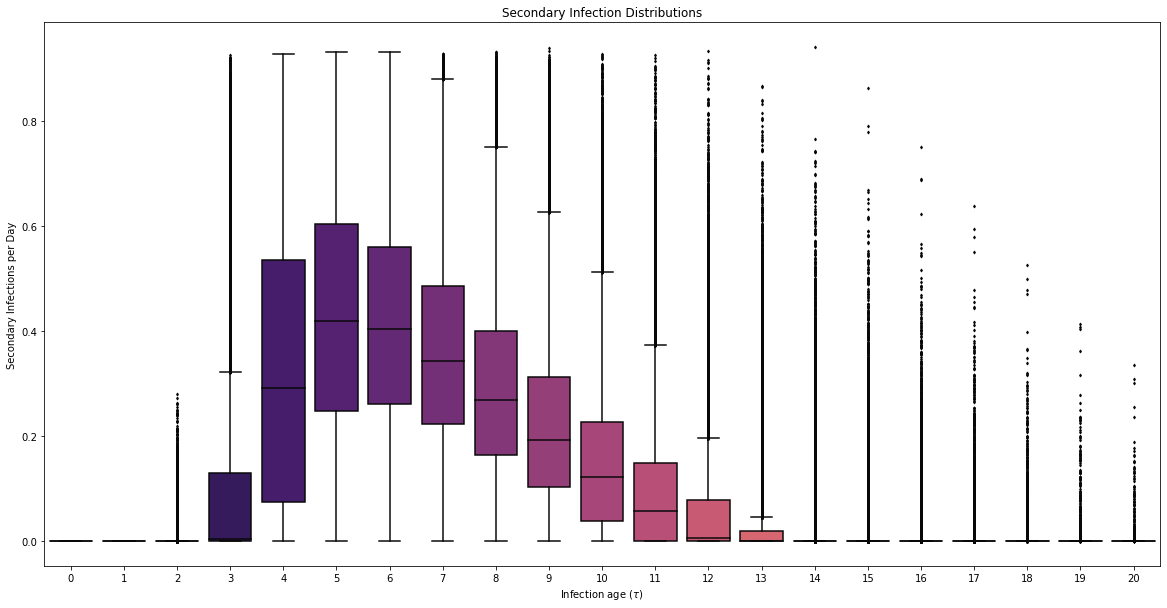
Individual Infectiousness
Infection Age
Incident Infections

Need
Test sensitivity is secondary to frequency and turnaround time for COVID-19 surveillance
Larremore et al.
Viral load represented by piecewise-linear hinge function


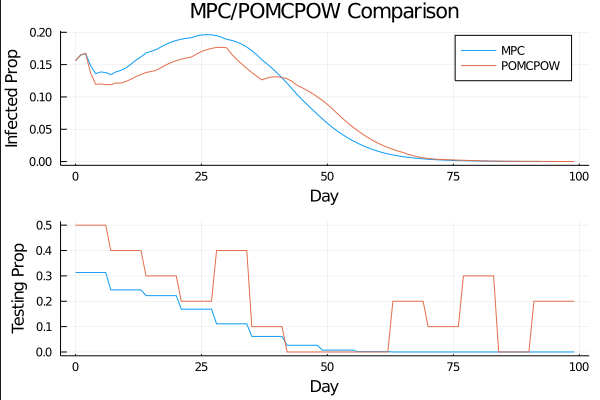
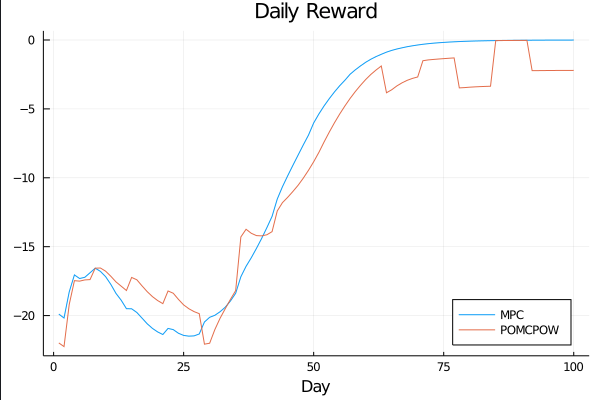
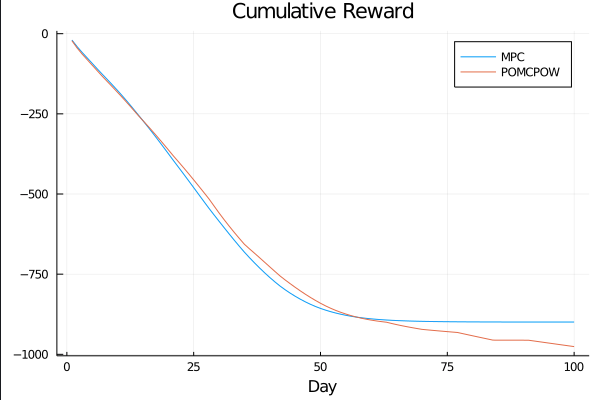

Sparse PFT
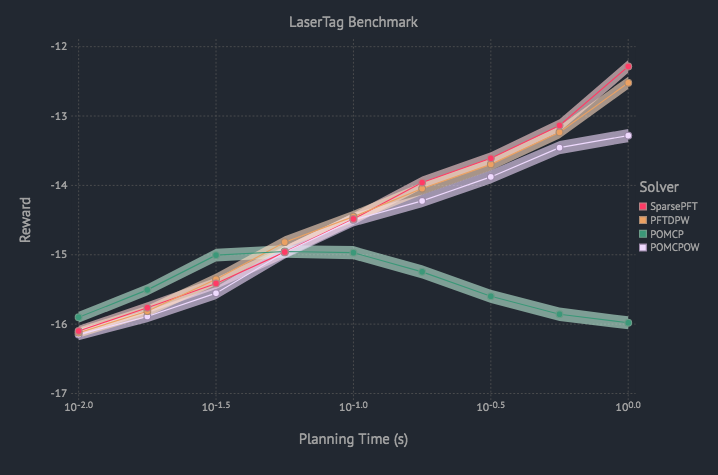


Active Information Gathering for Safety
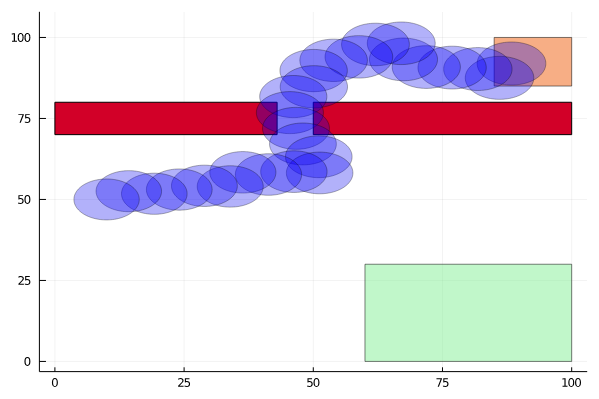
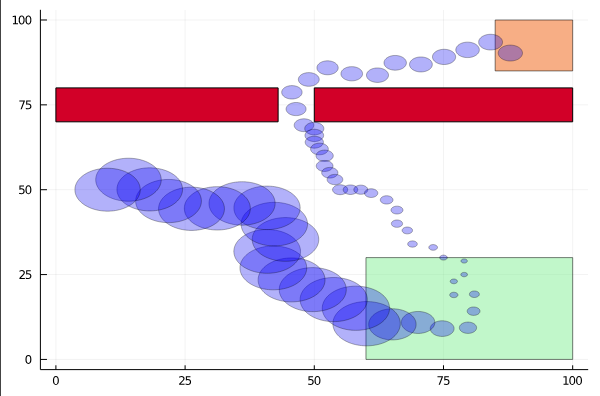


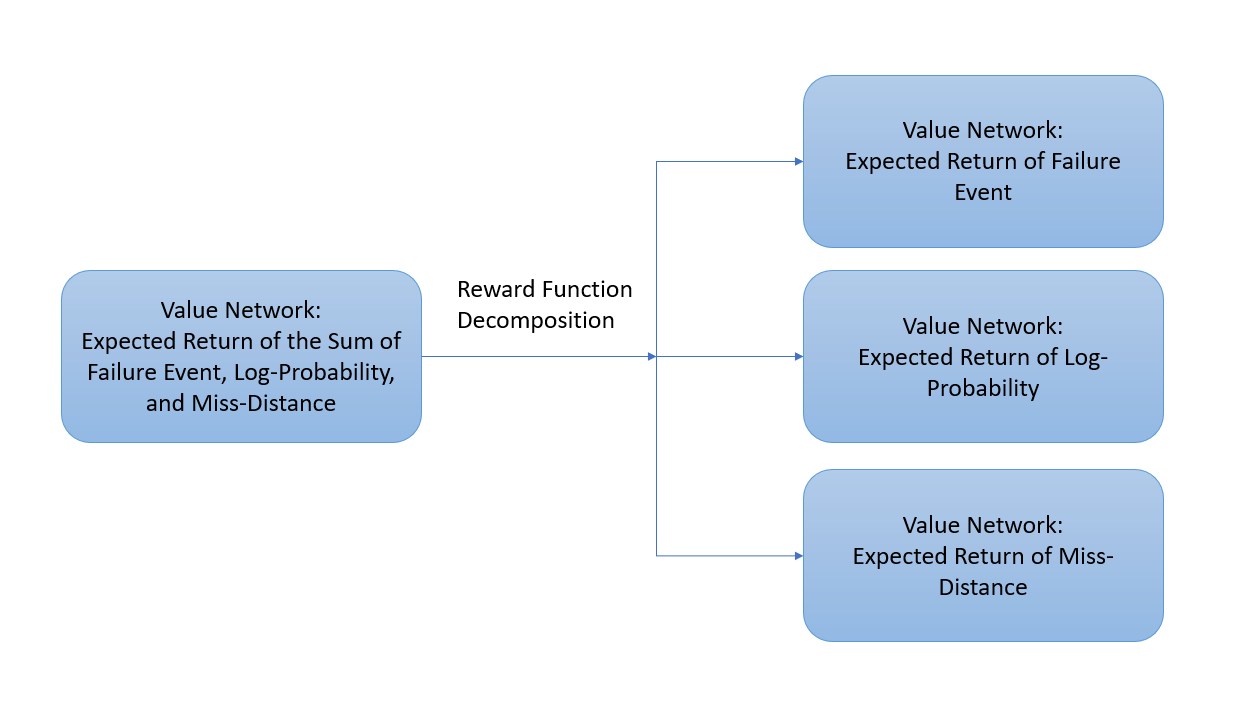
Reward Decomposition for Adaptive Stress Testing

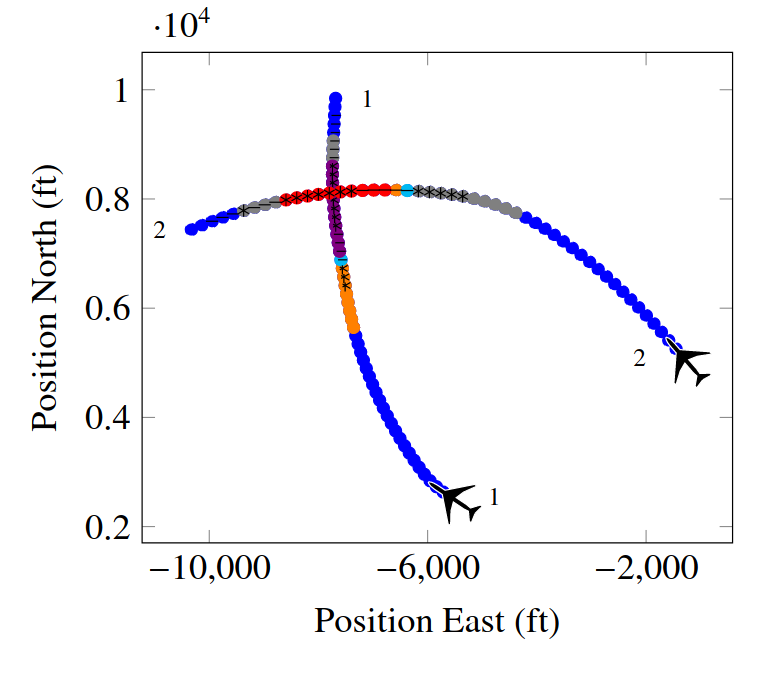


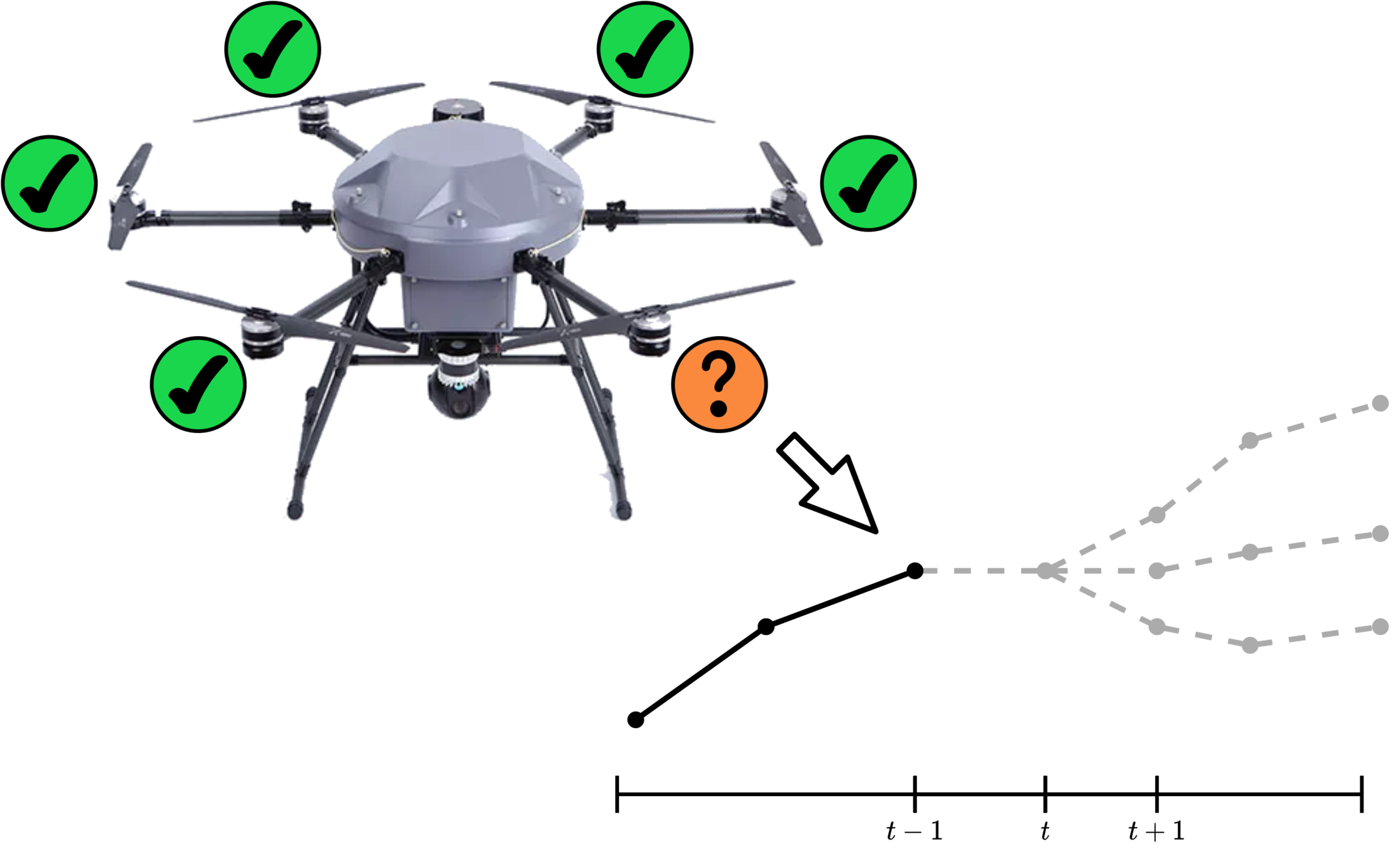
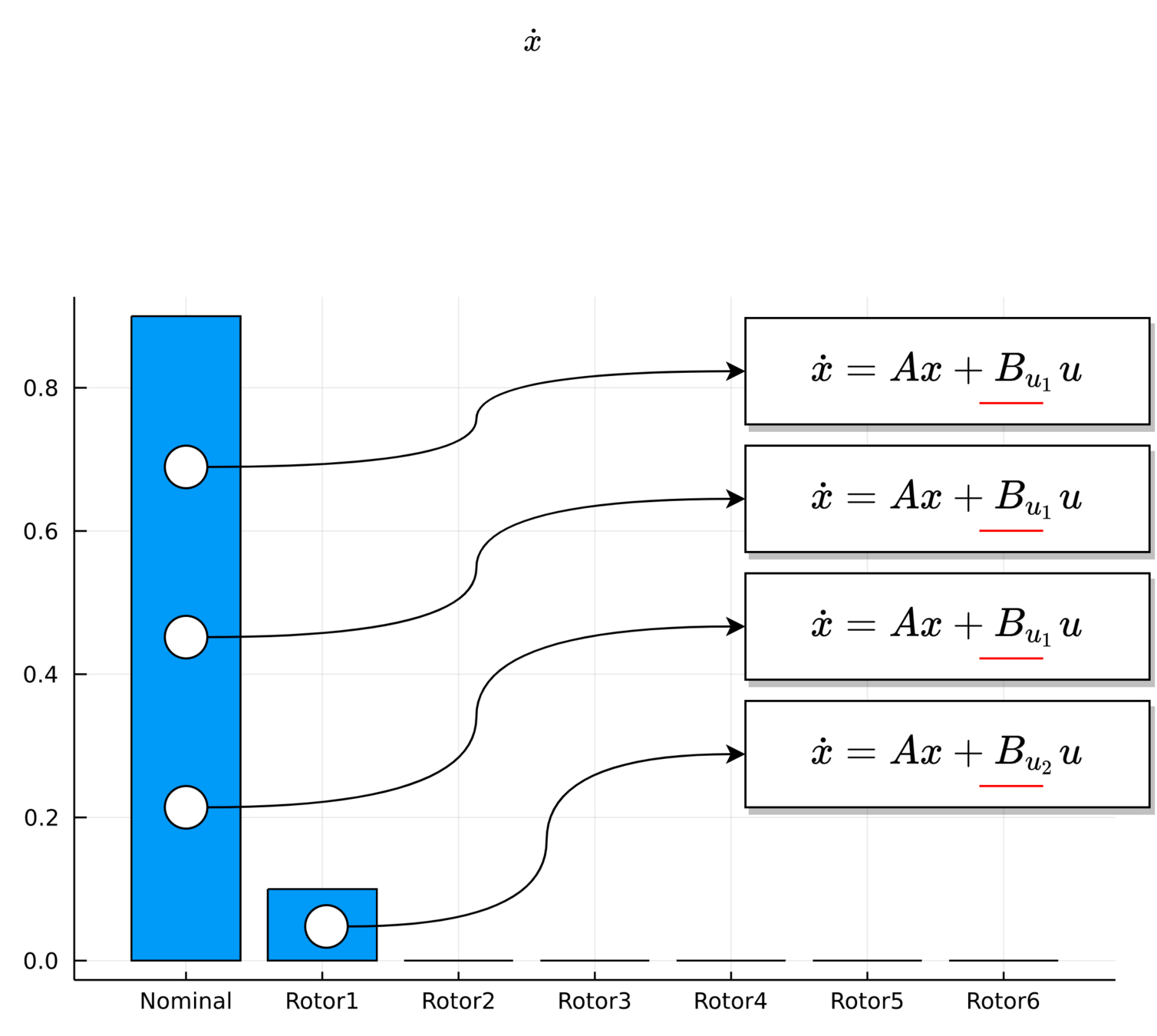
UAV Component Failures
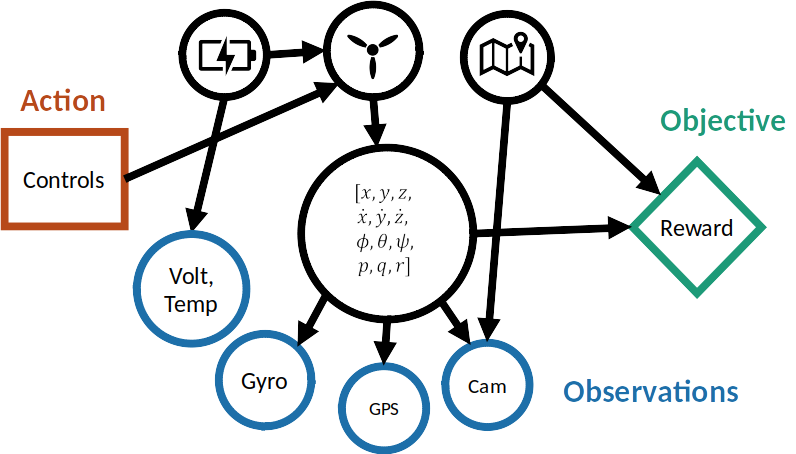
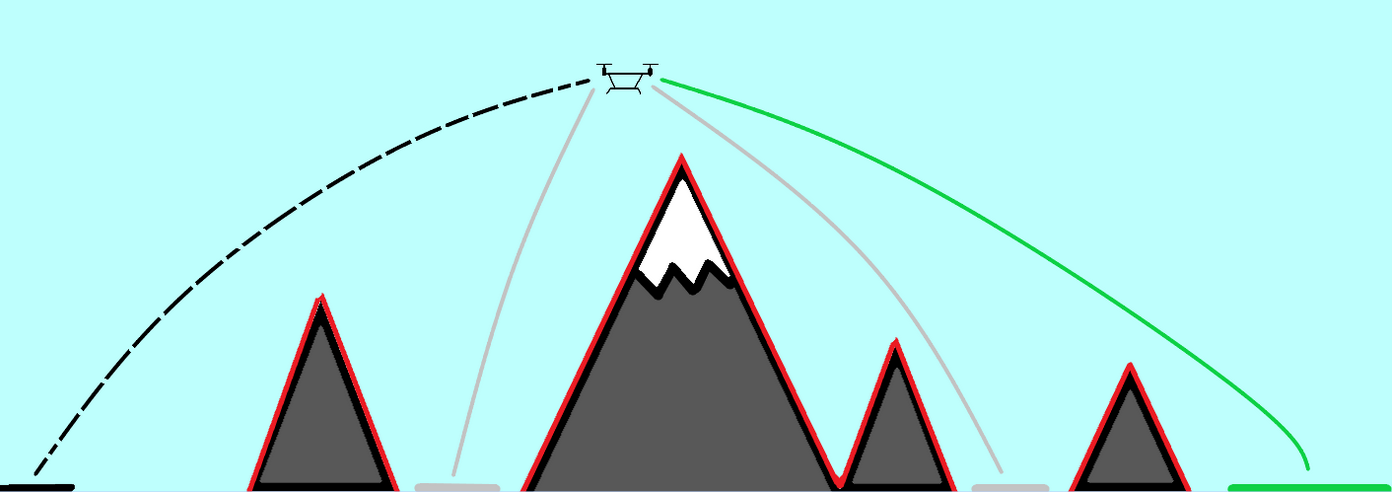

MPC for Intermittent Rotor Failures