Breaking the Curse of Dimensionality in POMDPs with Sampling-based Online Planning

 

Professor Zachary Sunberg

University of Colorado Boulder

Fall 2023

Autonomous Decision and Control Laboratory

cu-adcl.org

  • Algorithmic Contributions
    • Scalable algorithms for partially observable Markov decision processes (POMDPs)
    • Motion planning with safety guarantees
    • Game theoretic algorithms
  • Theoretical Contributions
    • Particle POMDP approximation bounds
  • Applications
    • Space Domain Awareness
    • Autonomous Driving
    • Autonomous Aerial Scientific Missions
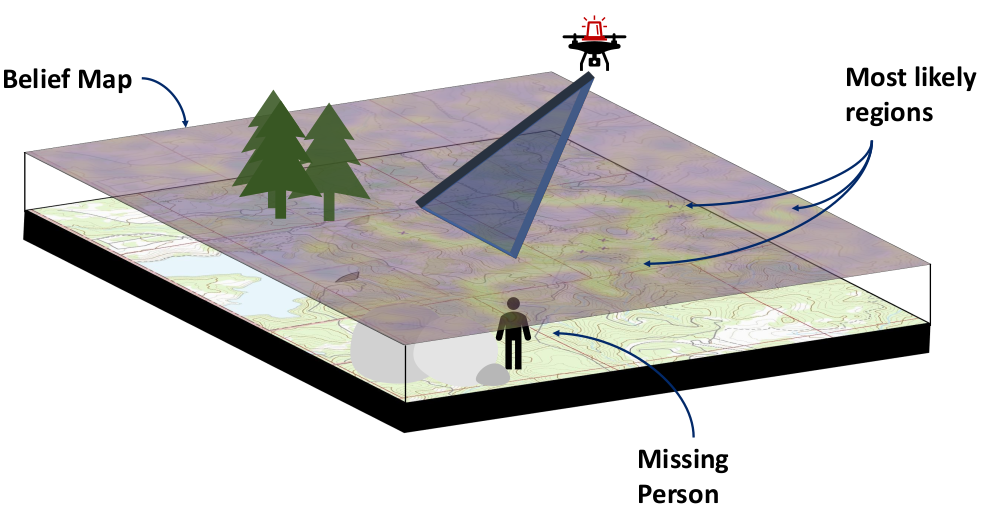
    • Search and Rescue
    • Space Exploration
    • Ecology
  • Open Source Software
    • POMDPs.jl Julia ecosystem

PI: Prof. Zachary Sunberg

PhD Students

Postdoc

The ADCL creates autonomy that is safe and efficient despite uncertainty

Two Objectives for Autonomy

EFFICIENCY

SAFETY

Minimize resource use

(especially time)

Minimize the risk of harm to oneself and others

Safety often opposes Efficiency

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

Outline

  1. The Promise and Curse of POMDPs
  2. Breaking the Curse
  3. Practical Algorithms
  4. Multiple Agents
  5. Open Source Software

Part I: The Promise and Curse of POMDPs

Types of Uncertainty

Alleatory

Epistemic (Static)

Epistemic (Dynamic)

Interaction

MDP

RL

POMDP

Game

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Alleatory

Curse of Dimensionality

\(d\) dimensions, \(k\) segments \(\,\rightarrow \, |S| = k^d\)

1 dimension

e.g. \(s = x \in S = \{1,2,3,4,5\}\)

\(|S| = 5\)

2 dimensions

e.g. \(s = (x,y) \in S = \{1,2,3,4,5\}^2\)

\(|S| = 25\)

3 dimensions

e.g. \(s = (x,y,z) \in S = \{1,2,3,4,5\}^3\)

\(|S| = 125\)

(Discretize each dimension into 5 segments)

Reinforcement Learning

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward

Alleatory

Epistemic (Static)

Partially Observable Markov Decision Process (POMDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}\) - Reward
  • \(\mathcal{O}\) - Observation space
  • \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution

Alleatory

Epistemic (Static)

Epistemic (Dynamic)

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, |s-10|) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

Goal: \(a=0\) at \(s=0\)

Optimal Policy

Localize

\(a=0\)

POMDP Example: Light-Dark

Curse of History in POMDPs

Environment

Policy/Planner

\(a\)

True State

\(s = 7\)

Observation \(o = -0.21\)

Optimal planners need to consider the entire history

\(h_t = (b_0, a_0, o_1, a_1, o_2 \ldots a_{t-1}, o_{t})\)

Bayesian Belief Updates

Environment

Belief Updater

Policy/Planner

\(b\)

\(a\)

\[b_t(s) = P\left(s_t = s \mid b_0, a_0, o_1 \ldots a_{t-1}, o_{t}\right)\]

True State

\(s = 7\)

Observation \(o = -0.21\)

\(O(|S|^2)\)

\[ = P\left(s_t = s \mid b_{t-1}, a_{t-1}, o_{t}\right)\]

A POMDP is an MDP on the Belief Space

POMDP \((S, A, T, R, O, Z)\) is equivalent to MDP \((S', A', T', R')\)

  • \(S' = \Delta(S)\)
  • \(A' = A\)
  • \(T'\) defined by belief updates (\(T\) and \(Z\))
  • \(R'(b, a) = \underset{s \sim b}{E}[R(s, a)]\)

One new continuous state dimension for each state in \(S\)!

POMDP (decision problem) is PSPACE Complete

Part II: Breaking the Curse

Integration

Find \(\underset{s\sim b}{E}[f(s)]\)

\[=\sum_{s \in S} f(s) b(s)\]

Monte Carlo Integration

\(Q_N \equiv \frac{1}{N} \sum_{i=1}^N f(s_i)\)

\(s_i \sim b\)     i.i.d.

\(\text{Var}(Q_N) = \text{Var}\left(\frac{1}{N} \sum_{i=1}^N f(s_i)\right)\)

\(= \frac{1}{N^2} \sum_{i=1}^N\text{Var}\left(f(s_i)\right)\)

\(= \frac{1}{N} \text{Var}\left(f(s_i)\right)\)

\[P(|Q_N - E[f(s_i)]| \geq \epsilon) \leq \frac{\text{Var}(f(s_i))}{N \epsilon^2}\]

(Bienayme)

(Chebyshev)

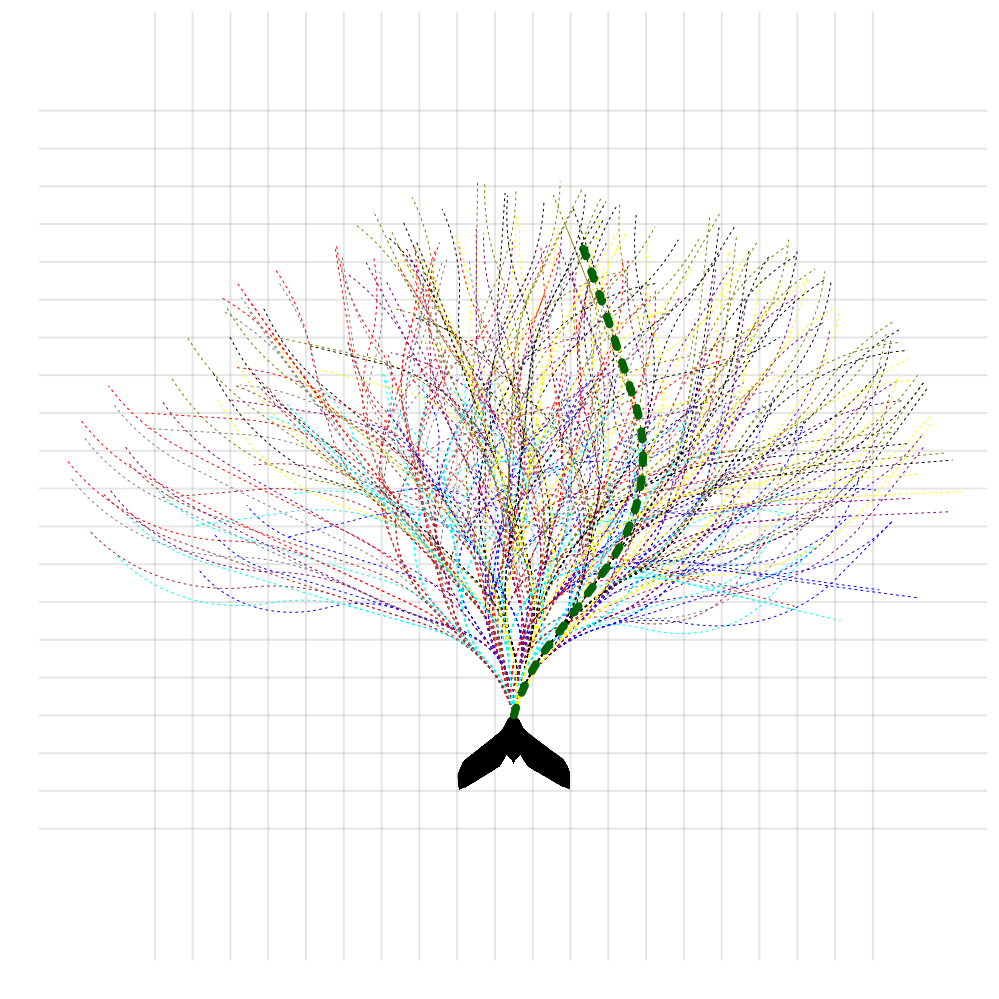
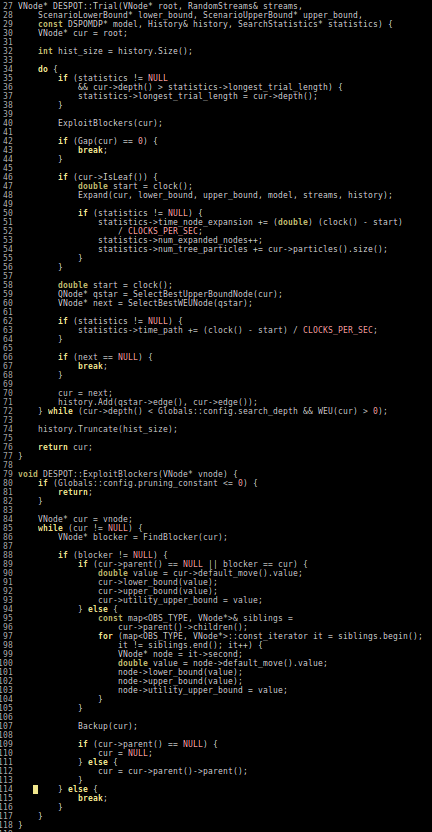
Online Tree Search in MDPs

Time

Estimate \(Q(s, a)\) based on children

Sparse Sampling

Expand for all actions (\(\left|\mathcal{A}\right| = 2\) in this case)

...

Expand for all \(\left|\mathcal{S}\right|\) states

\(C=3\) states

Just apply to History MDP?

No! You can't simulate the next history based on the previous history

Just apply to Belief MDP?

No! Exact belief updates \(O(|S|^2)\)

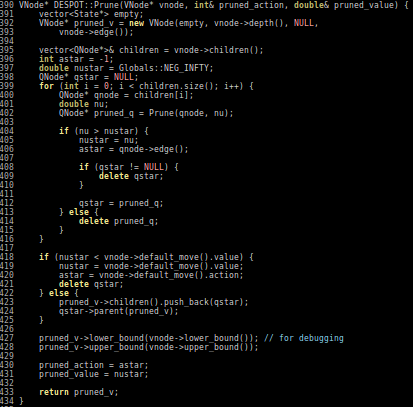
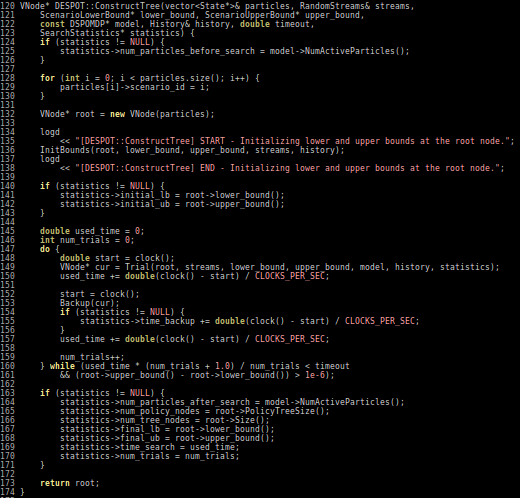
Particle Filter POMDP Approximation

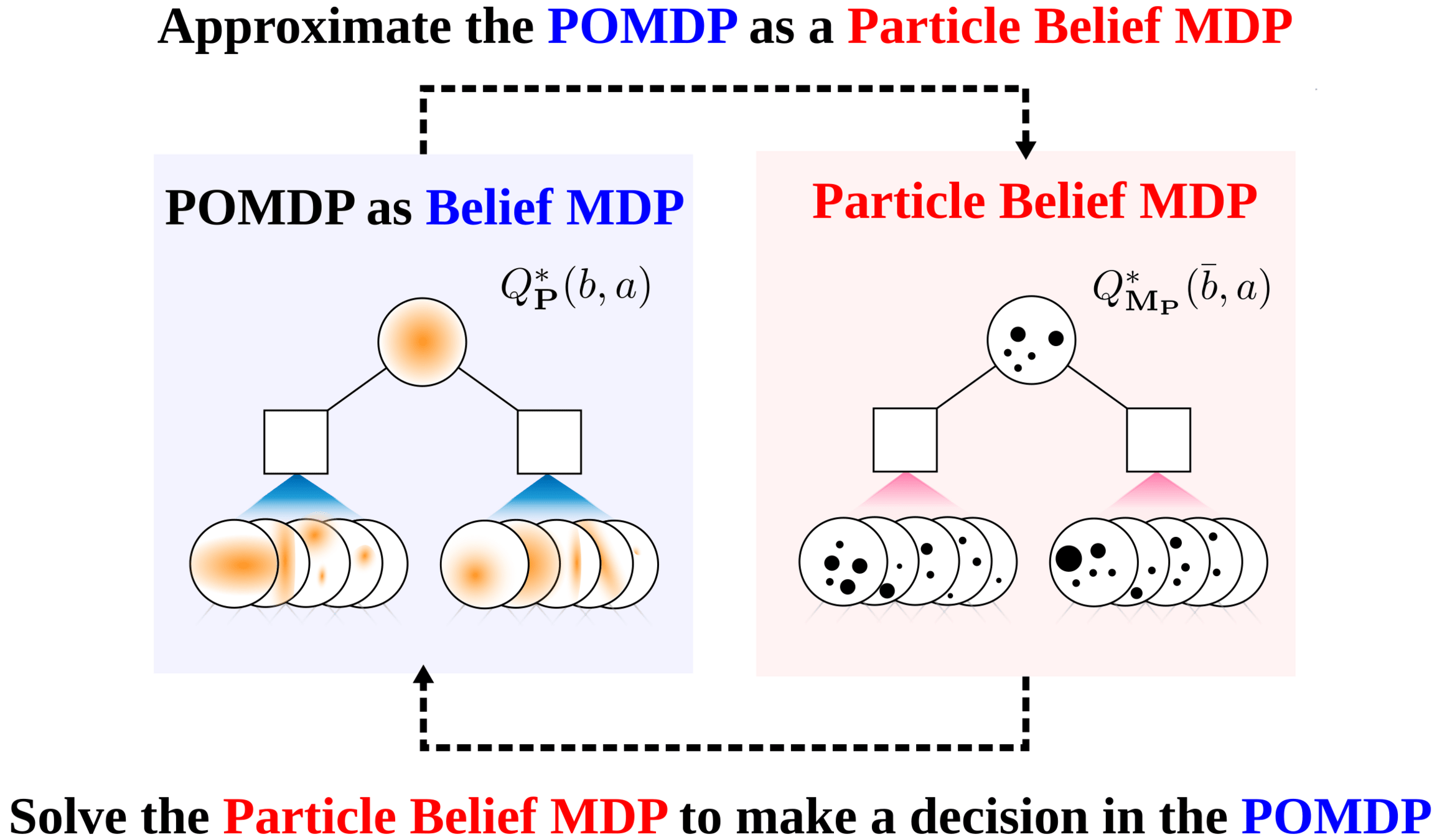
\[b(s) \approx \sum_{i=1}^N \delta_{s}(s_i)\; w_i\]

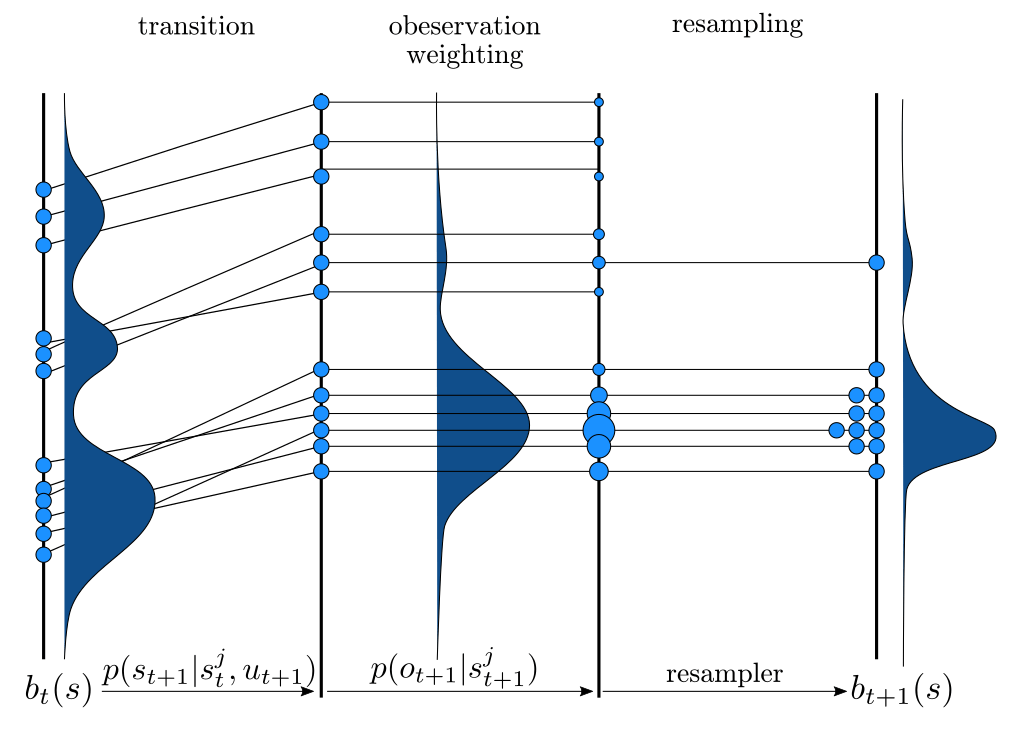
POMDP Assumptions for Proofs

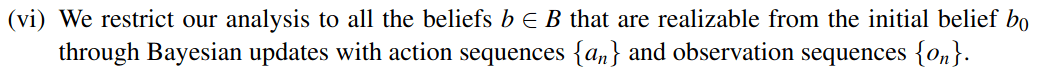
Continuous \(S\), \(O\); Discrete \(A\)

No Dirac-delta observation densities

Bounded Reward

Generative model for \(T\); Explicit model for \(Z\)

Finite Horizon

Only reasonable beliefs

Self Normalized Infinite Renyi Divergence Concentation

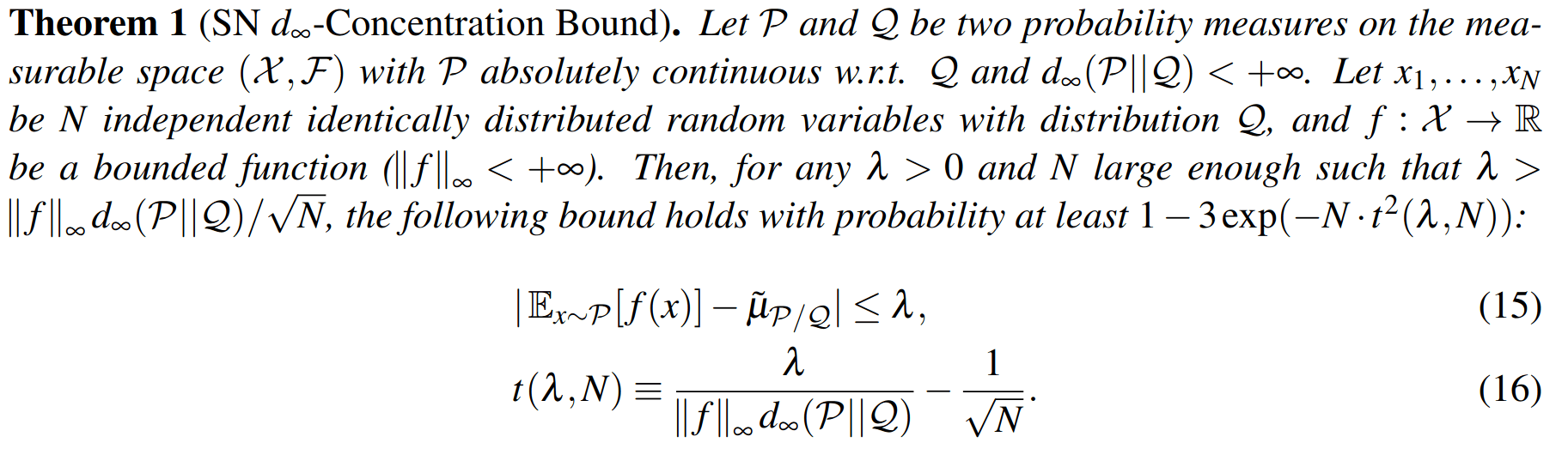
Sparse Sampling-\(\omega\)

SS-\(\omega\) close to Particle Belief MDP (in terms of Q)

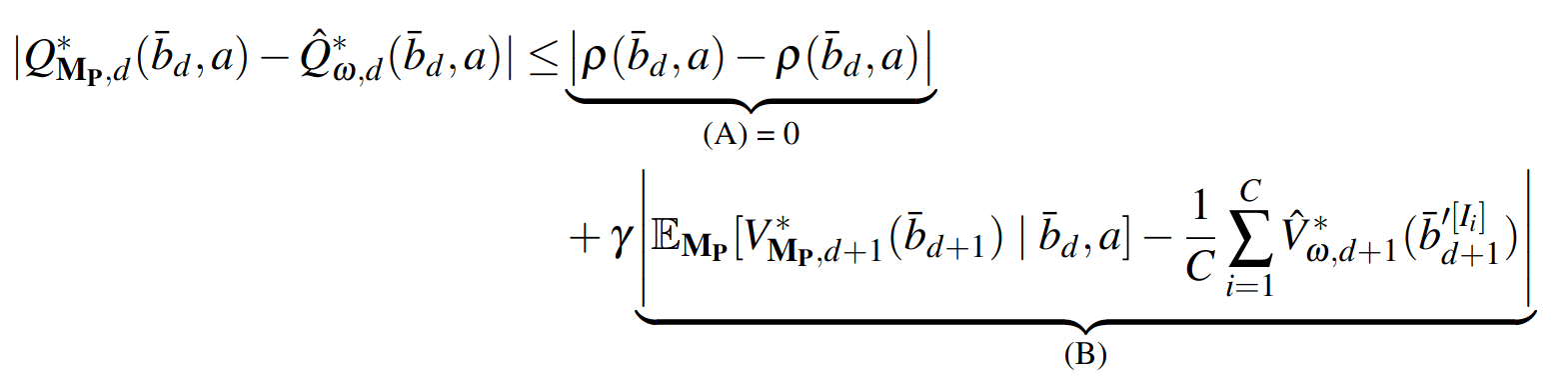
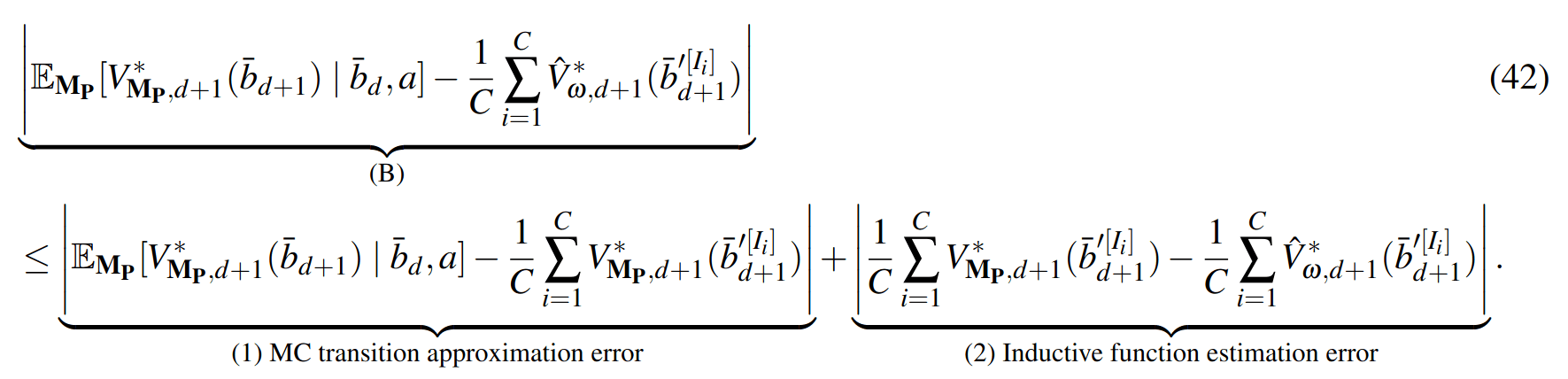
SS-\(\omega\) is close to Belief MDP

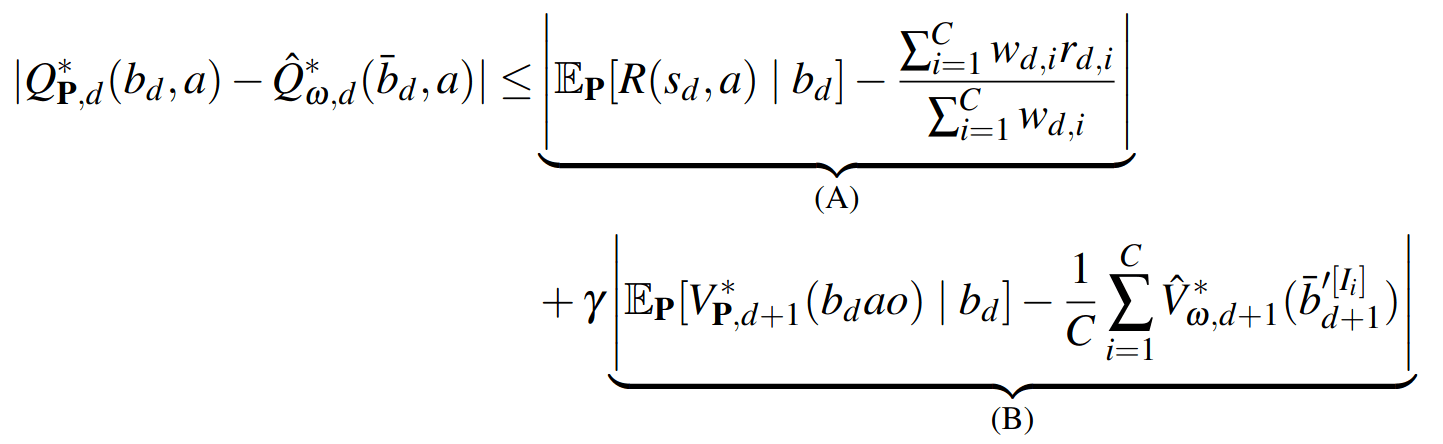
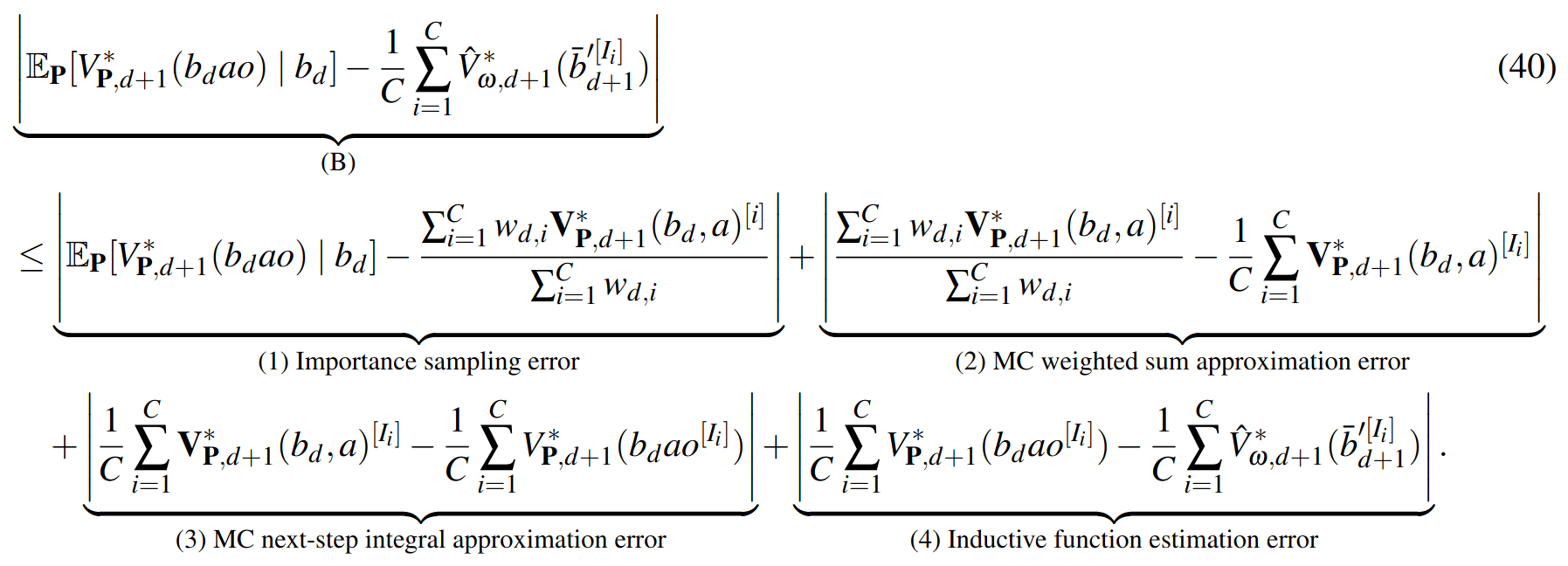
PF Approximation Accuracy

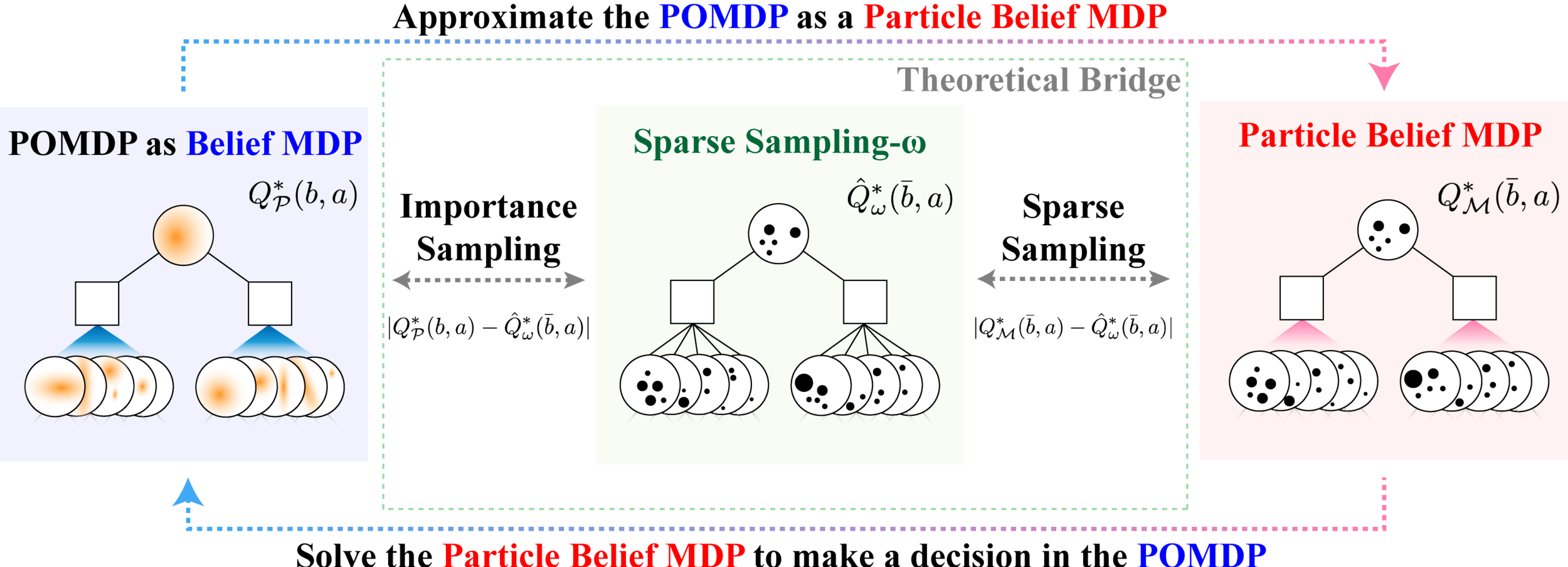
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]

For any \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,

[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, JAIR 2023]

No dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!

Particle belief planning suboptimality

\(C\) is too large for any direct safety guarantees. But, in practice, works extremely well for improving efficiency.

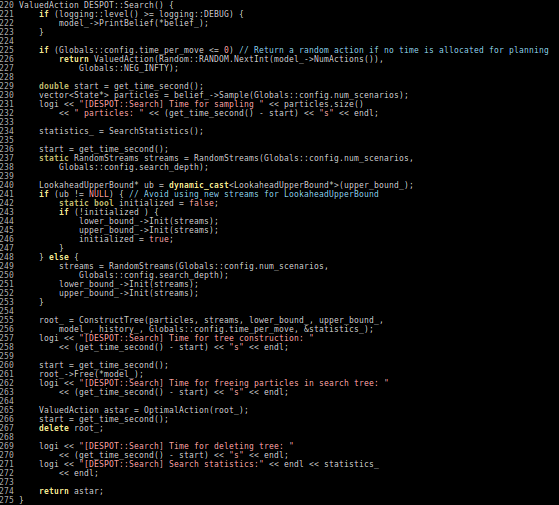
Part III: Practical Algorithms

Easy MDP to POMDP Extension

POMCPOW: Gradually adds particles to beliefs (Empirically more efficient, but no known guarantees)

POMDP Formulation

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)

Ego external state

External states of other cars

Internal states of other cars

External states of other cars

  • Actions shielded (based only on external states) so they can never cause crashes
  • Braking action always available

Efficiency

Safety

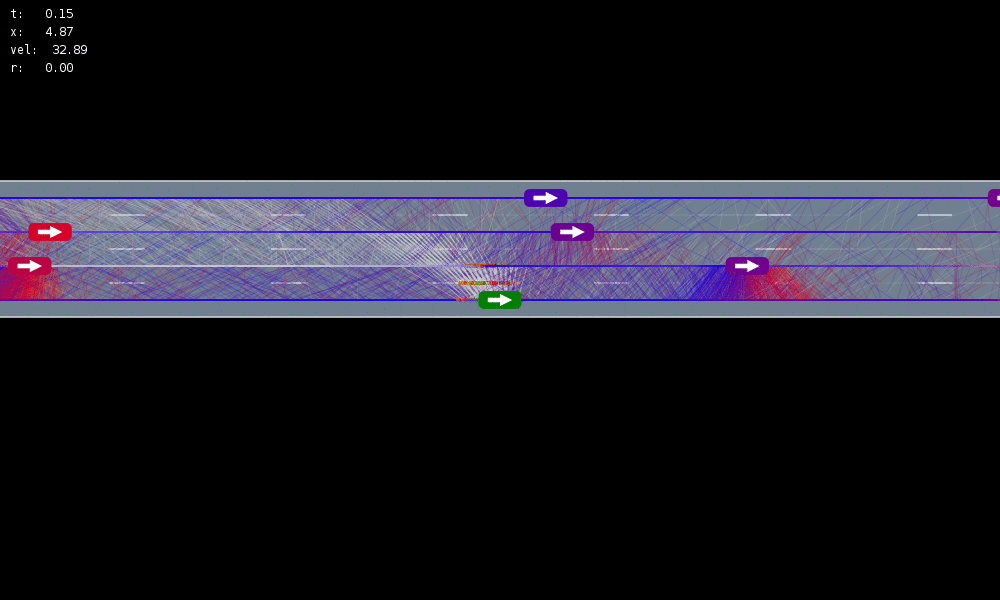
MDP trained on normal drivers

MDP trained on all drivers

Omniscient

POMCPOW (Ours)

Simulation results

[Sunberg & Kochenderfer, T-ITS 2023]

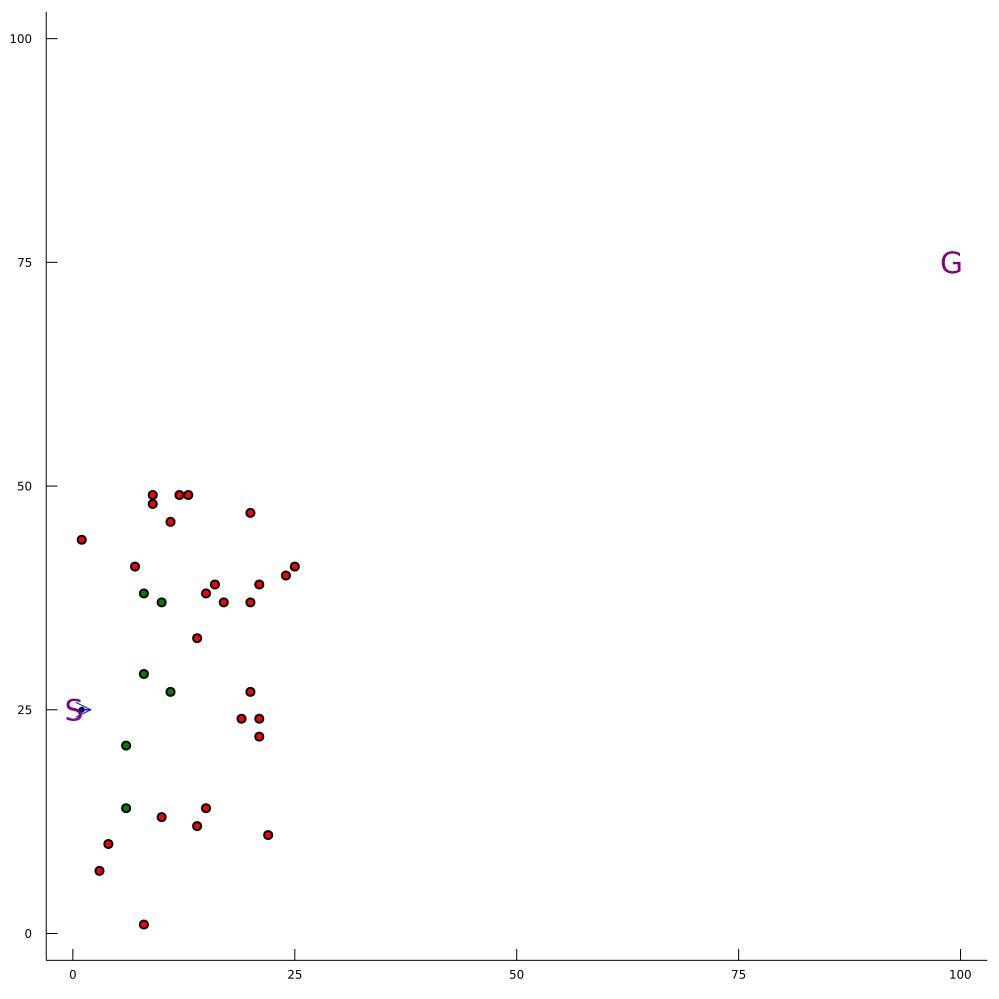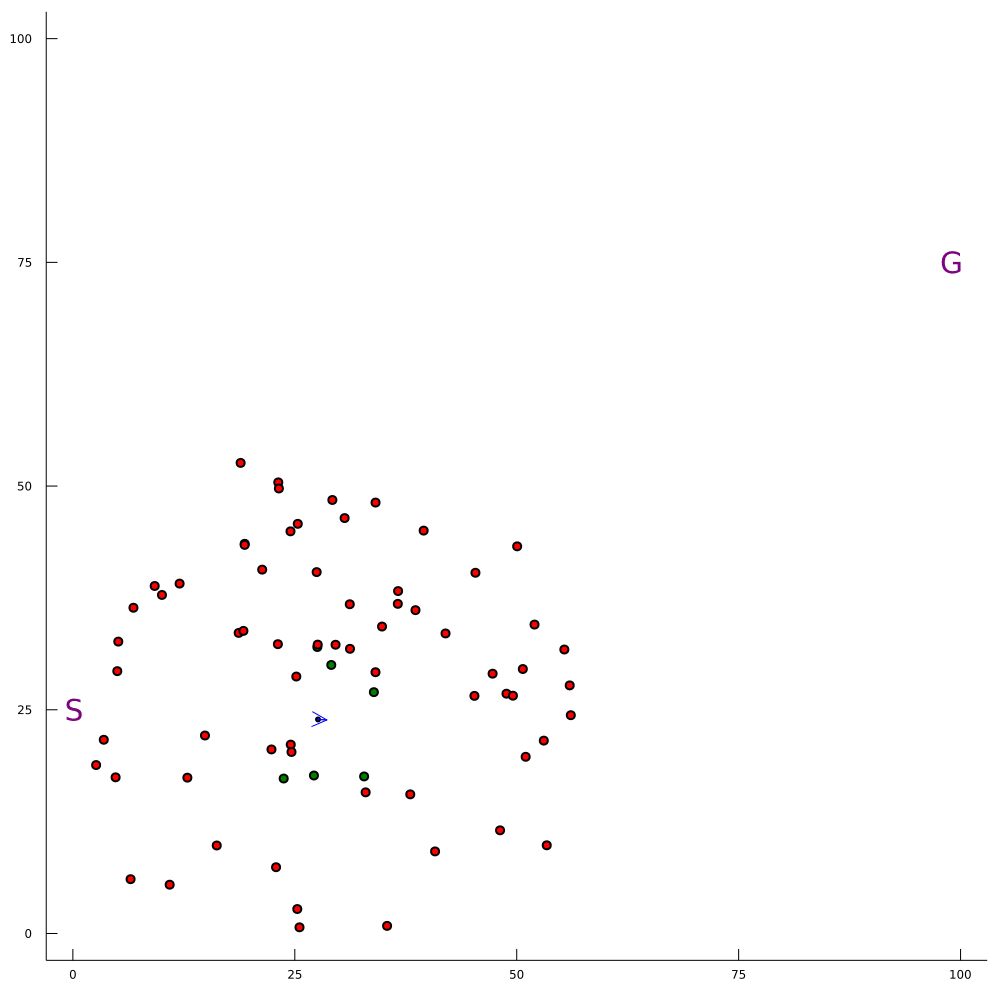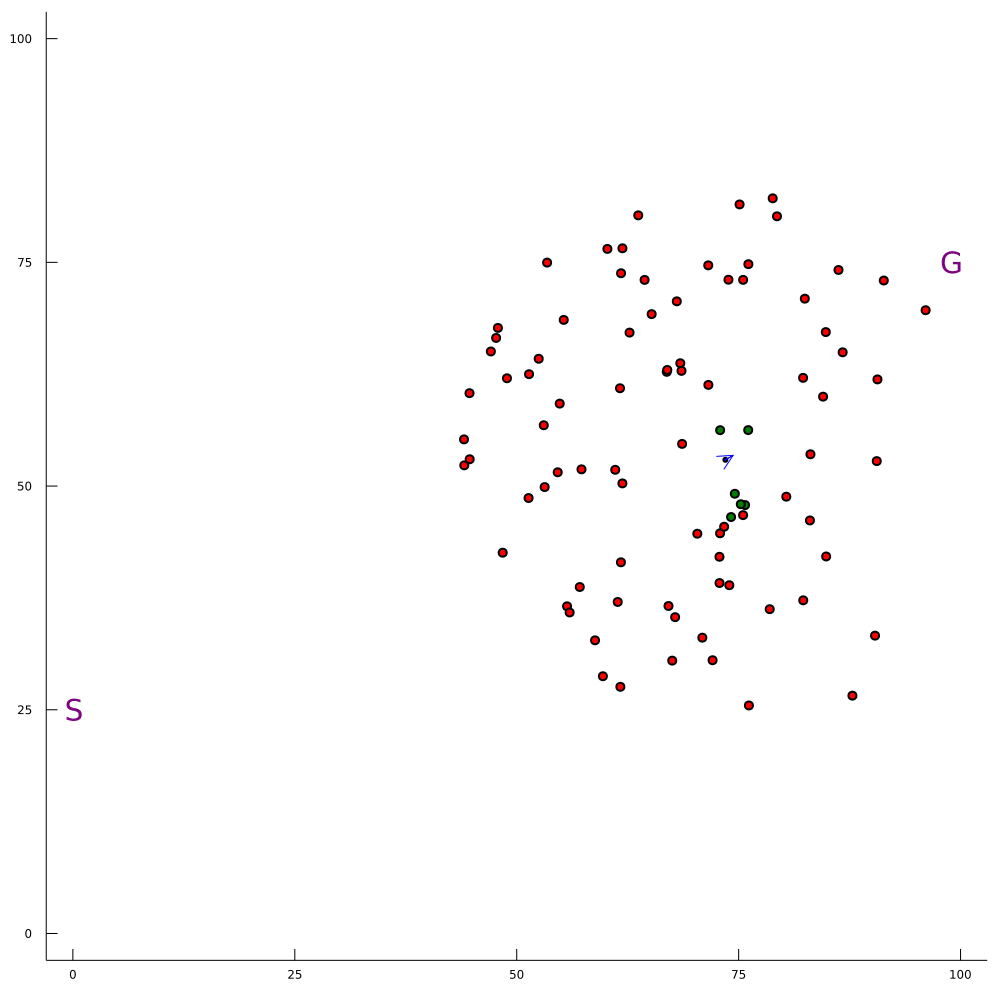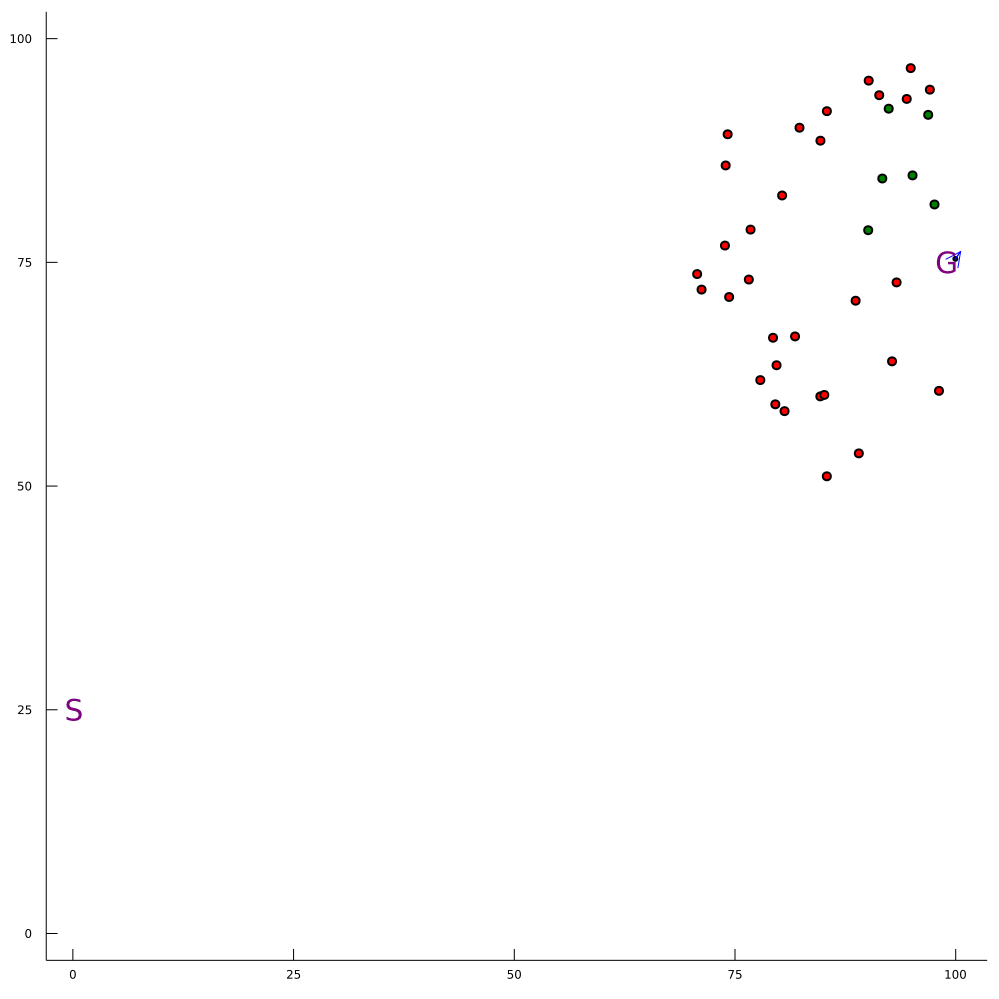
Conventional 1DOF POMDP

Multi-DOF POMDP

Pedestrian Navigation

[Gupta, Hayes, & Sunberg, AAMAS 2021]

Storm Science

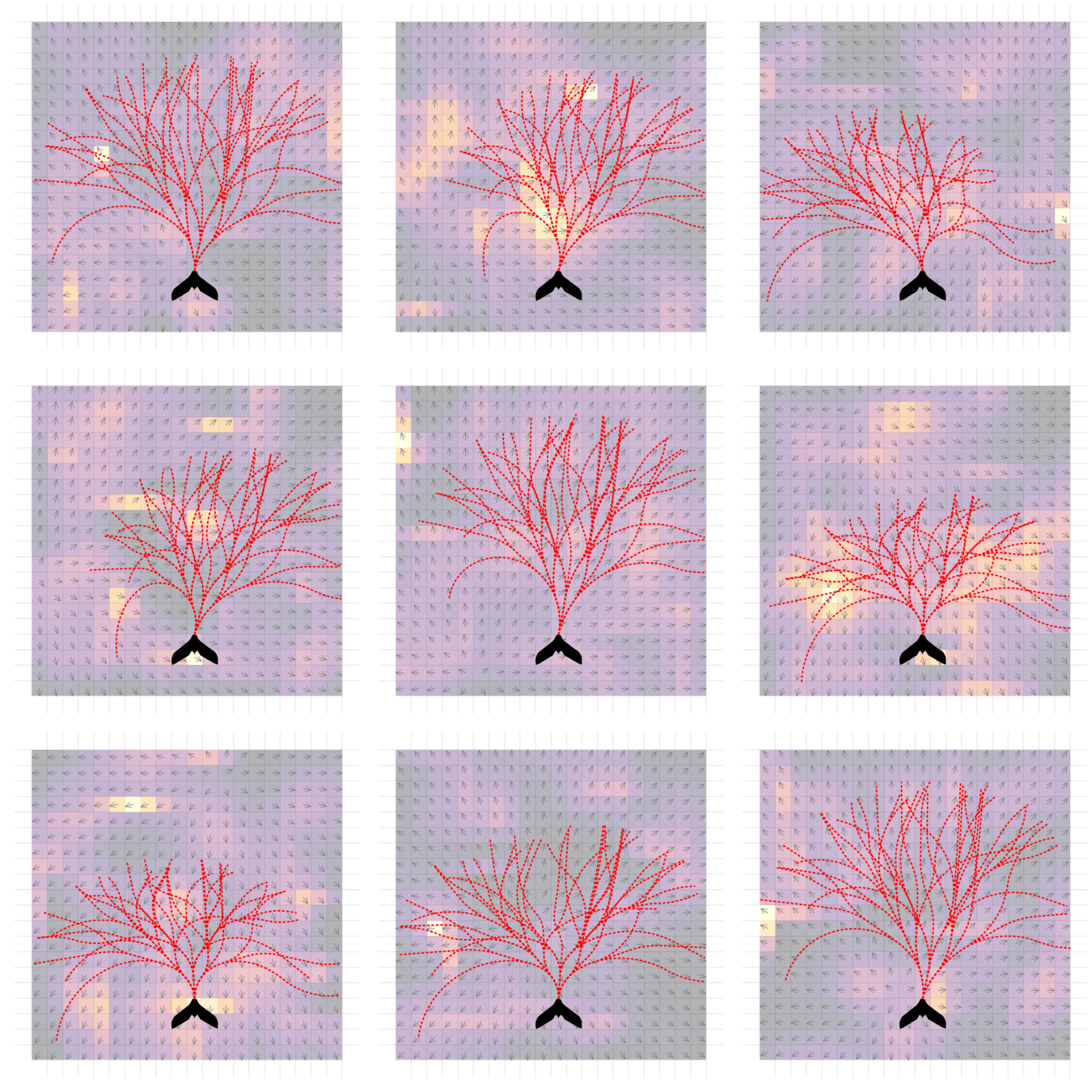
POMDP Planning with Learned Components

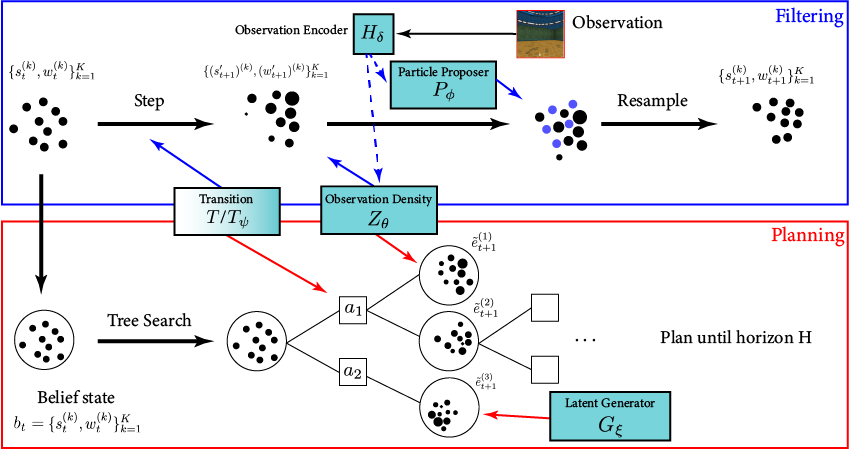
[Deglurkar, Lim, Sunberg, & Tomlin, 2023]

Continuous \(A\): BOMCP

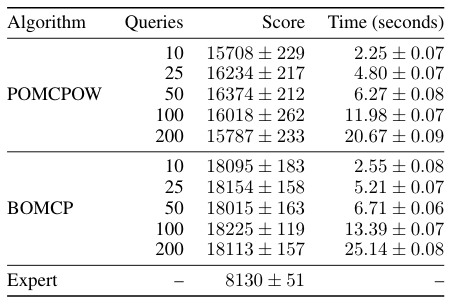
[Mern, Sunberg, et al. AAAI 2021]

Continuous \(A\): Voronoi Progressive Widening

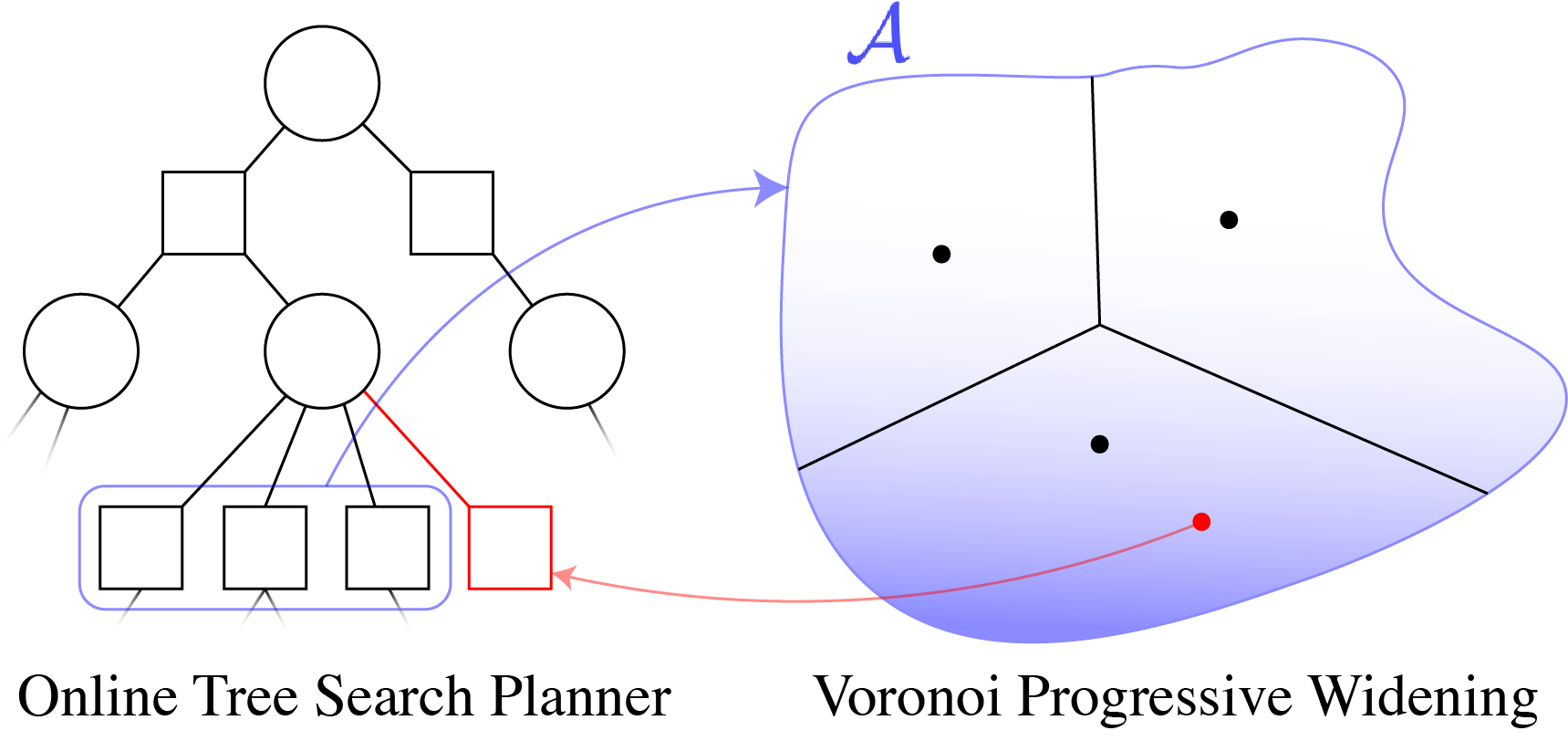
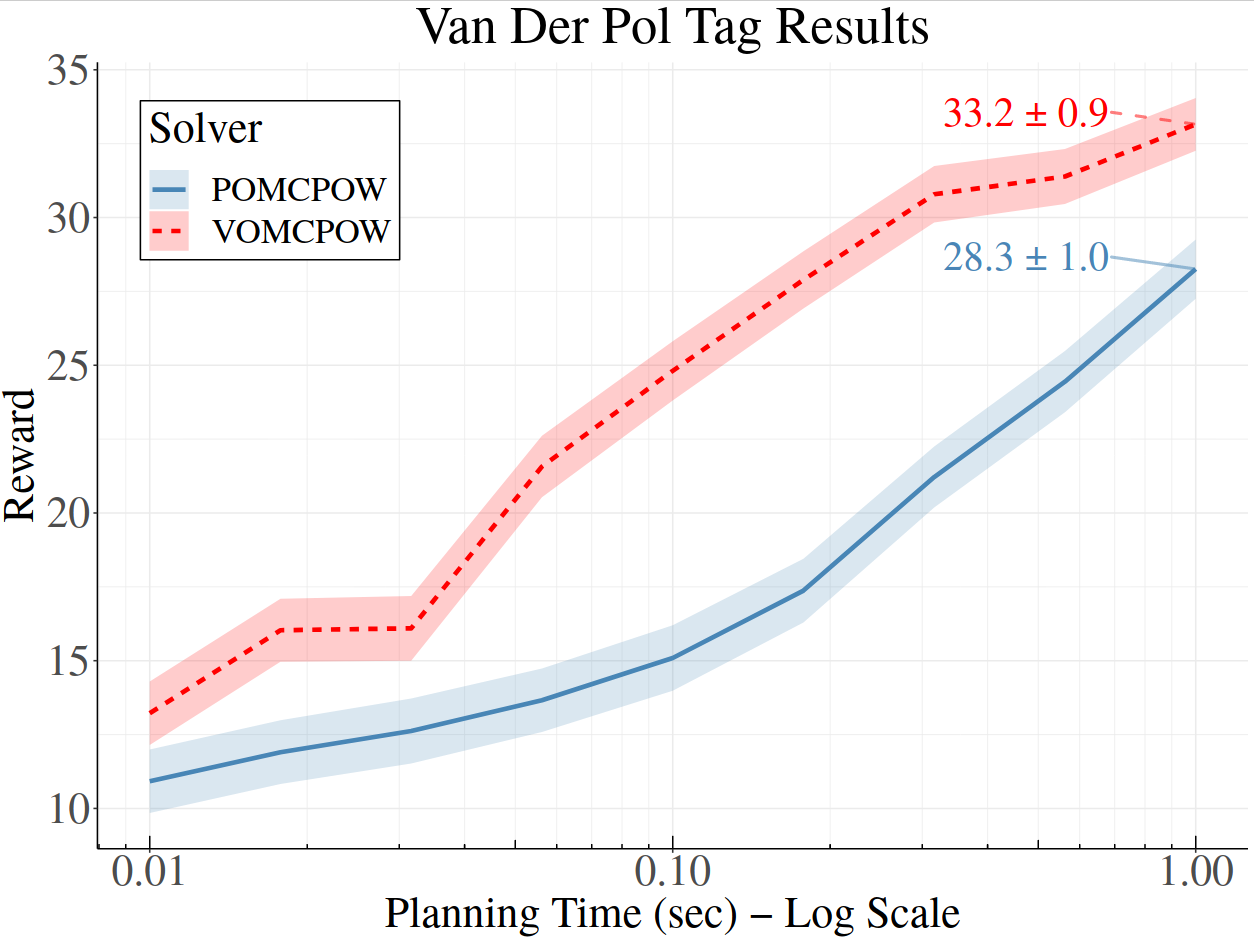
[Lim, Tomlin, & Sunberg CDC 2021]

Explainability

Provide explanations to improve trust and enable cooperation

"Action 2 accounts for changes in availability window"

Explanation

i

1

2

1

2

Part IV: Multiple Agents

Partially Observable Markov Game

Alleatory

Epistemic (Static)

Epistemic (Dynamic)

Interaction

  • \(\mathcal{S}\) - State space
  • \(T(s' \mid s, \bm{a})\) - Transition probability distribution
  • \(\mathcal{A}^i, \, i \in 1..k\) - Action spaces
  • \(R^i(s, \bm{a})\) - Reward function
  • \(\mathcal{O}^i, \, i \in 1..k\) - Observation space
  • \(Z(o^i \mid \bm{a}, s')\) - Observation probability distribution

Game Theory

Nash Equilibrium: All players play a best response.

Optimization Problem

(MDP or POMDP)

\(\text{maximize} \quad f(x)\)

Game

Player 1: \(U_1 (a_1, a_2)\)

Player 2: \(U_2 (a_1, a_2)\)

Collision

Example: Airborne Collision Avoidance


 

 

Player 1

Player 2

Up

Down

Up

Down

-6, -6

-1, 1

1, -1

-4, -4

Collision

Mixed Strategies

Nash Equilibrium \(\iff\) Zero Exploitability

\[\sum_i \max_{\pi_i'} U_i(\pi_i', \pi_{-i})\]

No Pure Nash Equilibrium!

Instead, there is a Mixed Nash where each player plays up or down with 50% probability.

If either player plays up or down more than 50% of the time, their strategy can be exploited.

Exploitability (zero sum):

Strategy (\(\pi_i\)): probability distribution over actions


 

 

Up

Down

Up

Down

-1, 1

1, -1

1, -1

-1, 1

Collision

Collision

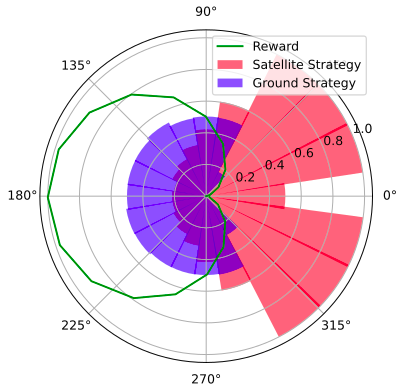
Space Domain Awareness Games

Simplified SDA Game

1

2

...

...

...

...

...

...

...

\(N\)

[Becker & Sunberg CDC 2021]

Counterfactual Regret Minimization Training

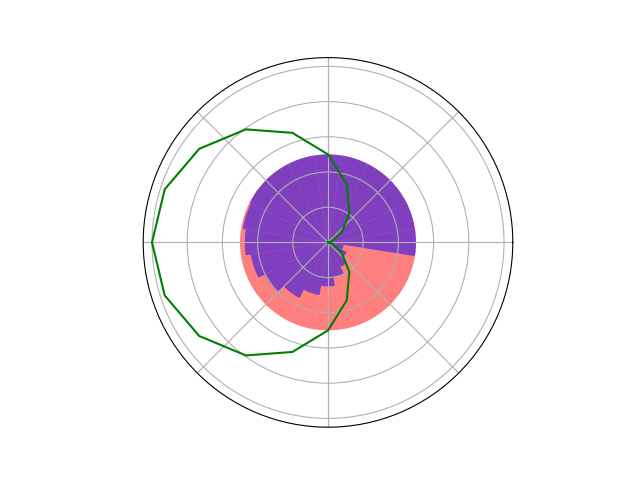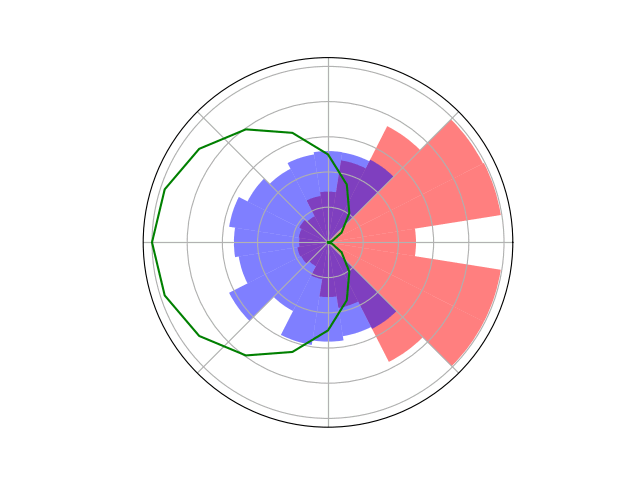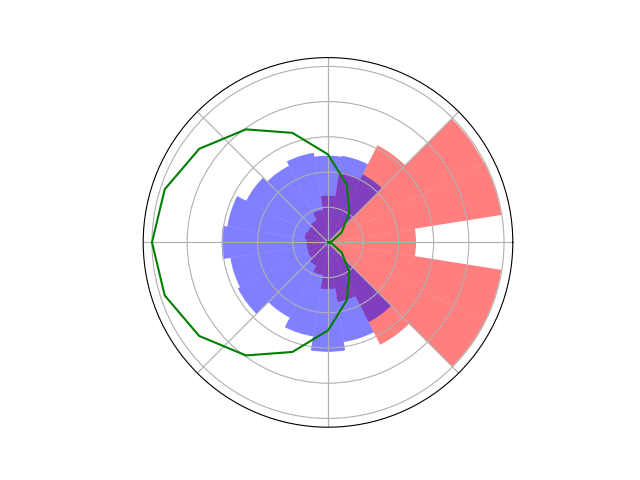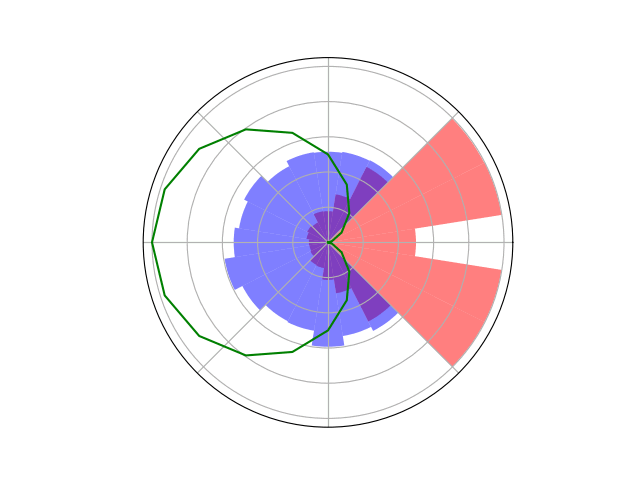
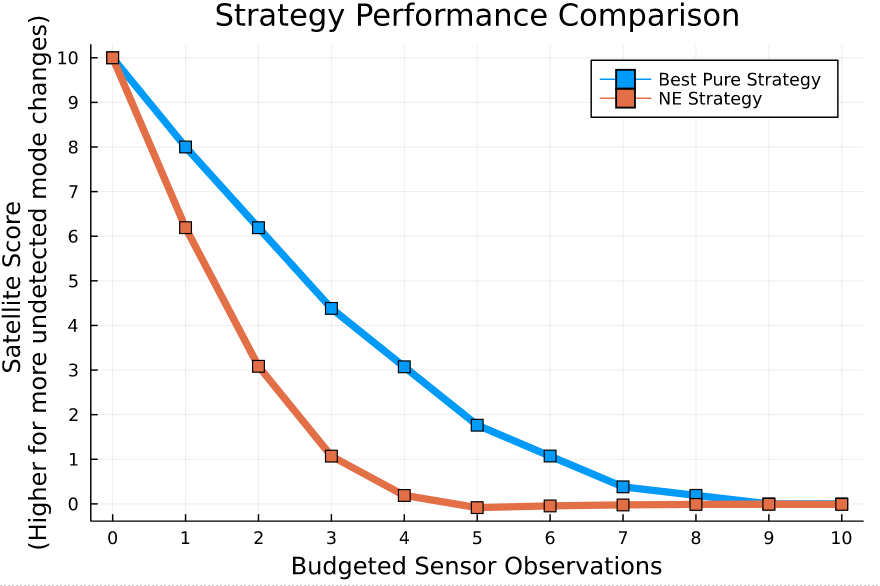
Open question: are there \(\mathcal{S}\)- and \(\mathcal{O}\)-independent algorithms for POMGs?

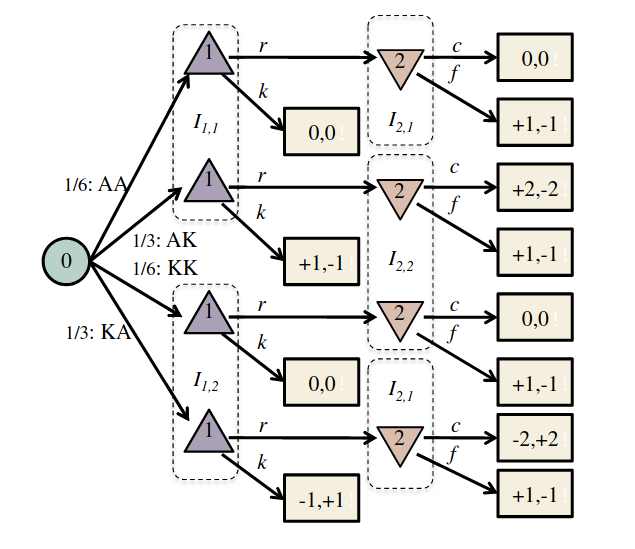
Incomplete Information Extensive form Game

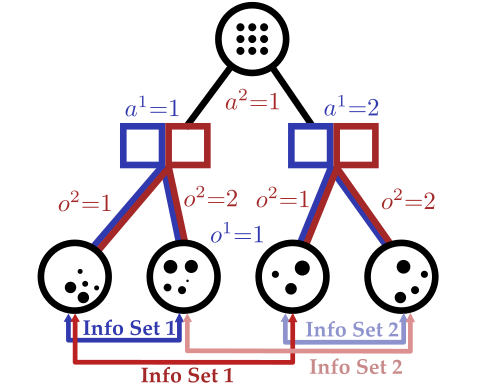
Our new algorithm for POMGs

Part V: Open Source Research Software

Good Examples

  • Open AI Gym interface
  • OMPL
  • ROS

Challenges for POMDP Software

  1. There is a huge variety of
    • Problems
      • Continuous/Discrete
      • Fully/Partially Observable
      • Generative/Explicit
      • Simple/Complex
    • Solvers
      • Online/Offline
      • Alpha Vector/Graph/Tree
      • Exact/Approximate
    • Domain-specific heuristics
  2. POMDPs are computationally difficult.

Explicit

Black Box

("Generative" in POMDP lit.)

\(s,a\)

\(s', o, r\)

Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

Open Source Research Software

  • Performant
  • Flexible and Composable
  • Free and Open
  • Easy for a wide range of people to use (for homework)
  • Easy for a wide range of people to understand

C++

Python, C++

Python, Matlab

Python, Matlab

Python, C++

2013

We love [Matlab, Lisp, Python, Ruby, Perl, Mathematica, and C]; they are wonderful and powerful. For the work we do — scientific computing, machine learning, data mining, large-scale linear algebra, distributed and parallel computing — each one is perfect for some aspects of the work and terrible for others. Each one is a trade-off.

We are greedy: we want more.

2012

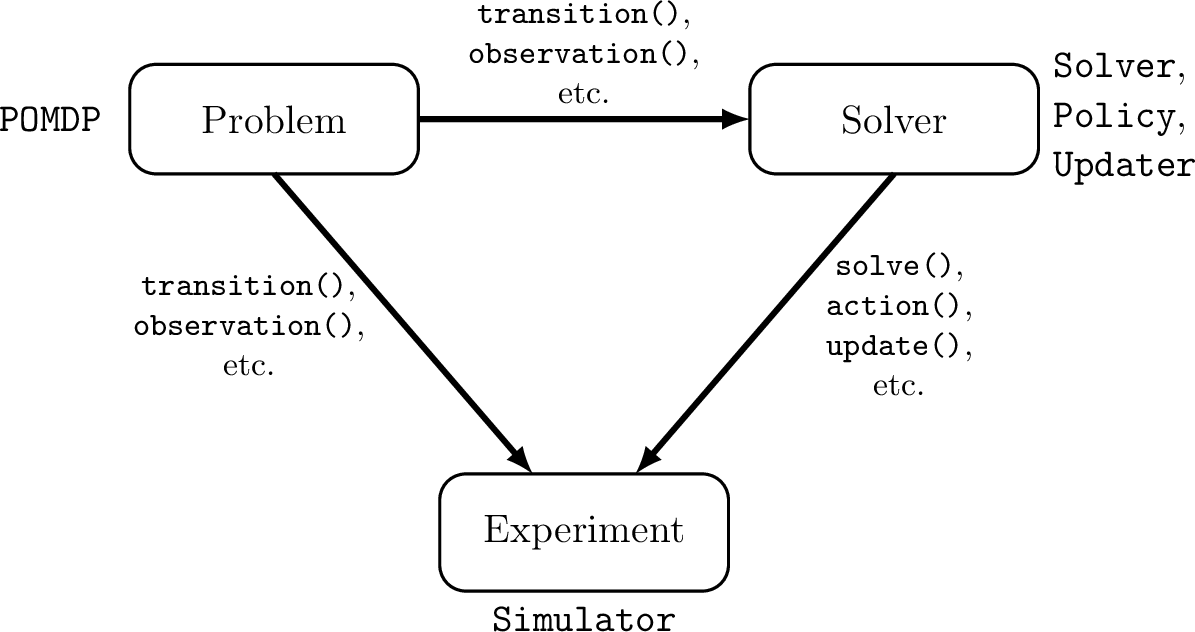
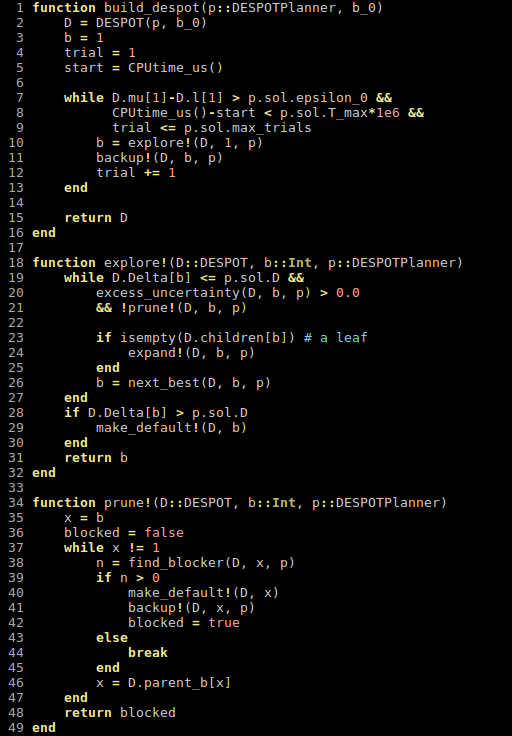
POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

Mountain Car

partially_observable_mountaincar = QuickPOMDP(
    actions = [-1., 0., 1.],
    obstype = Float64,
    discount = 0.95,
    initialstate = ImplicitDistribution(rng -> (-0.2*rand(rng), 0.0)),
    isterminal = s -> s[1] > 0.5,

    gen = function (s, a, rng)        
        x, v = s
        vp = clamp(v + a*0.001 + cos(3*x)*-0.0025, -0.07, 0.07)
        xp = x + vp
        if xp > 0.5
            r = 100.0
        else
            r = -1.0
        end
        return (sp=(xp, vp), r=r)
    end,

    observation = (a, sp) -> Normal(sp[1], 0.15)
)
using POMDPs
using QuickPOMDPs
using POMDPPolicies
using Compose
import Cairo
using POMDPGifs
import POMDPModelTools: Deterministic

mountaincar = QuickMDP(
    function (s, a, rng)        
        x, v = s
        vp = clamp(v + a*0.001 + cos(3*x)*-0.0025, -0.07, 0.07)
        xp = x + vp
        if xp > 0.5
            r = 100.0
        else
            r = -1.0
        end
        return (sp=(xp, vp), r=r)
    end,
    actions = [-1., 0., 1.],
    initialstate = Deterministic((-0.5, 0.0)),
    discount = 0.95,
    isterminal = s -> s[1] > 0.5,

    render = function (step)
        cx = step.s[1]
        cy = 0.45*sin(3*cx)+0.5
        car = (context(), circle(cx, cy+0.035, 0.035), fill("blue"))
        track = (context(), line([(x, 0.45*sin(3*x)+0.5) for x in -1.2:0.01:0.6]), stroke("black"))
        goal = (context(), star(0.5, 1.0, -0.035, 5), fill("gold"), stroke("black"))
        bg = (context(), rectangle(), fill("white"))
        ctx = context(0.7, 0.05, 0.6, 0.9, mirror=Mirror(0, 0, 0.5))
        return compose(context(), (ctx, car, track, goal), bg)
    end
)

energize = FunctionPolicy(s->s[2] < 0.0 ? -1.0 : 1.0)
makegif(mountaincar, energize; filename="out.gif", fps=20)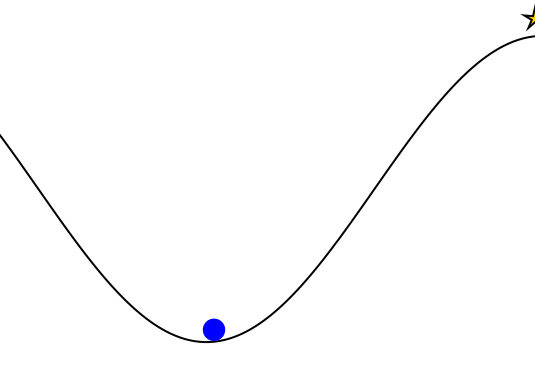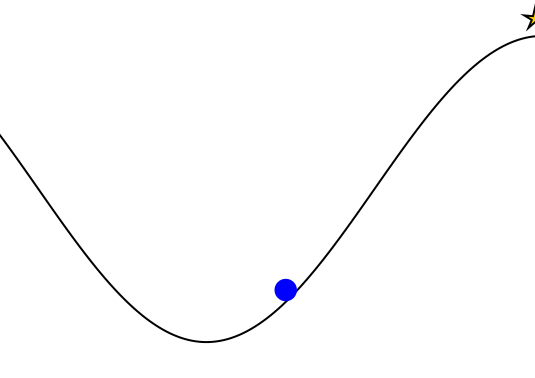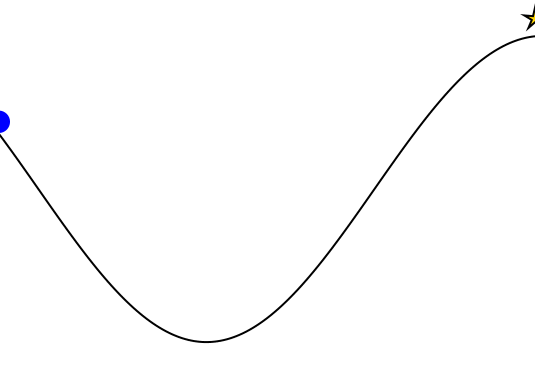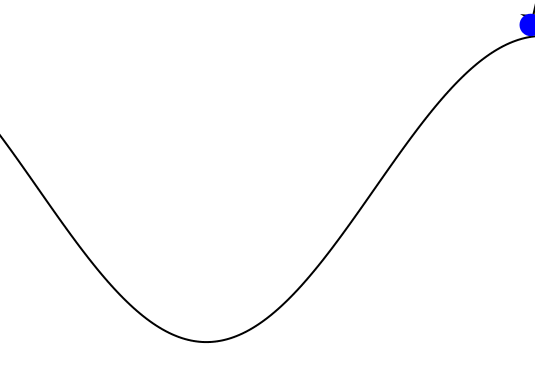

Thank You!

www.cu-adcl.org

This work was led by Michael Lim, Himanshu Gupta, Tyler Becker, Sampada Deglurkar, John Mern, with assistance from others (https://www.cu-adcl.org/people/)

Recent and Current Projects

Human Behavior Model: IDM and MOBIL

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).

A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).

A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).

All drivers normal

Omniscient

Mean MPC

QMDP

POMCPOW