Bayesian Networks
Today:
- Bayesian Networks
- How do we reason about independence in Bayesian Networks?
- How do we sample from Bayesian Networks?
Next Year: emphasize yes/inconclusive d-separation outcome
2022 Quiz 1

Review of Definitions
Bayesian Network: Directed Acyclic Graph (DAG) that represents a joint probability distribution
- Node:
- Edges encode:
Random Variable
Independence
\(P(X, Y) = P(X)\, P(Y)\)
Conditional Independence
\(P(X, Y \mid Z) = P(X \mid Z) \, P(Y \mid Z)\)
\[P(x_{1:n}) = \prod_{i=1}^n P(x_i \mid \text{pa}(x_i))\]
What does conditional independence mean?
All of \(X\)'s dependence on \(Y\) comes through \(Z\)
\(X \perp Y \mid Z\)
\(\implies\)
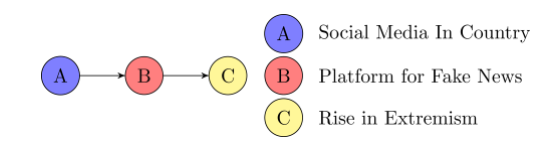
\(A \perp C \mid B\) ?
Mediator
Yes
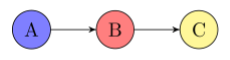
\(B \perp C \mid A\) ?
Confounder
Yes
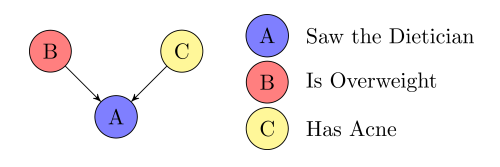
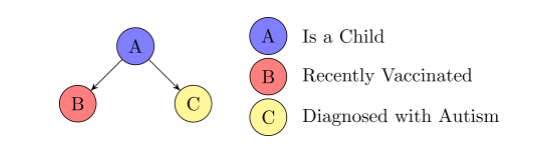
\(B \perp C \mid A\) ?
Collider
Inconclusive
https://kunalmenda.com/2019/02/21/causation-and-correlation/
More Complex Example
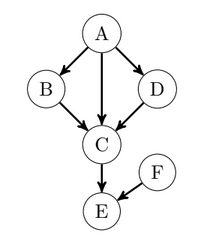
\((B\perp D \mid A)\) ?
\((B\perp D \mid E)\) ?
Yes!
No
Today: Systematic way to reason about conditional independence
Why is this relevant?
d-Separation
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\)
Let \(\mathcal{C}\) be a set of random variables.
A path between \(A\) and \(B\) is d-separated by \(\mathcal{C}\) if any of the following are true
We say that \(A\) and \(B\) are d-separated by \(\mathcal{C}\) if all paths between \(A\) and \(B\) are d-separated by \(\mathcal{C}\).
If \(A\) and \(B\) are d-separated by \(\mathcal{C}\) then \(A \perp B \mid \mathcal{C}\)
Next year: No *descendant* in C (see book)
Proving Conditional Independence
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\)
- Enumerate all paths between nodes in question
- Check all paths for d-separation
- If all paths d-separated, then CE
Example: \((B \perp D \mid C, E)\) ?

Exercise

\(D \perp C \mid B\) ?
\(D \perp C \mid E\) ?
- The path contains a chain \(X \rightarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains a fork \(X \leftarrow Y \rightarrow Z\) such that \(Y \in \mathcal{C}\)
- The path contains an inverted fork (v-structure) \(X \rightarrow Y \leftarrow Z\) such that \(Y \notin \mathcal{C}\)
Sampling from a Bayesian Network
Given a Bayesian network, how do we sample from the joint distribution it defines?

- Topoligical Sort (If there is an edge \(A \rightarrow B\), then \(A\) comes before \(B\))
- Sample from conditional distributions in order of the topological sort
Analogous to Simulating a (PO)MDP