POMDPs in Aerospace and Autonomy

ACASX
Autonomous Driving

1. ACASX

TCAS

ACASX POMDP

State variables

Actions

Transitions

Observations: Noisy and quantized measurements of \(h\), \(\dot{h}_0\), \(\dot{h}_1\)

ACASX POMDP: Reward

ACASX: QMDP Solution

ACASX: Policy

ACAS X

POMDP Models

Optimization

Specification

ACASX

Safer (especially when pilots don't respond) and much fewer advisories.

2. Autonomous Driving

Sadigh, Dorsa, et al. "Information gathering actions over human internal state." Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference on. IEEE, 2016.

Schmerling, Edward, et al. "Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction." arXiv preprint arXiv:1710.09483 (2017).

Sadigh, Dorsa, et al. "Planning for Autonomous Cars that Leverage Effects on Human Actions." Robotics: Science and Systems. 2016.

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

Human Behavior Model: IDM and MOBIL

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]

g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).

A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).

A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).

POMDP Formulation

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states of other cars

Actions filtered so they can never cause crashes
Braking action always available

Efficiency

Safety

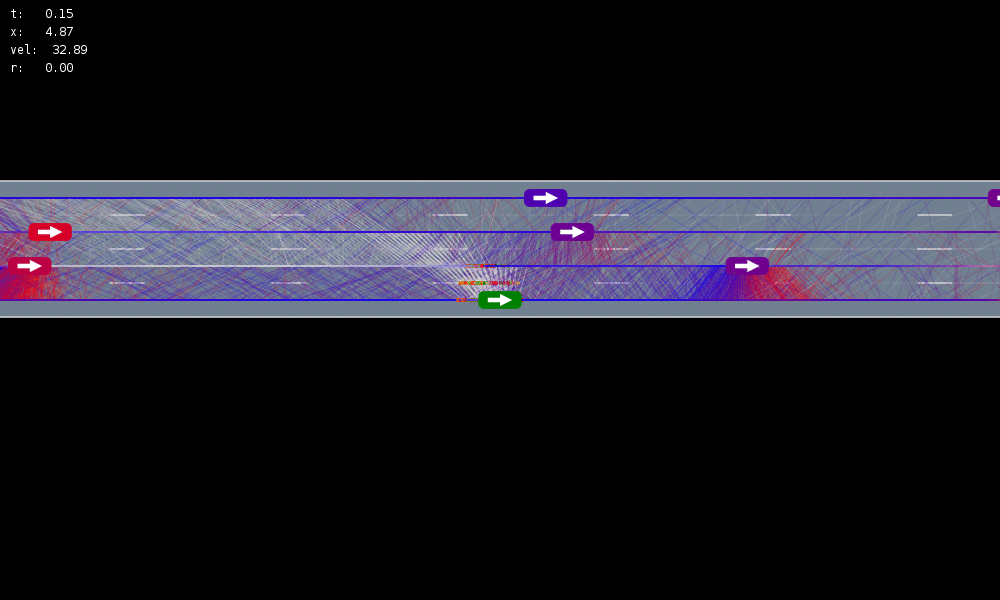
All drivers normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Simulation results

Assume normal

No Learning (MDP)

Omniscient

Mean MPC

QMDP

POMCPOW (Ours)

All drivers normal

Omniscient

Mean MPC

QMDP

POMCPOW