Online POMDP Methods
Approximate POMDP Solutions
Numerical Approximations
(approximately solve original problem)
Offline
Online
Formulation Approximations
(solve a slightly different problem)
Previously
Today!
Last Time
POMDP Sense-Plan-Act Loop
Environment
Option 2: Belief Updater
Policy
\(b\)
\(a\)
True State
\(s = TL\)
Observation \(o = TL\)
Belief: \(b_t = P(s_t \mid h_t)\)
\(TL\)
\(TR\)
(Options below)
Solver
Planner
Option 1: History
\(h\)
History: \(h_t = (b_0, a_0, o_1, a_1, \ldots a_{t-1}, o_{t})\)
Belief-Space Tree Search: AEMS
[Ross, et al., Online Planning Algorithms for POMDPs, 2008]
Next Year: Skip AEMS
Monte Carlo Tree Search (MCTS/UCT)
Search
Expansion
Rollout
Backup
\[Q(s, a) + c \sqrt{\frac{\log N(s)}{N(s,a)}}\]
low \(N(s, a)/N(s)\) = high bonus
start with \(c = 2(\bar{V} - \underline{V})\)
How should we adapt MCTS for POMDPs?
Environment
Policy
\(a\)
True State
\(s = TL\)
Observation \(o = TL\)
(Options below)
Option 1: History
\(h\)
History: \(h_t = (b_0, a_0, o_1, a_1, \ldots a_{t-1}, o_{t})\)
Option 2: Belief Updater
\(b\)
Belief: \(b_t = P(s_t \mid h_t)\)
\(TL\)
\(TR\)
MCTS on Histories


DESPOT

Somani, A., Ye, N., Hsu, D., & Lee, W. "DESPOT : Online POMDP Planning with Regularization." Journal of Artificial Intelligence Research, 2017
- Determinized Scenarios
- Guided by Lower and Upper Bounds
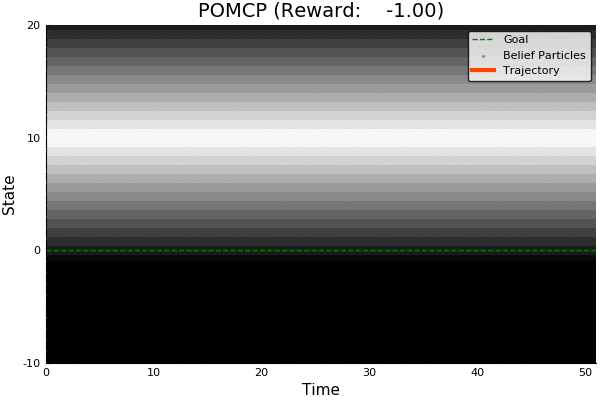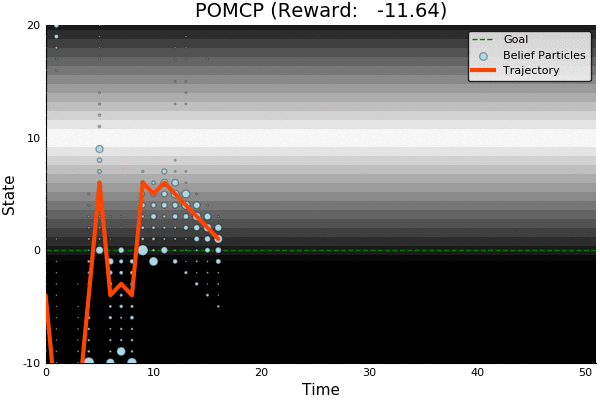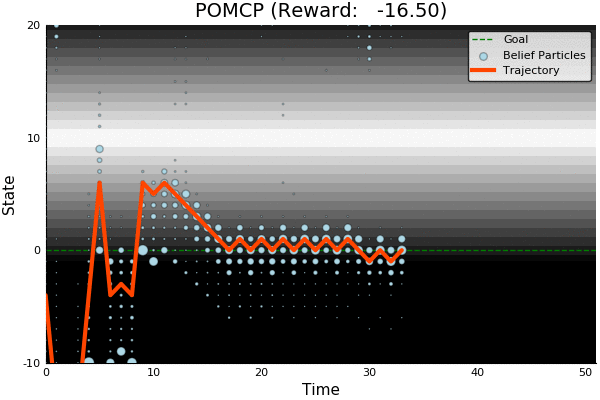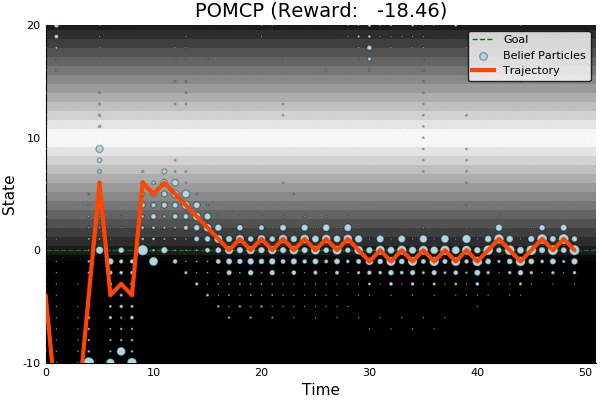


POMCP
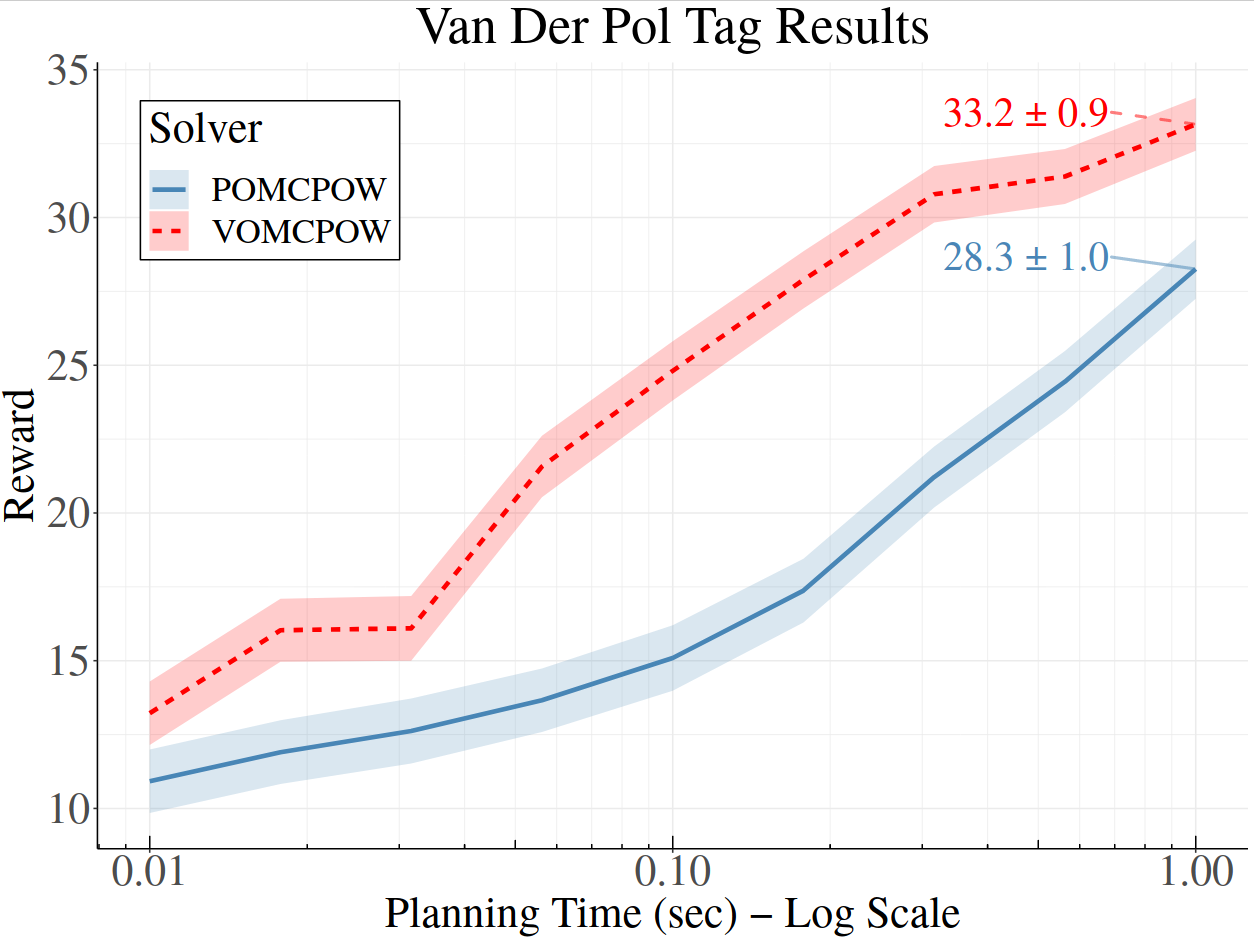
POMCPOW
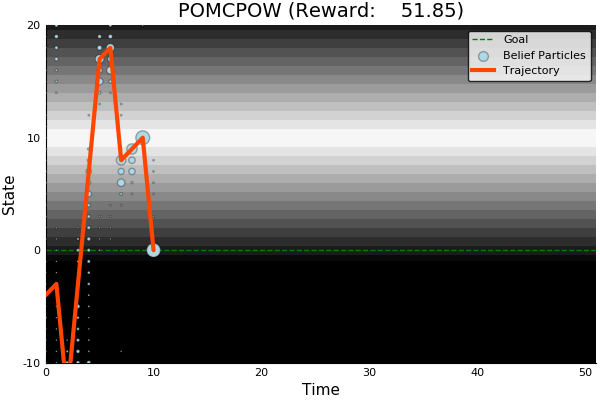
Continuous Observation Spaces
PF Approximation Accuracy
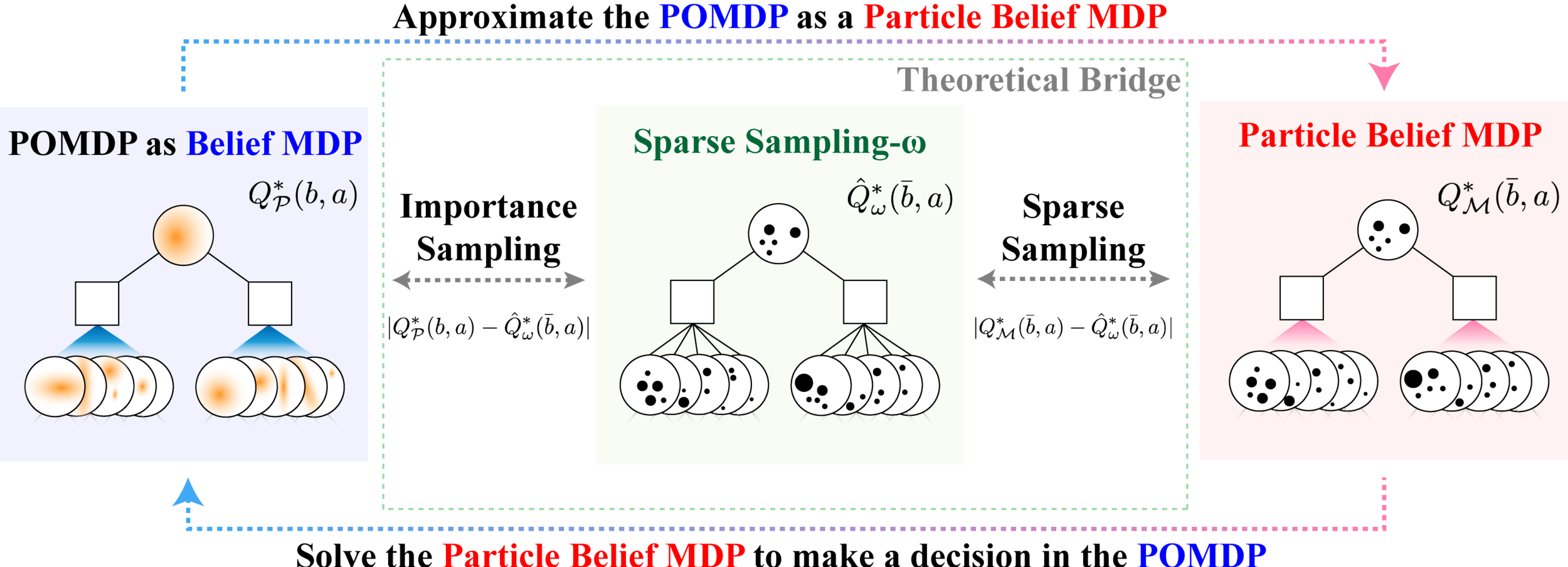
\[|Q_{\mathbf{P}}^*(b,a) - Q_{\mathbf{M}_{\mathbf{P}}}^*(\bar{b},a)| \leq \epsilon \quad \text{w.p. } 1-\delta\]
For any \(\epsilon>0\) and \(\delta>0\), if \(C\) (number of particles) is high enough,
\(\mathbf{M}_\mathbf{P}\) = Particle belief MDP approximation of POMDP \(\mathbf{P}\)
[Lim, Becker, Kochenderfer, Tomlin, & Sunberg, 2023]
No dependence on \(|\mathcal{S}|\) or \(|\mathcal{O}|\)!
DESPOT-\(\alpha\)
BOMCP


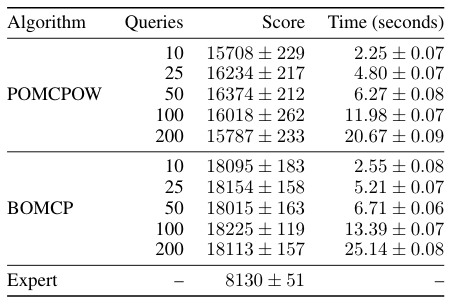
Continuous Action Spaces
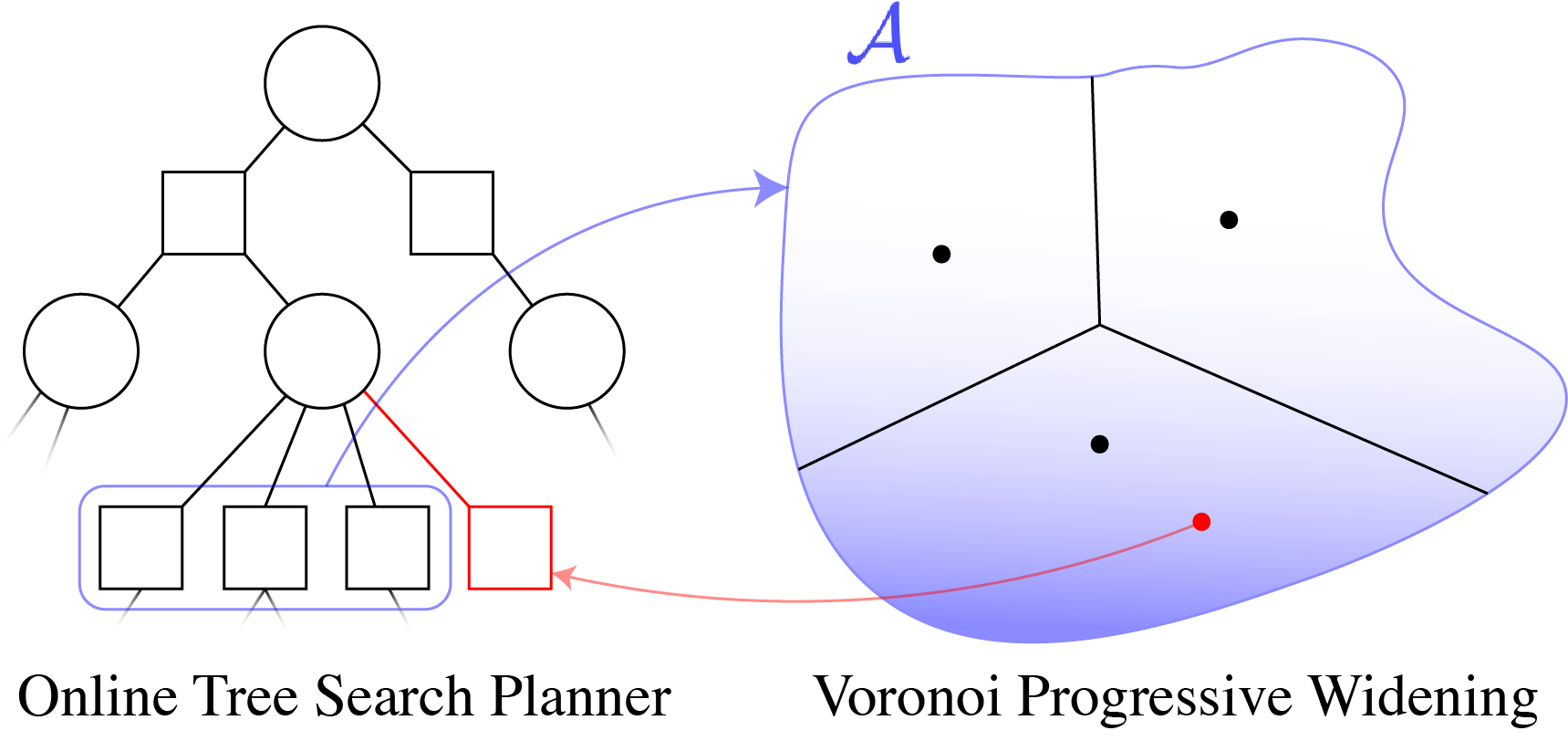
Voronoi Progressive Widening