Offline POMDP Algorithms
Last time: POMDP Value Iteration (horizon \(d\))
\(\Gamma^0 \gets \emptyset\)
for \(n \in 1\ldots d\)
Construct \(\Gamma^n\) by expanding with \(\Gamma^{n-1}\)
Prune \(\Gamma^n\)
Finite Horizon POMDP Value Iteration

Finite Horizon POMDP Value Iteration



Infinite-Horizon POMDP Lower Bound Improvement
\(\Gamma \gets\) blind lower bound
loop
\(\Gamma \gets \Gamma \cup \text{backup}(\Gamma)\)
\(\Gamma \gets \text{prune}(\Gamma)\)
Infinite-Horizon POMDP Value Iteration
\(\Gamma \gets\) blind lower bound
loop
\(\Gamma \gets \Gamma \cup \text{backup}(\Gamma)\)
\(\Gamma \gets \text{prune}(\Gamma)\)

Point-Based Value Iteration (PBVI)
point_backup\((\Gamma, b)\)
for \(a \in A\)
for \(o \in O\)
\(b' \gets \tau(b, a, o)\)
\(\alpha_{a,o} \gets \underset{\alpha \in \Gamma}{\text{argmax}} \; \alpha^\top b'\)
for \(s \in S\)
\(\alpha_a[s] = R(s, a) + \gamma \sum_{s', o} T(s'\mid s, a) \,Z(o' \mid a, s') \, \alpha_{a, o}[s']\)
return \(\underset{\alpha_a}{\text{argmax}} \; \alpha_a^\top b\)
Point-Based Value Iteration (PBVI)
function point_backup\((\Gamma, b)\)
for \(a \in A\)
for \(o \in O\)
\(b' \gets \tau(b, a, o)\)
\(\alpha_{a,o} \gets \underset{\alpha \in \Gamma}{\text{argmax}} \; \alpha^\top b'\)
for \(s \in S\)
\(\alpha_a[s] = R(s, a) + \gamma \sum_{s', o} T(s'\mid s, a) \,Z(o \mid a, s') \, \alpha_{a, o}[s']\)
return \(\underset{\alpha_a}{\text{argmax}} \; \alpha_a^\top b\)


Original PBVI
\(B \gets {b_0}\)
loop
for \(b \in B\)
\(\Gamma \gets \Gamma \cup \{\text{point\_backup}(\Gamma, b)\}\)
\(B' \gets \empty\)
for \(b \in B\)
\(\tilde{B} \gets \{\tau(b, a, o) : a \in A, o \in O\}\)
\(B' \gets B' \cup \left\{\underset{b' \in \tilde{B}}{\text{argmax}} \; \lVert B, b' \rVert\right\}\)
\(B \gets B \cup B'\)
Original PBVI

PERSEUS: Randomly Selected Beliefs
Two Phases:
- Random Exploration
- Value Backup
Random Exploration:
\(B \gets \emptyset\)
\(b \gets b_0\)
loop until \(\lvert B \rvert = n\)
\(a \gets \text{rand}(A)\)
\(o \gets \text{rand}(P(o \mid b, a))\)
\(b \gets \tau(b, a, o)\)
\(B = B \cup \{b\}\)
Heuristic Search Value Iteration (HSVI)
while \(\overline{V}(b_0) - \underline{V}(b_0) > \epsilon \)
explore\((b_0, 0)\)
explore(b, t)
if \(\overline{V}(b) - \underline{V}(b) > \epsilon \gamma^t\)
\(a^* = \underset{a}{\text{argmax}} \; \overline{Q}(b, a)\)
\(o^* = \underset{o}{\text{argmax}} \; P(o \mid b, a) \left(\overline{V}(\tau(b, a^*, o)) - \underline{V}(\tau(b, a^*, o)) - \epsilon \gamma^t\right)\)
explore(\(\tau(b, a^*, o^*), t+1\))
\(\underline{\Gamma} \gets \underline{\Gamma} \cup \text{point\_backup}(\underline{\Gamma}, b)\)
\(\overline{V}(b) = B_b \left[ \overline{V}(b) \right]\)
Heuristic Search Value Iteration

Sawtooth Upper Bounds
Sawtooth Upper Bounds

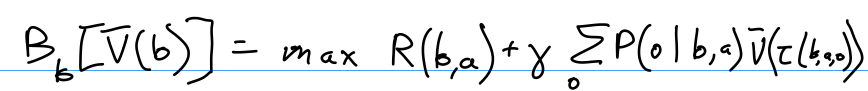
SARSOP
Successive Approximation of Reachable Space under Optimal Policies
SARSOP
Successive Approximation of Reachable Space under Optimal Policies


Offline POMDP Algorithms
Offline POMDP Algorithms

Policy Graphs
Policy Graphs

Monte Carlo Value Iteration (MCVI)

Monte Carlo Value Iteration (MCVI)


