Actor-Critic, Reward Shaping, Advanced Exploration, and Entropy Regularization
Map
Challenges:
- Exploration vs Exploitation
- Credit Assignment
- Generalization
- More Actor-Critic
- Advanced Exploration
- Entropy Regularization
- Wisdom
Actor-Critic
\[\nabla U(\theta) = E_\tau \left[\sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_{k,\text{to-go}}-r_\text{base}(s_k)) \right]\]
Advantage Function: \(A(s, a) = Q(s, a) - V(s)\)
- Actor: \(\pi_\theta\)
- Critic: \(Q_\phi\) and/or \(A_\phi\) and/or \(V_\phi\)
Can we combine value-based and policy-based methods?
Alternate between training Actor and Critic
Problem: Instability
Actor-Critic
Which should we learn? \(A\), \(Q\), or \(V\)?
\[\nabla U(\theta) = E_\tau \left[\sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_k + \gamma V_\phi (s_{k+1}) - V_\phi (s_k))) \right]\]
\(l(\phi) = E\left[\left(V_\phi(s) - V^{\pi_\theta}(s)\right)^2\right]\)
Generalized Advantage Estimation
\(A(s_k, a_k) \approx r_k + \gamma V_\phi (s_{k+1}) - V_\phi (s_k)\)
\(A(s_k, a_k) \approx \sum_{t=k}^\infty \gamma^{t-k} r_t\)
\(A(s_k, a_k) \approx \sum_{t=k}^{d-1} \gamma^{t-k} r_t + \gamma^{d-k} r_d + \gamma V_\phi (s_{d+1}) - V_\phi (s_d)\)
let \(\delta_t = r_t + \gamma V_\phi (s_{t+1}) - V_\phi (s_t)\)
\[A_\text{GAE}(s_k, a_k) \approx \sum_{t=k}^\infty (\gamma \lambda)^{t-k} \delta_t\]
Alpha Zero: Actor Critic with MCTS
- Use \(\pi_\theta\) and \(U_\phi\) in MCTS
- Learn \(\pi_\theta\) and \(U_\phi\) from tree

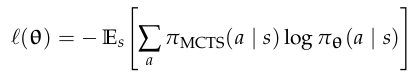



Reward Shaping


Which is easier to learn on?
Sparse Reward
Dense Reward
https://www.youtube.com/watch?v=tlOIHko8ySg
Coast Runners 7: A Cautionary Tale
Reward Shaping
"As a general rule, it is better to design performance measures according to what one actually wants in the environment, rather than according to how one thinks the agent should behave." - Stuart Russell


Reward
Value
Potential-Based Reward Shaping
- \(R'(s, a, s') = R(s, a, s') + \gamma \phi(s') - \phi(s)\)
- any other transformation may yield sub optimal policies unless further assumptions are made about the underlying MDP
Continuous Actions: Deep Deterministic Policy Gradient
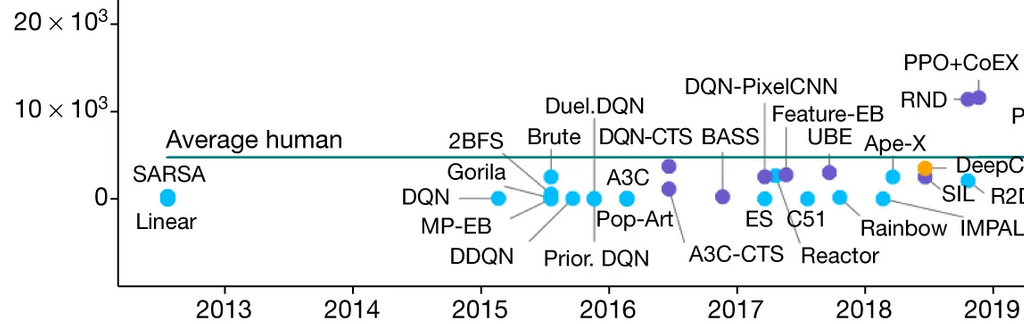
Is Exploration Important?
Montezuma's Revenge
Is Exploration Important?
Theory

Exploration Bonus
- In General, \(R^+(s, a) = R(s, a) + B(s, a)\)
- UCB: \(B(s, a) = c \sqrt{\frac{\log N(s)}{N(s, a)}}\)
Example 1: Learn Pseudocount
\(B(s, a) \approx \frac{1}{\sqrt{\hat{N}(s)}}\) where \(\hat{N}(s)\) is a learned function approximation



Bellemare, et al. 2016 "Unifying Count-Based Exploration..."
Exploration Bonus
Example 2: Learn a function of the state and action
\(B(s, a) = \lVert \hat{f}_\theta (s, a) - f^*(s, a) \rVert^2\)
What should \(f^*\) be?
- \(f^*(s, a) = s'\) (Next state prediction)
- \(f^*(s, a) = f_\phi (s, a)\) where \(f_\phi\) is a random neural network.
Exploration Bonus
Example 3: Thompson Sampling
- Maintain a distribution over \(Q\)
- Sample \(Q\)
- Act according to \(Q\)
- Bootstrapping with multiple \(Q\) networks
- Dropout
Exploration Bonus
Example 4: Go-Explore

"First return, then explore"

(Uber AI Labs)
Soft Actor Critic: Entropy Regularization
\[U(\pi) = E \left[\sum_{t=0}^\infty \gamma^t \left(r_t + \alpha \mathcal{H}(\pi(\cdot \mid s_t))\right)\right]\]



Soft Actor Critic





Soft Actor Critic
Advantages:
- Stable
- Learns many near-optimal policies
- Exploration
- Insensitivity to hyperparameters
- Off-Policy

Disadvantages
- Sensitive to \(\alpha\) Solution = Entropy *constraint* and adjust \(\alpha\)
Wisdom
Deep RL: The Dream

Using Deep RL for your problem
- Some interesting problem (smallsat swarm)
- Spend weeks theorizing about the exact-right cost function and dynamics
- Decide RL can solve all of your problems
- Fire up open-ai baselines
- Does it work??



Why not?
- Hyperparameters?
- Reward scaling?
- Not enough training time????
Algorithms

Policy Network Architecture



Reward Rescaling


"simply multiplying the rewards generated from an environment by some scalar"
Statistical Significance

"Unfortunately, in recent reported results, it is not uncommon for the top-N trials to be selected from among several trials (Wu et al. 2017; Mnih et al. 2016)"
Codebases


How to choose an RL Algorithm
(According to Sergey Levine)

Model-Based RL
Model-Based Deep RL
Off-Policy
Q-Learning
Actor Critic
On Policy Policy Gradient
Evolutionary/Gradient Free
(Most people use SAC or PPO)
How to be successful with RL
- Always start with a small problem that works and scale up (keep verifying that it works with every change)
- Plot everything that you can think of (TensorBoard)
- *Losses*
- Policies
- Value functions
- Trajectories
- (Average return) Learning curve
- Keep calm and lower your learning rate

Where Does RL Work?
- Cooling servers
- Winning at Go

