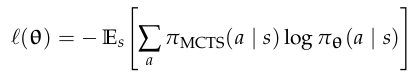DQN and Advanced Policy Gradient
Map
Map
Challenges:
- Exploration vs Exploitation
- Credit Assignment
- Generalization
Part I
DQN
Q-Learning with Neural Networks
Q-Learning:
\(Q(s, a) \gets Q(s, a) + \alpha\, \left(r + \gamma \max_{a'} Q(s', a') - Q(s, a)\right)\)
Neural Networks
\[\theta^* = \argmin_\theta \sum_{(x,y) \in \mathcal{D}} l(f_\theta(x), y)\]
\[\theta \gets \theta - \alpha \, \nabla_\theta\, l (f_\theta(x), y)\]
Deep Q learning:
- Approximate \(Q\) with \(Q_\theta\)
- What should \((x, y)\) be?
- What should \(l\) be?
Candidate Algorithm:
loop
\(a \gets \text{argmax} \, Q(s, a) \, \text{w.p.} \, 1-\epsilon, \quad \text{rand}(A) \, \text{o.w.}\)
\(r \gets \text{act!}(\text{env}, a)\)
\(s' \gets \text{observe}(\text{env})\)
\(\theta \gets \theta - \alpha\, \nabla_\theta \left( r + \gamma \max_{a'} Q_\theta (s', a') - Q_\theta (s, a)\right)^2\)
\(s \gets s'\)
DQN: The Atari Benchmark




DQN: Problems with Naive Approach
Candidate Algorithm:
loop
\(a \gets \text{argmax} \, Q(s, a) \, \text{w.p.} \, 1-\epsilon, \quad \text{rand}(A) \, \text{o.w.}\)
\(r \gets \text{act!}(\text{env}, a)\)
\(s' \gets \text{observe}(\text{env})\)
\(\theta \gets \theta - \alpha\, \nabla_\theta \left( r + \gamma \max_{a'} Q_\theta (s', a') - Q_\theta (s, a)\right)^2\)
\(s \gets s'\)
Problems:
- Samples Highly Correlated
- Size-1 batches
- Moving target
DQN
Q Network Structure:
Experience Tuple: \((s, a, r, s')\)
Loss:
\[l(s, a, r, s') = \left(r+\gamma \max_{a'} Q_{\theta'}(s', a') - Q_\theta (s, a)\right)^2\]
DQN
Q Network Structure:
Experience Tuple: \((s, a, r, s')\)
Loss:
\[l(s, a, r, s') = \left(r+\gamma \max_{a'} Q_{\theta'}(s', a') - Q_\theta (s, a)\right)^2\]






Rainbow
- Double Q Learning
- Prioritized Replay
(priority proportional to last TD error) - Dueling networks
Value network + advantage network
\(Q(s, a) = V(s) + A(s, a)\) - Multi-step learning
\((r_t + \gamma r_{t+1} + \ldots + \gamma^{n-1} r_{t+n-1} + \gamma \max Q_\theta(s_{t+n}, a') - Q_\theta(s_t, a_t))^2\) - Distributional RL
predict an entire distribution of values instead of just Q - Noisy Nets

Actual Learning Curves

Part II
Improved Policy Gradients
Restricted Gradient Update
\[\widehat{\nabla U}(\theta) = \sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_{k,\text{to-go}}-r_\text{base}(s_k)) \]
\[\theta' = \theta + \alpha \widehat{\nabla U}(\theta)\]


Restricted Gradient Update
\[\widehat{\nabla U}(\theta) = \sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_{k,\text{to-go}}-r_\text{base}(s_k)) \]
\[U(\theta') \approx U(\theta) + \nabla U(\theta)^\top (\theta' - \theta)\]
\(\underset{\theta'}{\text{maximize}}\)
\(\text{subject to}\)
\[g(\theta, \theta') = \lVert\theta-\theta'\rVert^2_2 = \frac{1}{2}(\theta' - \theta)^\top (\theta' - \theta)\]

\(\mathbf{u} = \nabla U(\theta)\)
\[\theta' = \theta + \alpha \widehat{\nabla U}(\theta)\]
\[g(\theta, \theta') \leq \epsilon\]

Natural Gradient
Natural Gradient







Natural Gradient

TRPO and PPO

TRPO = Trust Region Policy Optimization
(Natural gradient + line search)



PPO = Proximal Policy Optimization
(Use clamped surrogate objective to remove the need for line search)
Part III
Actor-Critic
Actor-Critic
Actor-Critic
\[\nabla U(\theta) = E_\tau \left[\sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_{k,\text{to-go}}-r_\text{base}(s_k)) \right]\]
Advantage Function: \(A(s, a) = Q(s, a) - V(s)\)
- Actor: \(\pi_\theta\)
- Critic: \(Q_\phi\) and/or \(A_\phi\) and/or \(V_\phi\)
Can we combine value-based and policy-based methods?
Alternate between training Actor and Critic
Problem: Instability
Actor-Critic
Which should we learn? \(A\), \(Q\), or \(V\)?
\[\nabla U(\theta) = E_\tau \left[\sum_{k=0}^d \nabla_\theta \log \pi_\theta (a_k \mid s_k) \gamma^{k} (r_k + \gamma V_\phi (s_{k+1}) - V_\phi (s_k))) \right]\]
\(l(\phi) = E\left[\left(V_\phi(s) - V^{\pi_\theta}(s)\right)^2\right]\)
Generalized Advantage Estimation
Generalized Advantage Estimation
\(A(s_k, a_k) \approx r_k + \gamma V_\phi (s_{k+1}) - V_\phi (s_k)\)
\(A(s_k, a_k) \approx \sum_{t=k}^\infty \gamma^{t-k} r_t - V_\phi (s_k) \)
\(A(s_k, a_k) \approx r_k + \gamma r_{k+1} + \ldots + \gamma^d r_{k+d} + \gamma^{d+1} V_\phi (s_{k+d+1}) - V_\phi (s_k)\)
let \(\delta_t = r_t + \gamma V_\phi (s_{t+1}) - V_\phi (s_t)\)
\[A_\text{GAE}(s_k, a_k) \approx \sum_{t=k}^\infty (\gamma \lambda)^{t-k} \delta_t\]
Recap
Alpha Zero: Actor Critic with MCTS
- Use \(\pi_\theta\) and \(U_\phi\) in MCTS
- Learn \(\pi_\theta\) and \(U_\phi\) from tree